Análisis de supervivencia

Resumen

El análisis de supervivencia es un método estadístico que valora el tiempo entre un evento inicial (inclusión del sujeto en el estudio) y uno final, que sucede cuando este presenta una característica definida con anterioridad (evento). Su objetivo es estimar, teniendo en cuenta la variable tiempo, la probabilidad de que ocurra un suceso determinado. Tiene la particularidad de aceptar tiempos incompletos de participación y asumir que todos los factores implicados en el estudio son homogéneos. Existen varios métodos para calcular la probabilidad de supervivencia; los más utilizados son los de Kaplan-Meier y el actuarial.

Abstract

Survival analysis is a statistical method that assesses the time between an initial event (inclusion of the subject in the study) and a final event, which occurs when the subject presents a previously defined characteristic. Its objective is to estimate, taking into account the time variable, the probability of a certain event occurring. It has the particularity of accepting incomplete participation times and assuming that all the factors involved in the study are homogeneous. There are several methods to calculate the probability of survival, the most used are the Kaplan-Meier and the actuarial.

En medicina se suele aplicar el análisis de supervivencia con el fin de valorar la supervivencia de los pacientes a una determinada enfermedad. Este tipo de estudios pertenecen a los llamados longitudinales, en los que los individuos se siguen a lo largo del tiempo; en este caso, el seguimiento se hace desde la entrada al estudio de un individuo hasta la ocurrencia de un evento de interés¹.

Este evento no es necesariamente la muerte, puede ser tiempo de recurrencia, tiempo que dura la eficacia de una intervención, tiempo de remisión, tiempo de persistencia de un tratamiento², tiempo de aparición de nuevos factores de riesgo en un seguimiento³, etc., lo que hace de estos estudios una herramienta muy útil en Atención Primaria. El vocablo supervivencia se debe a que en las primeras aplicaciones de este método de análisis se utilizaba como evento la muerte de un paciente.

Estos estudios están especialmente diseñados para determinar la probabilidad de un suceso en diferentes intervalos de tiempo, siendo siempre el intervalo de tiempo la variable dependiente. Además, en él pueden participar pacientes con tiempos incompletos que no han llegado al estadio terminal¹.

Conceptos básicos

• a)

  Fecha de inicio. Es aquella en que después de haber terminado los preparativos (protocolos, permisos, etc.), se empieza la inclusión de pacientes. Es igual para todos los pacientes.

• b)

  Fecha de entrada. Cuando se incorpora al paciente en el estudio. Es muy importante porque a partir de ella se calcula el tiempo de supervivencia. Es diferente para cada sujeto.

• c)

  Fecha de última observación. Última visita realizada. Tanto las fechas de entrada como de última observación son diferentes para cada paciente, puesto que estos se incorporan en diferentes momentos.

• d)

  Tiempo de participación. El tiempo transcurrido entre la fecha de entrada y la fecha de última observación.

• e)

  Fecha de cierre. Cuando se decide finalizar el estudio. Debe ser la misma para todos los pacientes.

• f)

  Duración del estudio. El intervalo de tiempo discurrido entre la fecha de entrada y la fecha de cierre.

• g)

  Tiempo de supervivencia. Se define como el intervalo de tiempo entre la entrada del paciente en el estudio y el evento de interés⁴.

• h)

  Paciente censurado. Cuando su tiempo de participación termina antes de la fecha de cierre y por consiguiente su seguimiento es incompleto o perdido. El tiempo de participación puede terminar por los siguientes motivos:

• 1.

  El paciente decide no participar más en el estudio y lo abandona.

• 2.

  El paciente se pierde (por ejemplo, cambia de domicilio) y no tenemos más información sobre él.

• 3.

  El estudio termina antes de aparecer el evento que estudiamos⁵ (fig. 1).

  
  

  Figura 1.

  Esquema del tiempo de supervivencia tras la entrada en un estudio. Tomado de Abraira¹.

  El estudio empezó el 1 de enero de 1990 y acabó el 1 de enero de 2002. En A el eje temporal representa años de calendario y en B años desde el diagnóstico. Con el círculo en blanco se representan los tiempos censurados y con el cuadrado negro las muertes (ocurrencia del evento). El individuo A al que se le diagnosticó en enero de 1990 desapareció del estudio en enero de 1993 (sería una censura a los 3 años por pérdida de seguimiento). El B, también diagnosticado en enero de 1990, falleció en junio de 1992 (muerte a los 2,5 años). El C seguía vivo al acabar el estudio (sería un dato censurado a los 12 años por fin del estudio). El D, al que se le diagnosticó en febrero de 1991, falleció en marzo de 1999; el tiempo de supervivencia sería de 8 años. El E, que fue diagnosticado en noviembre de 1993, falleció en accidente de tráfico en julio de 1997 (sería una muerte, o un dato censurado, a los 3,7 dependiendo de la definición de evento de interés). El F, al que se le diagnosticó al principio de 1996, seguía vivo al acabar el estudio (sería un dato censurado a los 6 años por fin del estudio).

Consideraciones importantes

Es necesario usar una definición operativa del punto de partida (operación quirúrgica, ingreso en el hospital, inicio de un tratamiento, etc.) para fijar la fecha de entrada en el estudio. No se deben usar situaciones ambiguas (por ejemplo, comienzo de sintomatología) que dependan de la memoria del paciente. Debe ser una fecha exacta.

El evento de interés debe ser claro y muy bien definido para poder precisar la fecha del mismo. En caso de ser la muerte del paciente, es imprescindible que esta sea como consecuencia de la enfermedad objeto del estudio. Si no es así, el fallecido debe valorarse como censurado y su tiempo de seguimiento como incompleto. En caso contrario estaremos introduciendo en el estudio un sesgo de información.

En la última observación es preciso registrar el estado del sujeto y la fecha de información de dicho estado. Si el evento de interés es la muerte y el paciente ha fallecido, calcularemos el tiempo de supervivencia en base a la fecha de defunción. Si el paciente está vivo a la fecha de la última observación, se calculará como tiempo incompleto o censurado, porque lo que define un tiempo completo es la presencia del evento de estudio.

De esta manera, podemos decir que los requisitos imprescindibles para disponer de datos idóneos para un análisis de supervivencia son⁵:

• 1.

  Definir adecuadamente el origen o inicio del seguimiento.

• 2.

  Definir adecuadamente la escala del tiempo.

• 3.

  Definir adecuadamente el evento de interés.

Sesgos. Tipos de observaciones

Los datos del estudio pueden estar sesgados por las censuras y los truncamientos. Como hemos visto anteriormente, en las censuras el tiempo de seguimiento termina antes de producirse el evento de interés o cuando este no se produjo.

En los truncamientos, se entró al estudio después del hecho que define el origen en todos los individuos analizados. Se tendría que haber empezado con anterioridad ya que la enfermedad habría comenzado antes.

De esta forma, se pueden producir cuatro tipos de observaciones de datos⁶:

• 1.

  No truncada, no censurada: el proceso se inicia en el inicio del seguimiento y el evento aparece durante el seguimiento realizado.

• 2.

  No truncada, censurada: el proceso se inicia en el inicio del seguimiento, pero el evento no aparece durante el seguimiento realizado.

• 3.

  Truncada no censurada: el paciente ya tenía el proceso cuando entró al estudio (lo hizo tarde) y el evento aparece durante el seguimiento realizado.

• 4.

  Truncada, censurada: el paciente ya tenía el proceso cuando entró al estudio y el evento no aparece durante el seguimiento realizado.

Supervivencia y riesgo

Los datos de supervivencia se pueden dar y estudiar con dos tipos de probabilidades diferentes: supervivencia y riesgo. La «probabilidad de supervivencia» (también llamada función de supervivencia) o S(t) es la probabilidad de que un individuo sobreviva desde la fecha de entrada en el estudio hasta un momento determinado en el tiempo t. Estos valores van a describir la supervivencia global de toda nuestra población. Esta función se centra sobre todo en la «no ocurrencia» del evento (el paciente no ha fallecido; o no ha recidivado) y se utiliza para encontrar la mediana (percentil 50) y otros percentiles de tiempo de vida, así como para comparar datos de supervivencia de dos o más grupos.

Pero más útil que la probabilidad de supervivencia es la «función de riesgo» h(t): que es la probabilidad de que a un individuo que está siendo observado en el tiempo t le suceda el evento en ese momento. Es decir: ¿cuál es la probabilidad de que fallezca un paciente con cáncer de pulmón microcítico a los 12 meses (suponiendo que haya sobrevivido hasta ese momento)? La función de riesgo se centra en la «ocurrencia» del evento y proporciona información como la tasa de incidencia, por ejemplo: ¿en qué momento voy a tener el pico de recidivas?⁷.

Análisis de datos

El análisis de datos para este tipo de estudios requiere métodos de análisis específicos debido a que frecuentemente se analizan los datos antes de que ocurra el evento terminal (si no el estudio duraría mucho tiempo), y por eso muchos de los datos que se poseen son censurados y además los pacientes no entran en el estudio al mismo tiempo.

Hay que tener en cuenta que en la mayor parte de los estudios la variable tiempo no tiene una distribución normal, más bien suele tener una distribución asimétrica, en la que típicamente tenemos más datos al principio que al final del período de seguimiento^1,8. En este caso suele utilizarse la prueba de Kaplan-Meier, aunque también existen otras pruebas no paramétricas como la de Log rango y la regresión de Cox^5,8.

Cuando la variable tiempo sigue una distribución normal, se pueden utilizar las pruebas de distribución exponencial, distribución de Weibull o distribución Log normal⁵.

Indudablemente los métodos estadísticos más utilizadas en el análisis de supervivencia son los de Kaplan-Meier y el actuarial⁹.

Método de Kaplan-Meier

Conocido también como del «límite del producto». En él suponemos que los sujetos censurados se habrían comportado del mismo modo que los seguidos hasta que se produjo el evento y asumimos que este evento terminal es independiente para cada paciente, lo que hace que las probabilidades de sobrevivir en un tiempo determinado se calculan gracias a una ley multiplicativa de probabilidades.

Aunque la supervivencia en un tiempo dado depende de la supervivencia en todos los períodos previos, la posibilidad de la misma en un período de tiempo es independiente de la probabilidad de supervivencia en los demás períodos. Otra característica distintiva es que no se agrupan los tiempos de supervivencia en intervalos. Debido a ello, este método es especialmente útil en estudios con un número pequeño de pacientes^5,6.

Método actuarial de Cutler-Ederer

Los tiempos de supervivencia se agrupan en intervalos. La longitud del intervalo depende de la frecuencia con que ocurre el evento de interés y puede no ser necesariamente de la misma longitud. La desventaja principal de este método es que da estimaciones poco precisas cuando el número de sujetos es pequeño. En muestras grandes, tiene una importancia fundamental porque influye poco sobre las estimaciones y además permite obtener una función de riesgo. Se asume que las retiradas y pérdidas se distribuyen homogéneamente en el intervalo, pero puede establecer un sesgo muy importante cuando los intervalos son muy grandes o hay muchos abandonos⁶.

Cálculo de las curvas de supervivencia en SPSS

Método de Kaplan-Meier

En un estudio de 62 pacientes con cáncer de pulmón, hemos estimado el tiempo de supervivencia de cada uno de ellos y hemos anotado su estado al final del seguimiento (el evento de interés era el fallecimiento) y el tipo celular del tumor que tenían. Los datos de estas variables los hemos codificado de la siguiente manera:

Tiempo de supervivencia en días

Estado - 1: fallecido; 0: censurado

Tipo de célula - 1: escamoso; 2: adenocarcinoma

Ejecución del programa

Analizar → Supervivencia → Kaplan-Meier. Posteriormente aparecerá una nueva ventana donde introduciremos, en la casilla «Hora», la variable Tiempo, y en la casilla «Estado», como su propio nombre indica, la variable estado en donde hemos registrado si se presentó el suceso de interés o fue un dato censurado.

Definir evento → Valor único (ponemos el código que le hemos asignado al evento de interés, que en nuestro caso es 1) → Continuar

Opciones → marcamos tablas de supervivencia, media y mediana de supervivencia y en gráficos: supervivencia, después Continuar → Aceptar

De este modo obtendremos (figs. 2 y 3):

• -

  Un resumen del procesamiento de casos: número total de intervinientes en el estudio, número de eventos de interés, número de censurados y porcentaje de estos últimos.

• -

  La tabla de supervivencia ordenada de menor a mayor por tiempos de supervivencia: hora (en este caso tiempo en días), estado, proporción acumulada de personas que sobreviven en el tiempo con su desviación típica, número de eventos acumulados y número de casos restantes.

• -

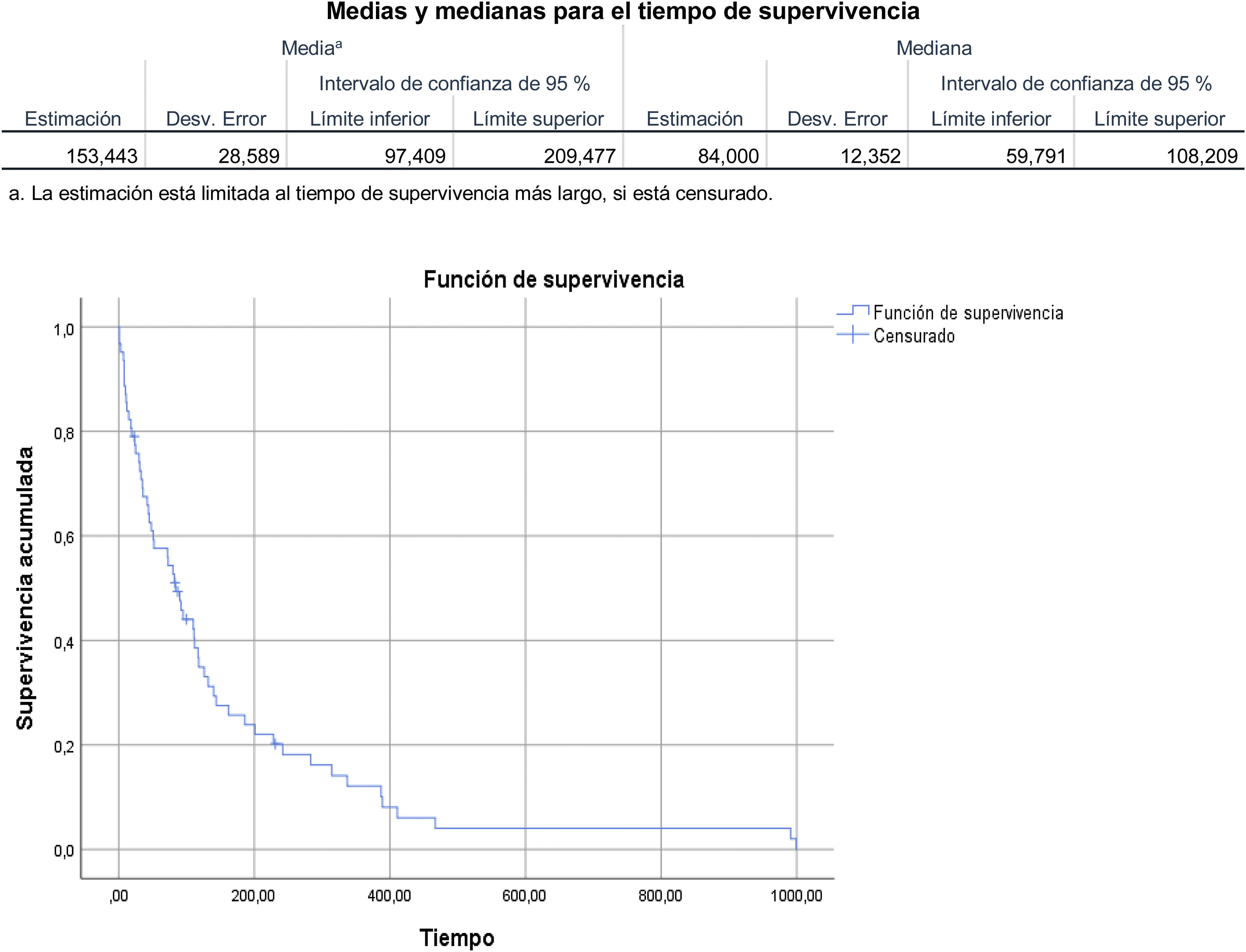
  Medias y medianas para el tiempo de supervivencia: estimación de la media y mediana con su desviación típica e intervalo de confianza al 95%.

• -

  Gráfico de la curva de supervivencia.

Figura 2.

Resumen de procesamiento de casos y tabla de supervivencia.

Figura 3.

Medias y medianas del tiempo de supervivencia y función de supervivencia.

Interpretación

Si observamos las columnas, hora (tiempo) y estimación de la tabla (fig. 2), podemos determinar la probabilidad de que una persona viva según el intervalo de tiempo que queramos averiguar. Así, podemos decir que en el primer mes (30 días) existe una probabilidad del 74,1% de supervivencia, del 47,6% a los 3 meses (90 días) y de algo más de un 10,1% al año.

Por otra parte, al tratarse de una distribución paramétrica de datos es preferible utilizar la mediana (percentil 50) a la media, para precisar cuál es el tiempo de supervivencia del 50% de la población estudiada. La media es una medida que describe la tendencia central de una distribución, sin embargo, en este caso es más adecuado usar la mediana por la menor influencia que ejercen en ella los valores extremos de la variable tiempo.

En este estudio el 50% de la población tenía un tiempo de supervivencia de 84 días (fig. 3). Respecto a la curva, esta representa un tiempo de supervivencia corto.

Comparación de dos curvas

Si en nuestro estudio además queremos saber en cuál de los dos tumores (escamoso y adenocarcinoma) es mayor el tiempo de supervivencia, tenemos que comparar las curvas de supervivencia de cada uno de ellos.

Para ello seguimos el mismo procedimiento que en el apartado anterior, es decir: Analizar → Supervivencia → Kaplan-Meier, a continuación introduciremos en la casilla «Hora» la variable Tiempo y en la casilla «Estado», la variable estado. Después: Definir evento → Valor único (ponemos el código que le hemos asignado al evento de interés) → Continuar

Pero en esta ocasión: Factor (introducimos la variable por la cual queremos saber si hay diferecia entre las curvas de supervivencia, que en nuestro caso es Tipo) → Comparar factor → Log rango → Continuar

Opciones → marcamos tablas de supervivencia, media y mediana de supervivencia y en gráficos: supervivencia, después Continuar → Aceptar

De esta manera obtendremos (fig. 4):

• -

  Medias y medianas para el tiempo de supervivencia de ambos tumores con sus desviaciones típicas e intervalos de confianza al 95%.

• -

  Prueba de Log rango (Mantel-Cox) para determinar si hay diferencias significativas entre las dos variables.

• -

  Gráfico de las dos curvas de supervivencia.

Figura 4.

Comparación entre dos curvas de supervivencia.

Interpretación

Al analizar los resultados, observamos que hay una gran diferencia en lo que se refiere a tiempos de supervivencia entre la media de los tumores escamosos y los adenocarcinomas a favor de los primeros. Al aplicar el estadístico Log rango (Mantel-Cox), apreciamos que esta diferencia entre las dos curvas de supervivencia es estadísticamente muy significativa (p < 0,001), por lo cual tenemos que rechazar la hipótesis nula que establecía que no había diferencias entre ambas, lo que significa que los pacientes con tumores de tipo escamoso tienen mayor esperanza de vida que los que tienen adenocarcinoma.