El coeficiente de correlación intraclase permite medir la concordancia general entre dos o más mediciones que implican variables de carácter cuantitativo, obtenidas estas con diferentes instrumentos de medida o evaluadores. Se basa en un modelo de análisis de varianza con medidas repetidas. Su uso solo es posible si existe normalidad de las distribuciones de las variables, igualdad de varianzas e independencia entre los errores producidos por los observadores.
The intraclass correlation coefficient makes it possible to measure the general concordance between two or more measurements that involve variables of a quantitative nature, obtained with different measuring instruments or evaluators. It is based on an analysis of variance model with repeated measures. Its use is only possible if there is normality of the distributions of the variables, equality of variances and independence between the errors produced by the observers.
En el ámbito clínico en ocasiones es necesario valorar la fiabilidad de las mediciones u observaciones realizadas. En este sentido podemos diferenciar dos circunstancias: a)valorar la fiabilidad de los resultados obtenidos cuando repetimos la medición con el mismo instrumento y en condiciones idénticas, y b)evaluar esta fiabilidad cuando obtenemos los resultados con diferentes instrumentos de medida o con diferentes observadores1.
Cuando se mide, siempre habrá un cierto error que dependerá de forma aleatoria de variables como el instrumento, la manipulación, el sujeto evaluado, etc. Cualquier medición es el resultado de sumar el valor real de aquello que queremos medir y un error aleatorio.
Un instrumento fiable será aquel cuyo error aleatorio sea lo suficientemente pequeño como para que nos permita considerar que el resultado obtenido no es atribuible a errores en la medición2.
En el caso de variables cualitativas, los índices kappa y kappa ponderado han demostrado ser los estadísticos más adecuados para estimar la fiabilidad en distintas mediciones3, y cuando se trata de variables cuantitativas continuas se debe utilizar para hacer esta evaluación el coeficiente de correlación intraclase (CCI)4.
En numerosas ocasiones se cometen errores al valorar la fiabilidad de las mediciones repetidas en casos de variables cuantitativas, al recurrir al uso del coeficiente de correlación de Pearson (r)5. Como podemos observar en la tabla 1, en donde se comparan dos mediciones consecutivas de la presión arterial sistólica en 10 pacientes, realizadas con el mismo esfigmomanómetro por dos médicos diferentes, la r es excelente (0,95); sin embargo, la medición del médicoB es constantemente superior a la del médicoA. Esto se debe a que este coeficiente r lo que evidencia es la intensidad de la asociación lineal entre dos variables, es decir, su grado de asociación, pero no nos indica a qué se debe la diferencia sistemática entre las mismas, a favor de una de ellas, es decir, su grado de concordancia.
Medidas consecutivas de la presión arterial sistólica en 10 pacientes, realizadas por dos médicos con el mismo esfigmomanómetro
| Paciente | Médico A | Médico B |
|---|---|---|
| (mmHg) | (mmHg) | |
| 1 | 135 | 140 |
| 2 | 140 | 145 |
| 3 | 130 | 135 |
| 4 | 145 | 150 |
| 5 | 140 | 145 |
| 6 | 150 | 160 |
| 7 | 140 | 145 |
| 8 | 135 | 140 |
| 9 | 140 | 145 |
| 10 | 135 | 145 |
Fuente: Prieto et al.1.
Por este motivo, el uso del coeficiente de Pearson puede constituir una fuente de error en la medición, ya que omite en el cálculo la variabilidad intrasujeto e intersujeto, exponiendo al investigador a errores sistemáticos en sus interpretaciones5.
Con el objeto de soslayar este obstáculo, se utiliza el CCI, el cual se basa en el modelo de análisis de la variancia con medidas repetidas6. Mide el grado de concordancia entre medidas cuya varianza puede ser debida a5:
- •
Variabilidad intersujeto debida a la diferencias entre estos (σ2s).
- •
Variabilidad intrasujeto, debida a las diferencias de las mediciones de un mismo sujeto (σ2j).
- •
Variabilidad residual, es inexplicable (aleatoria), va unida a los errores de medición (σ2e).
El CCI es el cociente entre la varianza de los sujetos y la varianza total (varianza intersujeto, más varianza intrasujeto, más varianza residual):
CCI = (σ2s) / (σ2s) + (σ2j) + (σ2e)
Se define como la proporción de variabilidad total debida a la variabilidad de los sujetos1.
Al aplicar el método se pueden obtener valores comprendidos entre 0 y 1, donde 0 significa ausencia de concordancia y 1, concordancia o fiabilidad absoluta. De manera convencional se admiten los siguientes valores7:
- •
< 0,40: Pobre.
- •
0,40-0,59: Suficiente.
- •
0,60-0,74: Bueno.
- •
0,75-1: Excelente.
Para que se pueda usar el CCI es necesario que se cumplan las siguientes condiciones: que exista normalidad de las distribuciones de las variables, homocestacidad (igualdad de varianzas) e independencia entre los errores producidos por los observadores1.
Una limitación del CCI es que depende de la variabilidad de los valores observados. Si los pacientes varían poco en sus mediciones (muestra homogénea), el CCI tiende a ser bajo, ya que compara la varianza entre pacientes con la varianza total observada. Si la muestra es heterogénea, el CCI propende a ser mayor1.
Como alternativa al CCI se puede utilizar el método de Bland y Altman, que consiste en representar gráficamente, en un diagrama de dispersión, la media de las dos mediciones como la mejor estimación del verdadero valor, frente a la diferencia absoluta entre los dos valores. El gráfico incluye, además, una línea horizontal en la diferencia media y dos líneas, llamadas límites de concordancia, a una distancia de 1,96 desviaciones estándar por arriba y por debajo de la primera. Si las diferencias entre los pares de observaciones siguen aproximadamente una distribución normal y los valores tienden a ser estables en todo el rango de medición, se espera que el 95% de esas diferencias caigan dentro de los límites de concordancia. Esto permite valorar gráficamente, de forma sencilla, el grado de acuerdo entre los dos métodos8.
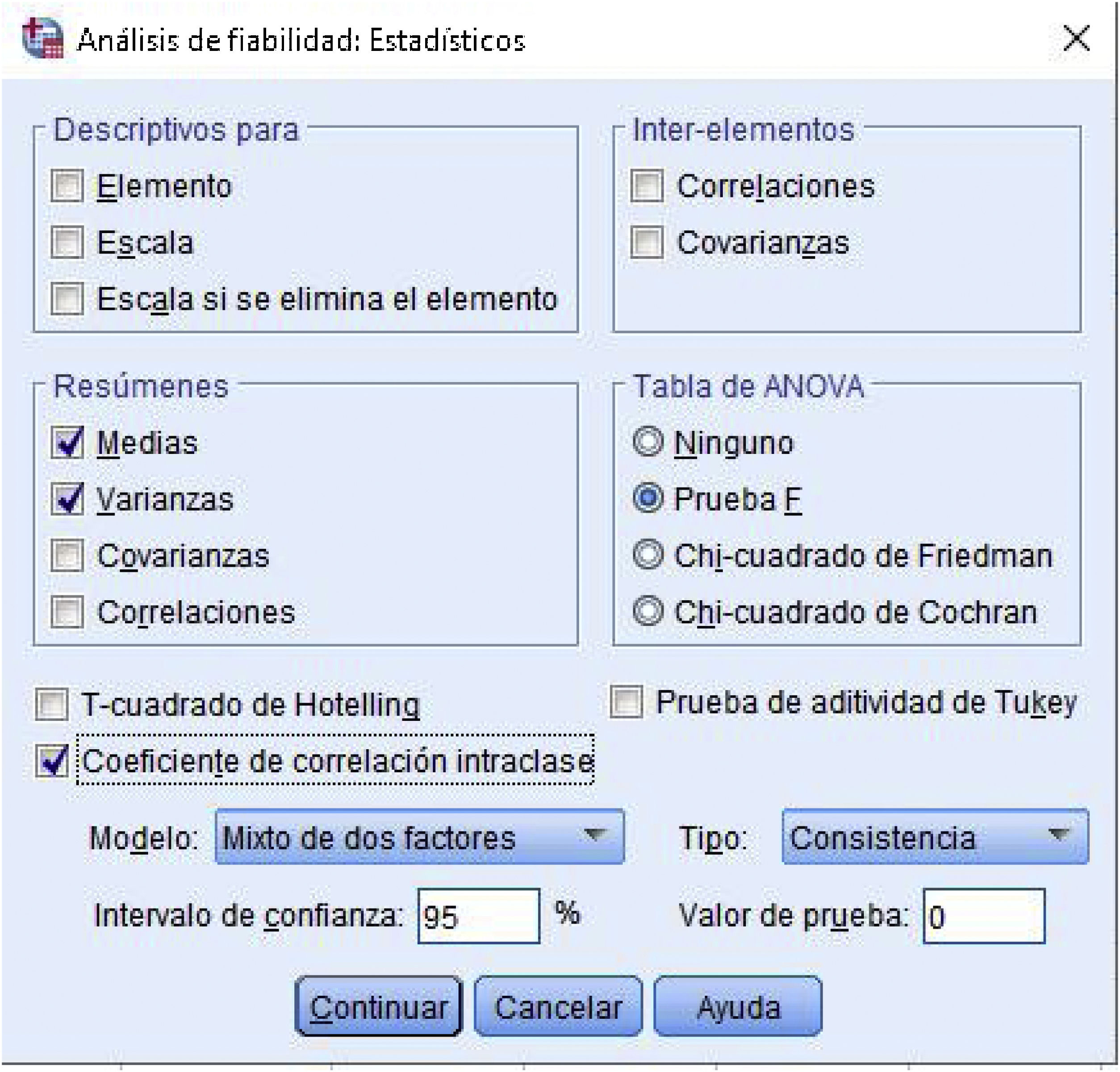
Cálculo del CCI en SPSSSeleccionar en los menús: Analizar → Escala → Análisis de fiabilidad → (aquí elegimos las variables que vamos a valorar) → Estadísticos → Coeficiente de correlación intraclase → Modelo, Tipo (fig. 1) → Continuar → Aceptar: obtención de los valores del coeficiente de correlación intraclase (fig. 2).
En primer lugar debemos distinguir entre modelo de efectos aleatorios y modelo de efectos fijos. En el primero los observadores implicados en la medición, por ejemplo los médicosA yB, representan una «muestra» aleatoria de la población de posibles observadores (p.ej., otros médicos del centro de salud) que en el futuro harán uso del instrumento evaluado.
En el modelo de efectos fijos, los observadores que intervienen en el estudio son los únicos que participan en el mismo.
En este módulo tenemos que elegir una de las tres siguientes opciones:
- •
Mixto de dos factores. Se usa cuando los médicos son de efectos fijos y los pacientes son de efectos aleatorios (el más utilizado).
- •
Aleatorio de dos factores. Se emplea cuando tanto los sujetos como los evaluadores son de efectos aleatorios.
- •
Aleatorio de un factor. Esta opción se usa cuando los efectos de las personas son aleatorios y no tenemos en cuenta la influencia de los evaluadores. Por ejemplo, tomamos dos medidas sin importar el orden en el cual se han realizado, bien porque lo desconozcamos o bien porque seamos totalmente conscientes de que no influyen en el resultado de nuestro experimento2. Es el menos usado.
Hay que elegir una de las dos siguientes alternativas:
- •
Consistencia. Se emplea en el caso de que, aunque el promedio de los valores de las medidas de los dos instrumentos estén asociados linealmente, existen diferencias constantes entre ellos en la medida persona a persona.
- •
Acuerdo absoluto. Se utiliza cuando los dos instrumentos miden los mismos valores.
En la figura 2 podemos observar que al aplicar el programa informático obtenemos el CCI, con su intervalo de confianza del 95%, y también el estadístico de prueba Anova para medidas repetidas (F) con su significación estadística. Este estadísticoF es útil para valorar si existe sesgo (error sistemático) en la medición realizada7.
Los resultados figuran en función de si en el estudio solo participaba un observador (medidas únicas) o más de uno, en cuyo caso se expone la media de todos los observadores (medidas promedio). La mayor parte de las veces nos interesan estas últimas, aplicando las medidas individuales solo en aquellas situaciones en que queremos saber cuán preciso es un evaluador único al evaluar los valores obtenidos en su medición.
Como vemos en el ejemplo, el CCI logrado es de 0,94 y su rango se sitúa entre el 0,83 y el 0,98, lo cual nos indica que la concordancia en la medición entre los dos instrumentos evaluados es excelente.
Consideraciones éticasEl trabajo no implicó el uso de sujetos humanos.
FinanciaciónEl trabajo no contó con apoyo financiero.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.