Todas las investigaciones clínicas se realizan en un grupo determinado de individuos, generalmente pacientes. Sin embargo, el interés del estudio radica, habitualmente, en la generalización de los resultados: no se está tan interesado en lo que ocurre con los individuos particulares que participan en la investigación como en predecir lo que pueda ocurrir en el futuro con otros individuos similares. Esto plantea dos problemas, el primero es el del sesgo de selección1, es decir, hasta qué punto los pacientes incluidos en el estudio son similares o, en la terminología estadística, pertenecen a la misma población que aquel o aquellos a quienes se quieren aplicar los resultados del estudio o, dicho de otra manera, hasta qué punto son tan distintos como para que los resultados del estudio no sean útiles para tomar las decisiones sobre éstos2. El segundo problema es que los estudios nunca se realizan con todos los pacientes de interés, sino sólo con un grupo de ellos o, en terminología estadística, no se trabaja con la población sino con una muestra. La estadística sirve justamente para solucionar este segundo problema con las técnicas de estimación y contraste de hipótesis3.
Por ejemplo, en un estudio para evaluar la eficacia de los inhaladores de nicotina para reducir la cantidad de tabaco fumado4 se definió como éxito en cada individuo que, en el período comprendido entre la sexta semana y el cuarto mes desde el inicio del tratamiento, se redujera al menos en un 50% el número de cigarrillos fumados diariamente. Los participantes en el estudio fueron 400 voluntarios sanos, reclutados por anuncios en los periódicos, que estaban dispuestos a reducir su consumo de tabaco, pero no a dejar de fumar inmediatamente, o eran incapaces de ello. Los participantes fueron distribuidos aleatoriamente en dos grupos de 200, la evaluación de la eficacia se obtuvo de la comparación de las proporciones de éxito entre los grupos tratado (26%) y placebo (9%) y se pretende que este resultado sea aplicable a otros fumadores. En el artículo se describen las características demográficas de los participantes y las de su historia y hábito tabáquico para ayudar al lector a juzgar cuán diferentes puedan ser de otros fumadores a quienes se quiera aplicar el tratamiento (sesgo de selección). Una vez aceptado que son suficientemente parecidos, el siguiente problema es cuánto tienen que ver las proporciones de éxito del 26 y el 9% obtenidas en los 200 individuos concretos que participan en cada grupo del estudio (muestra) con las proporciones respectivas en todos los individuos (población) a los que sea aplicable y cuánto dependen estas proporciones de que se obtengan en 200, 20 o 2.000 individuos.
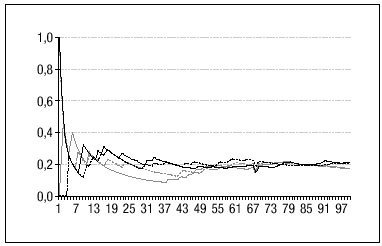
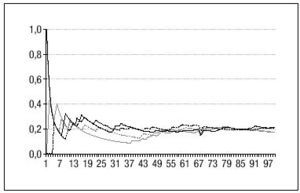
Para ayudar a comprenderlo pensemos en otro problema similar: ¿cuál es la probabilidad de que al tirar un dado salga un dos? La diferencia entre ambos problemas reside en que en este último, si aceptamos que el dado está bien construido, podemos calcular que la probabilidad es 1/6, cálculo que no se puede realizar para el éxito de los inhaladores de nicotina. Sin embargo, también podríamos resolver el problema del dado tirándolo una serie de veces y calculando la proporción de veces en que sale el dos. En la figura 1 se ilustra la evolución de esta proporción en función del número de tiradas en 4 series. En ella se observa la característica forma de embudo correspondiente a una ley empírica que dice que la proporción oscila, pero que la amplitud de las oscilaciones va decreciendo a medida que aumenta el número de tiradas, de tal modo que en todas las series tiende a estabilizarse en el mismo valor, a pesar de que obviamente también es posible que en alguna serie salga el dos en todas las tiradas o no salga en ninguna. Se puede definir la probabilidad de un suceso como el valor en el que se estabiliza la proporción de veces en que el suceso ocurre. El problema consiste en saber, en cada caso, si el "número de tiradas" es suficientemente grande para que la proporción se haya estabilizado. Es decir, volviendo al estudio de los inhaladores, ¿el número de fumadores estudiados es suficiente para que las proporciones de éxito en cada grupo ya estén estabilizadas cerca de las verdaderas probabilidades de éxito? o, planteado de otra manera, dado el número de fumadores estudiados y las proporciones de éxito encontradas, ¿dentro de qué intervalo estarían las verdaderas probabilidades de éxito?
Figura 1. Evolución de la proporción del resultado "dos" en función del número de "tiradas" del dado en 4 series de 100 "tiradas" (los valores finales de las 4 series varían en este caso entre 0,17 y 0,21).
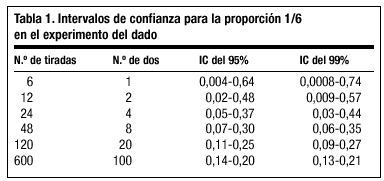
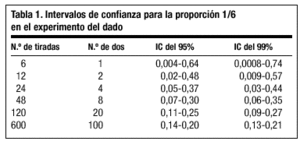
Imaginemos que no sabemos si el dado está bien construido o está "cargado", es decir, no sabemos si la probabilidad de que salga un dos es realmente 1/6 (= 0,166). El experimento para estudiarlo consiste en tirar el dado varias veces. Supongamos que lo tiramos 6 veces y el dos sale en una ocasión. En este punto la mejor estimación de la probabilidad del dos es la proporción 1/6, pero está claro que, con tan sólo 6 tiradas, esta proporción puede estar muy alejada de la probabilidad y sería perfectamente posible encontrar este resultado con un dado cargado. En función de experiencias similares a la representada en la figura 1 se podría aceptar que la verdadera probabilidad podría estar en un amplio intervalo como, por ejemplo, 0,005 y 0,7. Piénsese, o constrúyase con un poco de paciencia, una gráfica como la de la figura 1 para el resultado "cara" en varias series de tiradas de una moneda. En la zona izquierda, las partes anchas de los embudos se solaparían. Si tiramos ahora el dado 24 veces y encontramos el dos en 4 ocasiones la mejor estimación sigue siendo 4/24 = 1/6, pero el intervalo de probabilidades se estrecharía, digamos que entre 0,05 y 0,35. Si lo tiramos 120 veces y el dos se obtiene en 20 ocasiones, la estimación continúa siendo 20/120 = 1/6, pero el intervalo se habría estrechado aún más, por ejemplo entre 0,1 y 0,2. Estos intervalos se denominan "intervalos de confianza" y las técnicas estadísticas permiten construirlos de una forma precisa y fiable, asumiendo que la muestra del estudio es una muestra aleatoria de la población de interés. En la tabla 1 se incluyen los intervalos para el problema del dado, construidos con un nivel de confianza del 95 y el 99%.
Esta tabla ilustra cómo los intervalos de confianza nos indican si el tamaño de una muestra es suficiente para contestar a una pregunta de investigación. Si deseamos estar razonablemente seguros de que la "carga" del dado no altera la probabilidad del dos en más del 10% necesitamos menos de 120 tiradas, pero si queremos asegurar un error menor del 3% necesitaríamos 600.
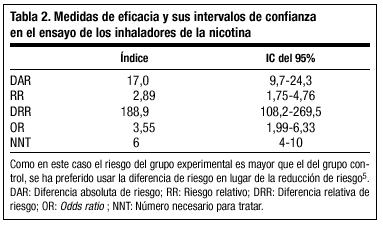
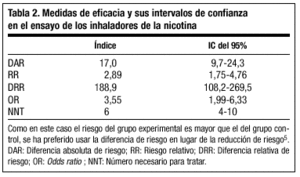
En el caso de los inhaladores de nicotina los intervalos de confianza del 95% para el placebo son del 5,4-13,9%, y para el grupo tratado del 20,1-32,7%; que ambos no se solapen nos está indicando que el tamaño muestral es suficientemente grande para estar seguros, con un 95% de confianza, de que las proporciones de éxito son verdaderamente distintas en ambos grupos. Las técnicas estadísticas permiten construir intervalos de confianza no sólo para las proporciones sino también para todas las medidas del efecto de un tratamiento vistas en notas previas5,6, y siempre debería darse el intervalo de confianza del índice usado. En la tabla 2 aparecen los distintos índices y sus intervalos de confianza para el ensayo de los inhaladores de nicotina.
Correspondencia: Dr. V. Abraira.Unidad de Bioestadística Clínica. Hospital Ramón y Cajal.Ctra. Colmenar, km 9,100. 28034 Madrid.
Correo electrónico: victor.abraira@hrc.es