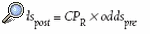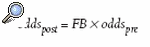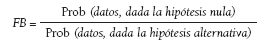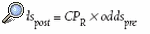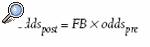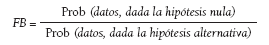En la nota dedicada a los contrastes de hipótesis1 se señalaba que la interpretación errónea más frecuente que se hace de ellos, en los artículos publicados en las revistas médicas, consiste en interpretar el valor p como la probabilidad de que la hipótesis nula sea cierta y que, por lo tanto, un resultado "significativo", es decir, un resultado para el que el valor p sea pequeño, significa que es muy improbable que la hipótesis nula sea cierta. Seguramente este error es tan frecuente porque ésta es la interpretación con la que los investigadores se sienten más cómodos, la que resulta más fácil e intuitiva. El problema es que no es correcta: recordemos que el valor p es la probabilidad del resultado obtenido, u otro más alejado de la hipótesis nula, si la hipótesis nula fuera cierta. Es una medida de la discrepancia de los datos con la hipótesis, pero no es la probabilidad de que la hipótesis sea cierta, ya que se ha calculado aceptando que lo sea.
Para comprender bien esa diferencia, hay que entender el concepto de probabilidad condicionada que concierne a un suceso bajo el supuesto de la verificación de otro2. Por ejemplo, si la incontinencia anal afecta al 2,2% de la población general, pero al 60% de los ancianos institucionalizados3, la probabilidad de que un individuo cualquiera la padezca es 0,022, pero si el individuo es un anciano internado en una residencia, la probabilidad de que la padezca es 0,6. Es decir, el hecho de que ocurra un suceso, en este caso ser un anciano institucionalizado, puede cambiar la probabilidad de otro, en el ejemplo, padecer incontinencia fecal. A esta última probabilidad se le denomina probabilidad condicionada del segundo suceso (incontinencia) condicionada a, o dado, el primero (ser anciano institucionalizado). El cambio en la probabilidad condicionada, respecto a la probabilidad sin condicionar, es tanto mayor cuanto más relacionados están los sucesos. El proceso de realizar la historia clínica, explorar y realizar pruebas complementarias para diagnosticar una enfermedad es un ejemplo de uso de este principio. Los clínicos, buscan (anamnesis), o provocan (pruebas diagnósticas) los sucesos que, dado que han ocurrido, más puedan cambiar la probabilidad de la posible enfermedad que están considerando. En general, los médicos lo hacen de forma intuitiva, pero el cambio de la probabilidad de un suceso incierto (padecer una determinada enfermedad), debido a la ocurrencia de otros sucesos relacionados (síntomas o resultados de pruebas diagnósticas) se puede formalizar mediante el teorema de Bayes. Una de las formas más sencillas de este teorema se vio en la nota dedicada a los índices de rendimiento de las pruebas diagnósticas4 y es:
Recuérdese que se denomina odds al cociente entre la probabilidad de que un evento (en este caso "estar enfermo") ocurra y la probabilidad de que no ocurra. Los subíndices post y pre indican posprueba, o condicionado al resultado de la prueba, y preprueba, respectivamente y CPR es el cociente de probabilidad del resultado de la prueba. Como se vio entonces con un ejemplo4, para interpretar, con este formalismo, el resultado de una prueba diagnóstica, se debería estimar, por su sintomatología e historia, la probabilidad de que el paciente tenga la enfermedad y se deberían conocer los CP de los posibles resultados de la prueba, para que, una vez conocido el resultado, se pueda aplicar la fórmula anterior para obtener la probabilidad condicionada a este resultado.
De modo similar se puede aplicar este formalismo al contraste de hipótesis. En este caso, también interesa ver cómo los datos observados en el estudio cambian la probabilidad, no de estar enfermo, sino de la hipótesis en evaluación. La fórmula anterior se suele representar como:
donde los odds son, ahora, los de la hipótesis nula y, en lugar del CP, el denominado factor de Bayes (FB) que, aunque en este contexto cambia de nombre, tiene la misma forma, es decir:
Nótese que con esta forma de hacer la inferencia, el resultado es el odds. A partir del odds se puede fácilmente calcular la probabilidad4 de que la hipótesis nula sea cierta dados los datos observados, que como se dijo antes, es la interpretación que los investigadores tienden a dar erróneamente al valor p de los contrastes de hipótesis. Podríamos pensar, por ello, que es la forma más natural e intuitiva de expresar los resultados de la inferencia y, por lo tanto, es ésta la primera ventaja del método basado en el teorema de Bayes con respecto al método convencional.
Otra ventaja importante del método bayesiano es que permite, a través del oddspre, incorporar al proceso inferencial los resultados procedentes de estudios previos. Recuérdese que la imposibilidad de hacerlo es una de las críticas más importantes al método convencional1. Sin embargo, esta incorporación se ha señalado también como una debilidad del método, como una puerta abierta a la subjetividad del investigador, puesto que el investigador incorpora su grado de convicción, siempre subjetivo, acerca de la hipótesis en evaluación. Los defensores del método bayesiano recuerdan que subjetivo no es sinónimo de caprichoso y argumentan que es inevitable que los investigadores tengan sus convicciones sobre las hipótesis que evalúan y que, de un modo u otro, siempre las incorporan. Más vale, por lo tanto, que lo hagan explícitamente, con un método que lo permite formalmente y que, por ello, hace posible un "análisis de sensibilidad", es decir el examen de las modificaciones que distintas convicciones puedan provocar en el resultado final6. En todo caso, esta incorporación del conocimiento previo sí parece ser una dificultad del método, ya que la mayoría de los investigadores que lo usan optan por usar el denominado precedente plano, o no informativo6 y que consiste en asignar a la hipótesis una probabilidad previa uniformemente repartida entre 0 y 1.
La forma habitual de usar este método consiste5 en expresar la probabilidad a priori como una distribución de probabilidad o, dicho de manera muy poco rigurosa, como un rango de valores posibles en el intervalo (0-1). La probabilidad, después del experimento, se expresa también como una distribución. Ambas, generalmente, representadas de forma gráfica. Existe, sin embargo, otra aproximación al método7 que resalta el hecho de que el teorema de Bayes tiene dos componentes, uno que incorpora la apreciación de conocimientos previos y otro, el FB, que resume la información contenida en los datos. Se puede decir que el FB es el índice a través del cual "hablan" los datos y está separado de la parte subjetiva de la ecuación. Si se tienen dificultades con la incorporación de la probabilidad a priori, se puede comunicar como resultado de la inferencia simplemente el FB, del mismo modo que en un estudio de evaluación de pruebas diagnósticas se comunican los CP. El FB, a diferencia del valor p, no es una probabilidad, sino un cociente de probabilidades, que compara dos hipótesis respecto a su capacidad para predecir los datos y que puede usarse tanto en la inferencia como en la toma de decisiones. Si, por ejemplo, en un ensayo clínico que compara dos tratamientos, en el que la hipótesis nula es que no hay diferencia entre ellos, se encuentra que FB=1/2, este resultado se puede interpretar de tres maneras:
1) Los resultados observados son la mitad de probables bajo la hipótesis nula que bajo la alternativa.
2) Los resultados avalan la hipótesis nula con la mitad de fuerza que la alternativa, o equivalentemente, avalan la hipótesis alternativa con el doble de fuerza que la nula.
3) Los resultados reducen el odds de la hipótesis nula a la mitad respecto al odds previo al ensayo. Esta interpretación es la que permite cuantificar la probabilidad de la hipótesis nula después del experimento, si se tiene una valoración previa.
Hasta ahora el uso de los métodos bayesianos en las revistas médicas es muy minoritario. Seguramente debido, al menos en parte, a la falta de herramientas adecuadas para hacer los cálculos necesarios, ya que los paquetes estadísticos más difundidos no las incorporan. Sin embargo, ya empieza a haber programas fáciles de usar que los incluyen. Uno de ellos, EPIDAT, en español y que contiene una ayuda muy didáctica, puede descargarse desde la dirección de Internet: http://dxsp.sergas.es/. Hay también una tendencia emergente entre los editores de revistas médicas a fomentar interpretaciones bayesianas de los resultados de las investigaciones8,9 que presumiblemente aumentará la cantidad de artículos que lo hagan, lo que obligará a los médicos a familiarizarse con estos métodos. Esta nota pretende modestamente contribuir a su difusión.