Obstetricia Estimación de peso fetal mediante regresión múltiple no lineal en el Hospital General Universitario de Alicante

PROGRESOS DE OBSTETRICIA Y GINECOLOGÍA

Volumen 41 Número 8 Octubre 1998

ARTÍCULOS ORIGINALES

Obstetricia

---

Estimación de peso fetal mediante regresión múltiple no lineal en el Hospital General Universitario de Alicante

Estimation of fetal weight by non-linear multiple regression at the General University Hospital of Alicante. Spain

M. Reíllo Flokrans ¹

L. Luque Martínez ²

J. C. Martínez Escoriza ³

M. Sanmartín Moreno ²

C. Bascuñana Martínez ²

Servicio de Obstetricia y Ginecología

Hospital General Universitario de Alicante

¹ Antiguo Residente

² Médico Interno Residente

³ Jefe del Servicio

Correspondencia:

Dr. Juan Carlos Martínez Escoriza

Jefe del Servicio de Obstetricia y Ginecología

Avda. Alonso Cano, 109

Alicante

Aceptado para publicación 15/4/98

Reíllo Flokrans M, Luque Martínez L, Martínez Escoriza JC, Sanmartín Moreno M, Bascuñana Martínez C. Estimación de peso fetal mediante regresión múltiple no lineal en el Hospital General Universitario de Alicante. Prog Obstet Ginecol 1998;41:450-457.

---

RESUMEN

Presentamos un método de cálculo de estimación de peso fetal mediante regresión no lineal múltiple partiendo de una selección de 645 partos de un total de 35.072 nacimientos correspondientes al período comprendido entre enero de 1986 y noviembre de 1996 del Hospital General Universitario de Alicante. La fórmula obtenida para el cálculo del peso en función de la edad gestacional (expresada como días totales de gestación dividido por siete) es la siguiente: peso = 24,5 + EXP{9,758367956 ­ 0,511792321* (edad gestacional) + 0,021548283* (edad gestacional)² ­ 0,000244240* (edad gestacional)³}. La R² fue de 0,911. Para desviación estándar la expresión es la siguiente: peso = (­ 1090,423896) + 69,100084174* (edad gestacional) ­ 0,791534162* (edad gestacional)². Con una R² de 0,728. La validación de la prueba se hizo con 660 casos, siendo la sensibilidad (S) y la especificidad (E) para casos extremos (menor de percentil 5 y mayor de percentil 95) de 86,0% y 94,9%, respectivamente.

PALABRAS CLAVE

Peso al nacimiento; Edad gestacional.

ABSTRACT

We have made a fetal weight estimation using a non-lineal regression. We used a selection of 645 deliveries of a total of 35,072 ones during the period from January 1986 to November 1996 at the «Hospital General Universitario de Alicante». We obtained the following formula of weight as a function of gestacional age (expressed as pregnancy days divided by seven): Weight = 24.5 + EXP {9.758367956 ­ 0.511792321* (pregnancy age) + 0.021548283* (pregnancy age)² ­ 0.000244240* (pregnancy age)³}. With a R² of 0.911. The formula for Standard Desviation was the following: Weight = (­1090.423896) + 69.100084174* (pregnancy age)­ 0.791534162* (pregnancy age)². With a R² of 0.728. Validation was made with 660 cases. We obtained a Sensibility of 86.0% and a Specificity of 94.9% in the ability of detecting extreme cases (lower than 5th percentile and higher than 95th percentile).

KEY WORDS

Birth weight; Pregnancy age.

---

INTRODUCCIÓN

La utilidad de conocer el peso fetal estriba fundamentalmente en la identificación de los recién nacidos de bajo peso. La encuesta nacional de morbimortalidad perinatal realizada por la Sección de Medicina Perinatal de la Sociedad Española de Obstetricia y Ginecología (SEGO) sobre un total de 469.545 nacidos estableció un índice de fetos de bajo peso (menor de 2.500 g) del 5,7% y un índice de fetos pretérmino de 6,8%. En aquel estudio se observó que el 68% de la mortalidad perinatal correspondía al grupo de bajo peso. Otros estudios han corroborado de la misma manera la mayor morbimortalidad en dicho grupo con diferencias significativamente estadísticas.

Diversos factores como sexo, raza, situación geográfica, estatus socioeconómico, gestación múltiple, talla baja constitucional, etc., y, cómo no, la metodología aplicada para clasificar los pesos influyen decisivamente en los resultados de estimación de peso fetal hasta tal punto que un recién nacido puede ser considerado normal no siéndolo, según las tablas aplicadas y viceversa.

El método más simple para la obtención de una curva de crecimiento consiste en estudiar los pesos fetales semana por semana, obteniendo sus estadísticos más habituales (método estadístico descriptivo). Otros más avanzados pasan por la obtención de una fórmula que exprese el peso en función de la edad gestacional. En el trabajo que aquí presentamos hemos pretendido elaborar, mediante combinación de diversas fórmulas matemáticas, un perfil más ajustado que correlacione peso-edad gestacional atendiendo a días de gestación y no a semanas como es habitual en las tablas de pesos. Permite elaborar las propias curvas de peso-edad gestacional a partir de una muestra seleccionada de un número no excesivo de casos. La finalidad de nuestra fórmula es la identificación de casos extremos que podrán ser estudiados en base a factores epidemiológicos y/o patológicos a posteriori.

MATERIAL Y MÉTODOS

Hemos realizado una búsqueda retrospectiva de los pesos al nacimiento de los recién nacidos de gestaciones no múltiples en el Hospital General Universitario de Alicante, según datos que obran en los libros de partos durante el período comprendido entre enero de 1986 y noviembre de 1996 con un total de 35.072 partos. El área de Alicante comprende una población de algo más de 200.000 personas, siendo, asimismo, hospital de referencia obstétrico de la provincia, con una población de 1.380.000 habitantes. De modo habitual las gestantes con previsión de parto con edades gestacionales comprendidas entre las semanas 24 a 32 de toda la provincia nos son remitidas. Muchos de estos casos no están exentos de patología fetal y/o materna, por lo que existen dos poblaciones diferentes entre los recién nacidos en nuestro hospital. Esta situación, obviamente, puede hacer variar el peso esperado, para un feto determinado, en una semana de gestación concreta.

Las características de las gestantes seleccionadas fueron las siguientes: mujeres mediterráneas, en su mayoría afincadas en la provincia de Alicante, con una media de edad de 28,7 años, una mediana de 29 y una moda de 30 años, el rango de edad fue de 14 a 46 años. La media de la paridad fue 1,8, con una mediana de 2 y una moda de 1, con una paridad máxima de 12.

Aunque inicialmente nuestra pretensión fue seleccionar 60 casos por semana de gestación partiendo en sentido retrospectivo desde los registros de noviembre de 1996, nos encontramos con la «dificultad» de no alcanzar dicho número de casos en edades gestacionales por debajo de la semana 30. Además, por debajo de la semana 29 el máximo obtenido no alcanzó los 40 casos en el período estudiado, por lo que para homogeneizar la muestra decidimos utilizar como línea de corte 40 casos. La muestra seleccionada para las semanas 34 a 42 se obtuvo con facilidad en el primer año de búsqueda. La razón de la homogeneidad deseada es inherente al método matemático utilizado.

La edad gestacional se introdujo en la base de datos especificando semana y día, siendo calculada por FUR o por ecografía del primer trimestre. Dado que en el libro de partos las semanas exactas no se acompañaban de día cero y observando que dicha «terminación» suponía más del 40% de los casos, cuando por ley probabilística debería corresponder aproximadamente a un 14% (1/7) de ellos, atribuimos la falta de aleatoriedad a la «relajación» en la precisión de la edad gestacional en dichos registros. Por ello y, en la medida de lo posible, se han seleccionado aquellos casos con semana y día distinto de cero, ejemplo: 38 semanas y cuatro días, ya que presumimos su mayor exactitud.

Se han desechado, de entrada, todo registro «absurdo» (edad gestacional coincidente con edad materna y peso incongruente), equívoco (grafías dudosas) y en una segunda fase de selección aquellas con semana gestacional superior a 42 + 3 por estar notoriamente fuera de protocolo de finalización de embarazo, considerándolos no controlados. Obtuvimos de este modo una muestra de 677 casos. Partiendo de dicha selección realizamos un análisis de la varianza obteniendo la media y la desviación estándar por semana (ANOVA). Para cada dato se calculó el valor de Z (número de desviaciones estándar con relación a la media). A continuación realizamos una regresión múltiple no lineal mediante tres fórmulas diferentes (fórmula de crecimiento de Rossavik ⁽¹⁾, método polinómico de tercer grado y una modificación de la fórmula sigmoide). Para cada fórmula se obtuvo la correspondiente R² (0,853; 0,863 y 0,854, respectivamente); dado que la mayor R² se consiguió mediante el método polinómico, elegimos éste para calcular la curva de la media de los valores según su fórmula. Comparamos dicha media con la obtenida por ANOVA para cada edad gestacional, esto nos sirvió para «depurar» casos extremos («outsiders»). Los criterios de depuración de datos se aplicaron para conseguir una distribución normal para cada edad gestacional y para la curva global de pesos. De esta forma, por semana, un valor de Z >= 1,96 (que corresponde a un percentil 95) se debía producir en un 5% de los casos, máxime si la fórmula polinómica estimaba que la media de dicha semana era superior a la esperada. Asimismo fueron tomadas en cuenta las fluctuantes desviaciones estándar, de tal modo que nuestra conducta depuradora fue más conservadora para semanas cuya desviación estándar (DE) era pequeña. De este modo se desestimaron 34 casos, quedando la muestra reducida a 643 casos.

Tras la depuración de datos se procedió a la regresión múltiple no lineal para calcular la media de pesos por edad gestacional. La máxima R² (0,91099) se obtuvo del logaritmo neperiano del peso en función de una ecuación de tercer grado de la edad gestacional fraccionada (por ejemplo: la semana 40 + 2 días se transforma en 40,2857142). A continuación hubo que sumar una constante a cada peso (24,5 g = suma de residuos de los pesos respecto de la media) para equipararla al valor real de la media (atribuimos este «fenómeno» a la «pérdida» en el transcurso de la obtención de logaritmos-antilogaritmos. Esto no sucedía si no se aplicaba dicha operación).

La distribución del peso en función de la edad gestacional sigue una distribución heterocedástica, es decir, la desviación estándar va aumentando progresivamente cuanto mayor es la edad gestacional. De forma ortodoxa, para elaborar el cálculo de los percentiles deberíamos transformar dicha distribución en homocedástica (DE constante). En nuestro caso y debido a las mayores fluctuaciones de desviación estándar que atribuimos a los fetos remitidos (con posible patología) de otros hospitales no pudimos obtener la homocedasticidad, por lo que optamos por un procedimiento «heterodoxo» consistente en «redefinir» la desviación estándar con respecto a la edad gestacional calculada por fórmula, elaborando posteriormente una regresión no lineal múltiple de la desviación estándar. Por ello, y siguiendo el método estadístico, la desviación se definió como la diferencia entre el peso real para cada caso y el valor teórico que le correspondería tener por fórmula. Del mismo modo, la varianza se definió como el sumatorio de todas las desviaciones elevado al cuadrado y dividido por el número de casos menos uno de cada semana. Por último, la desviación estándar para cada semana se obtuvo de la raíz cuadrada de la varianza. Si bien no se consiguió una desviación estándar constante sí que obtuvimos valores más uniformes. De esta forma elaboramos una nueva base de datos que incluía edad gestacional y desviación estándar sobre la que realizamos una regresión no lineal múltiple de segundo orden.

Dado que la muestra fue depurada y que utilizamos un método heterodoxo para calcular la desviación estándar realizamos la validación de la función con 660 casos nuevos no seleccionados. Determinamos la sensibilidad, especificidad, valor predictivo positivo y valor predictivo negativo de la fórmula para detectar fetos en los valores extremos ( < p 5 y > p 95 y para < p 10 y > p 90). Asimismo obtuvimos las curvas ROC para los percentiles 5-95 y 10-90. El valor de los percentiles «patrón» se calculó mediante una nueva base que incluía los casos del estudio sin depurar y los casos a validar, obteniendo mediante un procedimiento estadístico descriptivo (método Haverage) los percentiles teóricos.

Los procedimientos expuestos se repitieron por sexo.

Los datos fueron introducidos con el programa Epi Info versión 5 y exportados en formato Dbase III. La base de datos para calcular la desviación estándar fue generada mediante la hoja de cálculo Excell 3.1, siendo los análisis realizados con el paquete estadístico SPSS versión 5.1.

RESULTADOS

En la tabla 1 se expone:

* El peso esperado para una edad gestacional determinada (expresada como semanas fraccionadas, por ejemplo: semana 40 + 2 días es igual a 282 días; semana 40 + 2 dividido entre 7 es igual a 282 dividido entre 7 y esto es igual a 40,2857142) y que se obtiene mediante la fórmula: peso = 24,5 + EXP {9,7583 ­ ­ 0,511792321* (edad gestacional) + 0,021548283* (edad gestacional)² ­ 0,000244240* (edad gestacional)³} (donde EXP es antilogaritmo neperiano). La R² de la regresión fue de 0,91099.

* La desviación estándar para una edad gestacional dada se obtiene mediante la fórmula: peso = = (­ 1090,423896) + 69,100084174* (edad gestacional) ­ ­ 0,791534162* (edad gestacional)². La R² fue de 0,72871.

* Ambas medidas se diferenciaron también por sexos.

Tabla 1 Fórmulas para obtención de pesos en el Hospital General Universitario de Alicante
Estimación de pesos: Fórmulas para su cálculo en función de edad gestacional fraccionada (EG = días de gestación dividido por 7)
Pesos globales
Media de peso		R^2 = 0,91099
Peso = 24,539 + e^y;
y = (9,758367956 ­ 0,511792321*EG + 0,021548283*EG^2­ 0,000244240*EG^3)
Desviación estándar		R^2 = 0,72871
Peso = ­ 1090,423896 + 69,100084174*EG ­ 0,791534162*EG^2
Sexo femenino
Media de peso		R^2 = 0,90893
Peso = 21,423 + e^y;
y = (6,520546529 ­ 0,224256281*EG + 0,013169371*EG^2 ­ 0,000164167*EG^3)
Desviación estándar		R^2 = 0,42256
Peso = ­ 1471,796952 + 96,166367090*EG ­ 1,263630630*EG^2
Sexo masculino
Media de peso		R^2 = 0,91357
Peso = 27,279 + e^y;
y = 11,310356004 ­ 0,652639001*EG + 0,025724091*EG^2 ­ 0,000284617*EG^3
Desviación estándar		R^2 = 0,80150
Peso = ­ 960,8954236 + 58,857649536*EG ­ 0,582572887*EG^2
Algoritmo para el cálculo de z
z = (peso real ­ peso esperado por fórmula) / desviación estándar esperada por fórmula

A título meramente informativo exponemos la figura 1 en la que aparece la distribución por percentiles de nuestra muestra que, como anteriormente se dijo, no debe extrapolarse a otra población y, en su parte inferior, la curva de pesos obtenida.

		P 2,5	P 5	P 10	P 25	P 50	P 75	P 90	P 95	P 97,5
Semana	N	z: ­2	z: ­1,645	z: 1,282	z: ­0,675	z: 0	z: 0,675	z: 1,282	z: 1,645	z: 2
22,00	2	491	508	525	553	584	616	644	661	678
23,00	6	475	503	532	581	635	689	738	767	795
24,00	12	473	513	553	621	697	773	841	881	921
25,00	17	486	537	588	675	771	867	953	1.005	1.055
26,00	22	516	577	639	743	858	974	1.077	1.140	1.200
27,00	19	564	634	706	826	960	1.094	1.214	1.286	1.357
28,00	35	631	711	792	928	1.079	1.230	1.366	1.447	1.526
29,00	32	719	807	897	1.047	1.215	1.382	1.532	1.622	1.710
30,00	38	828	924	1.022	1.186	1.369	1.551	1.715	1.813	1.909
31,00	37	960	1.063	1.169	1.345	1.542	1.738	1.915	2.020	2.124
32,00	39	1.112	1.222	1.335	1.523	1.733	1.942	2.130	2.243	2.353
33,00	37	1.285	1.401	1.520	1.719	1.941	2.162	2.361	2.480	2.596
34,00	38	1.475	1.597	1.722	1.930	2.163	2.395	2.604	2.728	2.850
35,00	40	1.677	1.805	1.935	2.152	2.394	2.636	2.854	2.984	3.111
36,00	36	1.887	2.019	2.153	2.379	2.629	2.880	3.106	3.240	3.372
37,00	38	2.095	2.231	2.370	2.602	2.861	3.119	3.351	3.490	3.626
38,00	36	2.293	2.433	2.575	2.813	3.078	3.343	3.581	3.724	3.863
39,00	39	2.470	2.612	2.758	3.001	3.271	3.541	3.785	3.930	4.072
40,00	39	2.614	2.758	2.906	3.153	3.428	3.703	3.950	4.098	4.242
41,00	40	2.714	2.860	3.009	3.260	3.538	3.816	4.066	4.216	4.362
42,00	38	2.759	2.906	3.057	3.309	3.590	3.870	4.123	4.273	4.421
42,86		2.748	2.896	3.048	3.301	3.583	3.864	4.118	4.269	4.417

Figura 1.Tabla de pesos obtenida mediante algoritmo de una muestra de población de recién nacidos en el Hospital General Universitario de Alicante. N representa el número de casos utilizados en dicha semana. En la columna semana se incluye la semana exacta («0» días). Si se desea comparar con otras tablas en las que semana es la media de valores entre semana exacta y semana más seis días se debería promediar el valor de peso con la siguiente semana.

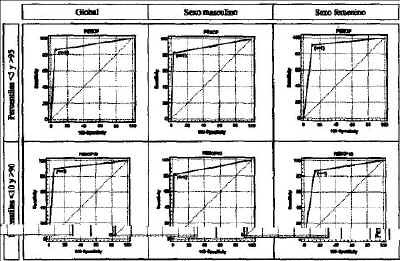
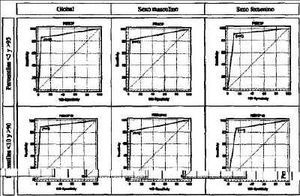
En la tabla 2 se exponen los resultados de la validación. Para la detección de casos muy extremos (percentiles 5 y 95), la sensibilidad de la fórmula aplicada a esta muestra fue 86,0% y la especificidad, 94,9%. El valor predictivo positivo fue 61,3% y el valor predictivo negativo, 98,6%. Puede apreciarse la alta especificidad que muestra la fórmula. El valor del área bajo la curva ROC corresponde, para el total de casos, a 0,904. En la figura 2 se muestran las curvas ROC para los percentiles extremos menor de 5 y mayor de 95 y para valores menores de 10 y mayores de 90.

Tabla 2 Valoración del algoritmo para cálculo de pesos extremos (5 y 10% de valores extremos altos y bajos). Destaca la elevada especificidad (es decir, su seguridad para diagnosticar niños normales)
		Total recién nacidos		Sexo femenino		Sexo masculino
		p < 5-> 95	p < 10-> 90	p < 5-> 95	p < 10-> 90	p < 5-> 95	p < 10-> 90
S		86,0%	89,7%	90,9%	87,0%	82,2%	81,8%
E		94,9%	93,5%	89,4%	86,5%	96,7%	97,6%
VPP		61,3%	76,4%	40,0%	58,0%	68,6%	88,5%
VPN		98,6%	97,5%	99,2%	96,9%	98,5%	96,0%
ROC		0,904	0,916	0,902	0,867	0,897	0,897
S: Sensibilidad; E: Especificidad; VPP: Valor predictivo positivo; VPN: Valor predictivo negativo; ROC: Área bajo la curva ROC.

Figura 2.Curvas ROC de la validación. Las curvas ROC se diseñaron durante la Segunda Guerra Mundial y permiten una valoración visual de la sensibilidad y la especificidad. Cuanto más cercano esté el punto de inflexión al ángulo superior izquierdo tanto mejor es un algoritmo.

Para finalizar hemos querido mostrar la correlación porcentual para cada percentil según fórmula comparándola con la distribución obtenida de modo directo por la tabla de pesos (tabla 3). Puede apreciarse la homogeneidad de la distribución para la fórmula matemática aplicada. La diferencia del 1% observada para los percentiles 5 y 95, en nuestra opinión se debe a los casos extremos (patológicos) que escaparían a una distribución normal.

Tabla 3 En esta tabla se compara la distribución porcentual por percentiles de la muestra correspondiente a la validación. Obsérvese la gran similitud de resultados obtenidos con nuestro algoritmo y los esperados por percentiles. Los porcentajes descritos en «tabla de pesos» corresponden a los percentiles obtenidos mediante estudio descriptivo de una muestra de población (es una tabla «clásica» de pesos)
Validación		Algoritmo de peso		Tabla de pesos
percentiles	% acumulado	% en intervalo	% acumulado	% en intervalo
5	6,0	6,0	5,1	5,1
10	11,8	5,7	10,6	5,4
25	25,7	13,9	26,7	16,1
50	48,9	23,3	52,9	26,2
75	74,2	25,2	78,0	25,0
90	89,4	15,3	90,8	12,8
95	94,0	4,5	95,6	4,8
100	100,0	6,1	100,0	4,4

DISCUSION

Matemáticamente el método más fiable para estimar un percentil consiste en realizar un estudio estadístico descriptivo a partir de una gran muestra. De este modo se elaboran las tablas que, en realidad, transforman el peso en relación a la edad gestacional en una función discontinua (para las tablas un feto cumple semanas sin cumplir días intermedios); esto es así de manera artificial, ya que tanto la edad gestacional como el peso fetal son funciones continuas de forma natural.

Al partir de una muestra igualitaria de edades gestacionales, somos conscientes que están sobrerrepresentadas, con respecto a la población general, los casos extremos (pre y postérminos), y que dichos valores pueden influir significativamente en la estimación de la fórmula de peso y, en consecuencia, en la estimación de sus valores predictivos. Recomendamos, por tanto, cautela a la hora de aceptar un peso en dichos rangos, sobre todo considerando que muchos de dichos casos corresponden a gestaciones mal controladas y, en consecuencia, mal datadas.

Nosotros proponemos el uso de determinados algoritmos para la estimación de pesos fetales mediante regresión múltiple no lineal y todos los parámetros matemáticos más determinantes para la valoración diagnóstico-terapéutica de una gestación.

Esta fórmula, a nuestro entender, aporta las siguientes ventajas:

* Poder elaborar tablas de pesos con un número reducido de casos, ya que un determinado peso para una edad gestacional influirá en los datos adyacentes. Igualmente sucederá para la desviación estándar. Esto tiene particular interés para hospitales con un número reducido de partos, que no por ello deben desestimar los datos que emanan de su población «sometiéndolos» a resultados estadísticos de grandes hospitales. No obstante, ambos procedimientos no son incompatibles.

* Permite incluir en el informe de alta de cada puerpera el número de desviaciones estándar (Z) para su caso concreto (convertible a su correspondiente percentil mediante algoritmos matemáticos) con la simple inclusión de la fórmula en el programa informático y sin necesidad de introducir ningún nuevo campo.

* Elaborar un programa para ecografías que en función del peso estimado calcule, asimismo, el valor de Z. De este modo no sólo se obtiene un dato «bruto» de peso, sino también una medida de la dispersión.

* Permite elaborar estudios de diversa índole (por ejemplo: pesos fetales en distintas patologías) mediante procedimientos cuantitativos capaces de hallar la función numérica entre una determinada patología y su repercusión en el peso fetal, en vez de tener que recurrir a los clásicos resultados semicuantitativos (del tipo: un 20% de los casos se encontraron por debajo del percentil 10).

Sabemos que la estimación por fórmula del peso fetal es menos exacta estadísticamente que la obtenida mediante un estudio descriptivo de una población determinada, pero tampoco es más exacto aplicar resultados de grandes muestras a poblaciones pequeñas sometidas a otros factores distintos. Por otra parte, si bien es cierto que pueden existir incluso varios días de error en la datación de un embarazo, también sucede que con el sistema tradicional los siete días que corresponden a cada semana se asimilan a un mismo peso, por lo que cuando un feto entra en una nueva semana se produce de modo automático una reducción en su percentil correspondiente que oscila entre 5 y 15 puntos (¡siendo matemáticamente correcto!). Con nuestro sistema, aun existiendo dicho error de datación, la estimación progresiva del peso se mantendría uniforme, de tal manera que reflejaría más fielmente el percentil en que se encuentra un feto en un momento dado.

---

BIBLIOGRAFÍA

1 Rossavik IK, Deter RL. Mathematical modeling of fetal growth: I. Basic principles. J Clin Ultrasound 1984;12:529-33.