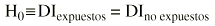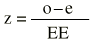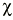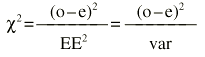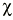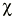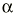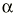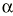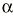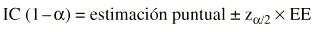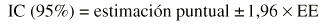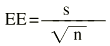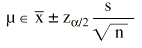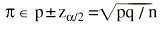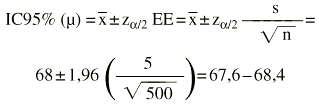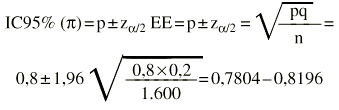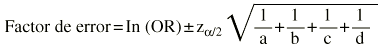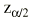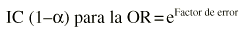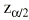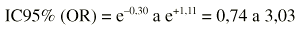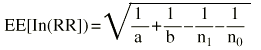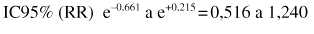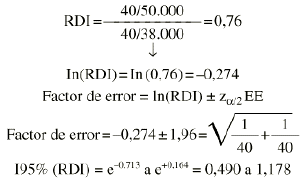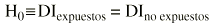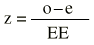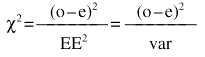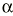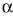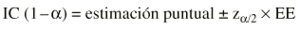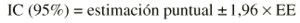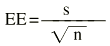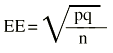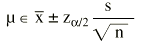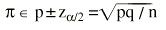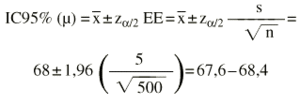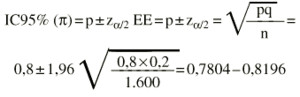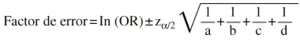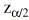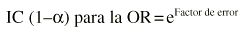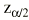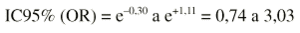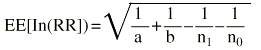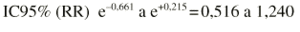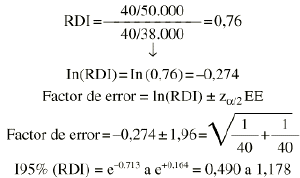TEMA DE ACTUALIZACIÓN
Conceptos básicos de bioestadística
Basic biostatistics concepts
MARTÍNEZ-GONZÁLEZ, M. A.
Unidad de Epidemiología y Salud Pública. Facultad de Medicina. Universidad de Navarra (Pamplona).
Correspondencia:
Prof. M. A. Martínez-González
Unidad de Epidemiología y Salud Pública.
Facultad de Medicina.
Universidad de Navarra.
Irunlarrea, s/n.
31080 Pamplona.
Recibido: Mayo de 1999.
Aceptado: Julio de 1999.
Se recogen en este capítulo algunos conceptos básicos comunes a los métodos estadísticos más aplicados en la investigación en Cirugía Ortopédica. Pueden ampliarse consultando revisiones más detalladas.1-3
Se han obviado algunos detalles referentes a demostraciones y exposiciones de carácter más matemático y se ha sacrificado en cierta manera el estricto rigor matemático de las explicaciones para centrarse fundamentalmente en la aplicación y la interpretación de los procedimientos básicos de la bioestadística. Es importante comenzar diferenciando los ámbitos de la bioestadística y de la epidemiología.
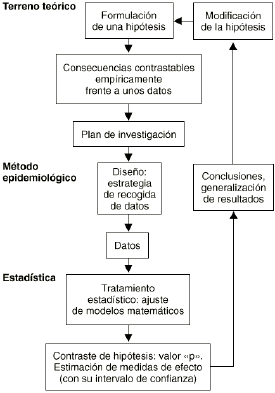
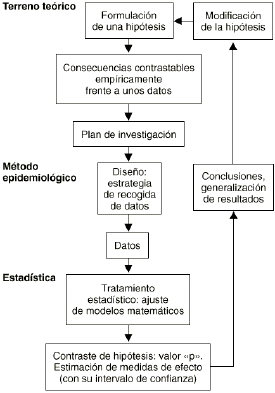
El ciclo seguido para desarrollar el abordaje epidemiológico de un determinado problema puede esquematizarse como se muestra en la figura 1. A diferencia del planteamiento meramente estadístico del contraste de hipótesis que acaba en un «valor p», el método epidemiológico va más allá, buscando la «medición del efecto». Un contraste de hipótesis nos diría simplemente si hay asociación entre una exposición y un efecto. Cuanto menor sea el valor «p» más probable será la existencia de una asociación. En cambio, el método epidemiológico no se conforma con buscar la significación estadística, sino que estima cuál es la magnitud de esta asociación a través del cálculo de parámetros como el riesgo relativo que nos dice cuántas veces es más probable el efecto en los expuestos que en los no expuestos.
Figura 1.
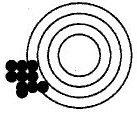
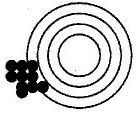
La epidemiología se concibe fundamentalmente como un ejercicio de medición: se trata de medir la ocurrencia de la enfermedad en una población y estimar determinados parámetros con el menor error posible, es decir, conseguir la máxima exactitud al medir. Los errores que se pueden cometer al medir son de dos tipos: sistemáticos o aleatorios. Por ejemplo, supongamos que un individuo (con poca puntería) está disparando con una escopeta a una diana. Como tiene mala puntería los distintos disparos que efectúa estarán muy separados unos de otros, rodeando toda la periferia de la diana sin acertar nunca en el centro. Evidentemente comete errores, pero son errores que pueden ir en cualquier dirección, son impredecibles. Supongamos que sólo el tirador ve la diana y nosotros sólo observamos dónde dan los disparos; si el tirador hiciera muchos disparos podríamos imaginar --a pesar de sus errores-- que el centro de la diana se encuentra en medio del espacio enmarcado por los disparos (Fig. 2).
Figura 2. Error aleatorio: falta de precisión.
Ahora supongamos otra situación. Un tirador (con buena puntería) usa una escopeta con un defecto de fábrica que sistemáticamente desvía los tiros hacia abajo y a la izquierda. Si el tirador efectuase muchos disparos sin darse cuenta del error que comete, los impactos estarán agrupados todos muy juntos entre sí, pero seguirán lejos del centro de la diana. Al observar los impactos sin ver la diana se obtendría la falsa impresión de que el centro de la diana está abajo y a la izquierda (en medio del espacio que circunscriben los disparos); es más, parecería que es más fácil saber dónde está el centro de la diana en esta segunda situación, pero se trataría de una equivocación. Esta situación es mucho más peligrosa porque además transmite la falsa imagen de que se está acertando al dejar todos los impactos unos muy cerca de otros (Fig. 3).
Figura 3. Error sistemático o sesgo: falta de validez.
A la primera situación se le llama error aleatorio (falta de precisión); en cambio a la segunda se le llama error sistemático o sesgo (falta de validez).
Las variaciones que ocurren por azar se llaman errores aleatorios y se producen por falta de precisión. A las variaciones introducidas por una mala medición o un mal diseño de un estudio epidemiológico y que conducen a un error que sistemáticamente se desvía del valor real se les llaman errores sistemáticos o sesgos y conducen a una falta de validez.
En estadística se trata fundamentalmente de estimar el error aleatorio, mientras que la epidemiología se ocupa preferentemente de prevenir y controlar los sesgos o errores sistemáticos, fundamentalmente a través de un correcto diseño de las investigaciones y de las estrategias de recogida de datos.
Los errores aleatorios:
a) Suponen un problema de falta de precisión. Cuanto mayor es el error aleatorio tanto menos precisa es la estimación (más se aleja del valor real).
b) El azar resulta en observaciones desviadas en cualquier dirección tanto por encima como por debajo del valor real, de modo que la media de los valores se acercará al valor real.
c) No son predecibles.
d) No pueden ser eliminados, pero sí reducidos mediante diseños más eficientes (que proporcionen mayor información sin necesitar observar a más sujetos) o aumentando el tamaño de la muestra estudiada.
e) El error aleatorio que persista a pesar de los intentos por reducirlo puede ser estimado estadísticamente.
En estadística se estima y se tiene en cuenta el error aleatorio al aplicar pruebas de contraste de hipótesis y en el cálculo de intervalos de confianza.
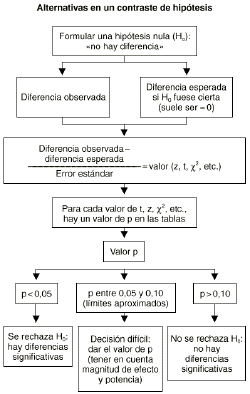
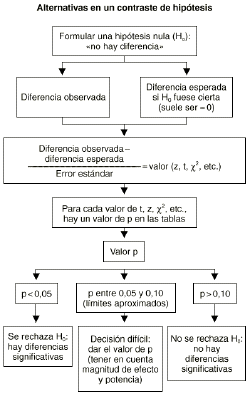
Contraste de hipótesis
El contraste o test de hipótesis podría equipararse a un juicio en el que al acusado se le concede en primer lugar la presunción de inocencia. A continuación, tras un proceso de recogida de pruebas por parte del fiscal, llega un momento en que se ve tan improbable que el acusado sea inocente que se le declara culpable.
La estadística cuando aplica un test parte también de una cierta «presunción de inocencia», ya que presume inicialmente que todas las diferencias que se observan se deben sólo al azar y no a ningún efecto. A esta presunción de inocencia que supone que el efecto no existe se le llama «hipótesis nula». Después viene una fase de recogida de datos y se calcula cuál es la probabilidad de observar esos datos (o unos más alejados todavía de la hipótesis nula) si realmente todo se pudiera explicar sólo por el azar.
Imaginemos un estudio en el que se desea evaluar si la exposición al tabaco incrementa el riesgo de fracturas por osteoporosis. La estrategia sería la siguiente:
Formular una hipótesis nula a priori
La hipótesis nula mantiene que las únicas diferencias que existen son debidas al azar: «la tasa de incidencia de fracturas osteoporóticas es la misma en expuestos y no expuestos al tabaco». Se suele representar gráficamente así:
H0 es la hipótesis nula y el símbolo «*» equivale a decir «mantiene que», «DI» es la densidad de incidencia o tasa.
Contrastar la hipótesis nula con los resultados obtenidos en la investigación concreta que se ha realizado
En el ejemplo anterior supongamos que se encontró que la tasa en expuestos era de 0,024 años1, mientras que en no expuestos era de 0,018 años1. Si la hipótesis nula fuese cierta, la razón entre las tasas (RT) sería exactamente igual a 1 (o la diferencia entre ellas sería exactamente cero), pero he aquí que la RT es de 1,33 (0,024/0,018 = 1,33). Nunca se va a encontrar una RT exactamente igual a 1 ni una diferencia exactamente igual a 0. ¿Por qué? Porque existe el error aleatorio. La pregunta siempre podría formularse así: ¿esta razón de 1,33 o esta diferencia de 0,006 años1 es debida simplemente al azar o, por el contrario, es debida a un «efecto» de la exposición al tabaco sobre el riesgo de fracturas osteoporóticas?
Calcular la probabilidad de hallar unos resultados como los hallados o más distantes aún de lo esperado bajo el supuesto de que la hipótesis nula fuese cierta
Si las diferencias que hemos hallado se hubiesen debido sólo al azar, ¿cómo de probable es hallar una razón de tasas de 1,33 o todavía mayor? Para saber responder a esta pregunta la estadística casi siempre recurre a realizar una división o cociente:
Aquí la diferencia observada (0,024 0,018 = 0,006) menos la esperada (0) es 0,006. ¿Cuál es el error aleatorio que hay que poner en el denominador? Esta pregunta es la que hace que los matemáticos trabajen (lo hacen muy bien) buscando cómo responderla en cada supuesto concreto. En general se puede decir que lo que hay que poner en el denominador es el error estándar. El buen trabajo de los matemáticos ha conducido a que estos cocientes sean en muchos casos directamente comparables con las puntuaciones «z» de la distribución normal. Para responder a la pregunta del contraste de hipótesis que compara la realidad con la hipótesis nula, sólo hay que buscar la probabilidad en ese modelo matemático que es la distribución normal tipificada. Esa probabilidad que se encuentra en la tabla de la distribución normal es la que proporciona la información sobre cuánto vale la cola de la distribución que queda a la derecha de un determinado valor z. Cada valor de z se corresponde con un valor p.
En general puede decirse que una prueba de hipótesis se suele reducir a lo siguiente:*
Donde «o» es lo observado, «e» es lo esperado y EE es el error estándar. Existe una distribución, la Ji cuadrado (
2), que supone una elevación de lo anterior al cuadrado:A veces al denominador de la Ji cuadrado se le llama varianza (var), pero realmente es el error estándar elevado al cuadrado, porque no es la varianza de la variable, sino de la
2.Decidir si se rechaza o no la hipótesis nula
Una vez que se ha encontrado el valor «p» correspondiente a cada z se interpreta que este valor «p» constituye la probabilidad de hallar nuestros datos bajo el supuesto de la hipótesis nula. Entonces se debe tomar una decisión. Si el valor de «p» es muy bajo habrá que pensar que sería muy raro encontrar tales datos si la hipótesis nula fuese cierta. Si el valor «p» no es muy bajo se pensará que en principio no hay argumentos en contra de la hipótesis nula y no se podrá rechazar.
Interpretación de los valores «p»
Habitualmente --aunque es algo arbitrario y no puede dársele una consideración estricta-- el límite para considerar que un valor de «p» es bajo se suele poner en p = 0,05. Cuando p < 0,05, se rechaza la hipótesis nula y se dice que el resultado es «estadísticamente significativo». En este caso habría que quedarse (provisionalmente) con la hipótesis alternativa (se suele representar como H1 o HA). En cambio cuando p >= 0,10, no se rechaza la hipótesis nula y se dice que no se alcanzó significación estadística.
¿Qué pasa cuando p está entre 0,05 y 0,10? Estamos en «tierra de nadie», se puede afirmar (siempre teniendo en cuenta la magnitud del efecto y la potencia del estudio) que «se aproxima a la significación estadística», de que hay una «tendencia» hacia el efecto. En general en esta circunstancia es mejor dar el valor concreto de p y no concluir ni por la significación estadística ni por la no significación. Que cada cual juzgue a la luz de un valor de p = 0,08. Por ejemplo, la interpretación más exacta de un valor de p = 0,08 sería la siguiente: si la hipótesis nula fuese cierta, habría una probabilidad del 8% de encontrar unos datos tan alejados como éstos o más de la hipótesis nula.
Las pruebas de significación estadística o de contraste de hipótesis intentan rechazar la hipótesis nula (H0) calculando la probabilidad de que los resultados observados (u otros más extremos aún) se produzcan sólo por azar. Se calcula la probabilidad de los datos condicional a que la hipótesis nula sea verdad. Esta probabilidad condicional es el grado de significación estadística (valor «p»). Se calcula aplicando diversas pruebas según el tipo de variables recogidas, como se verá más adelante, al final de este artículo. Tras aplicar la prueba estadística correspondiente, el resultado es rechazar o no rechazar H0. Si se rechaza H0 los resultados son estadísticamente significativos. Si no se rechaza H0 no hay diferencias estadísticamente significativas (Tabla 1).
Tabla 1. Decisiones posibles a partir de los valores «p» de significación estadística. | |
| p < 0,05 | p >= 0,10 |
| -- Se rechaza la hipótesis nula. | -- No se puede rechazar la hipótesis nula. |
| -- No parece que el azar lo explique todo. | -- No se puede descartar que el azar lo explique todo. |
| -- El «efecto» es mayor que el «error». | -- El «efecto» es similar al «error». |
| -- Hay diferencias estadísticamente significativas. | -- No hay diferencias estadísticamente significativas. |
| Los límites 0,05 y 0,10 son en cierto modo arbitrarios y aproximados. | |
Si en el ejemplo de la exposición al tabaco se hubiese obtenido un valor p = 0,01, la interpretación sería: si la exposición al tabaco no estuviese asociada al riesgo de fracturas osteoporóticas, la probabilidad de hallar una razón de tasas de 1,33 u otra todavía mayor sería del 1%. El valor p es, por tanto, la probabilidad de los datos (u otros más alejados de H0) si H0 fuese cierta. Es una probabilidad condicional. La condición es que H0 sea cierta.
La principal equivocación que se suele cometer en la investigación médica al interpretar los resultados de la estadística es creer que el valor p es la probabilidad de que H0 sea cierta. Pero la probabilidad de que H0 sea cierta no se puede calcular, ya que se necesita suponer que es cierta para poder calcular el valor p. Por tanto, nunca se puede decir si a la luz de nuestros resultados hemos hallado una p = 0,01 en el ejemplo anterior, que hay una probabilidad del 1% de que el tabaco no afecte al riesgo de fracturas osteoporóticas.
Los conceptos clave son:
-- Hipótesis nula (H0). Hipótesis que se pone a prueba tratando de rechazarla mediante una prueba estadística. Con frecuencia la hipótesis nula suele ser que no existe asociación y las diferencias observadas no se deben a un efecto de un factor que se estudia, sino simplemente al azar.
-- Hipótesis alternativa (H1). Hipótesis que se aceptará (provisionalmente) en caso de rechazar la hipótesis nula.
Interpretación correcta de un valor p: probabilidad de encontrar esa diferencia u otra todavía más alejada de la hipótesis nula, si la hipótesis nula fuese cierta.
Los valores p miden la fuerza de la evidencia estadística en muchos estudios científicos. Cuanto más bajo sea un valor p, mayor fuerza tienen las evidencias aportadas. Sin embargo, el valor «p» no mide la fuerza de la asociación entre dos variables o entre una supuesta causa y un efecto. Sólo indica la probabilidad de que un resultado al menos tan extremo como el observado se haya producido por azar. Los valores p son un modo de comunicar los resultados de una investigación, pero no definen por sí mismos la importancia práctica de unos resultados.
Es fácil cometer errores al interpretar los valores p. Por ejemplo, en el caso de la exposición al tabaco la interpretación equivocada sería decir que existe una probabilidad del 1% de que las tasas en expuestos y no expuestos sean iguales. No es así. Lo que existe es una probabilidad del 1% de encontrar una razón de tasas de 1,33 (diferencia = 0,006 años1) o mayor en una muestra, suponiendo que las tasas sean idénticas en la población de la que procede la muestra. La p se calcula en una muestra, pero se trata de extraer una conclusión acerca de una población. Es decir, si la muestra procediese de una población donde expuestos y no expuestos tienen la misma tasa habría una probabilidad del 1% de encontrar una diferencia de tasas de 0,006 años1 en una muestra de estas características. La característica de la muestra que más decisivamente influye en el cálculo de los valores p es el tamaño de la muestra. Con muestras de pequeño tamaño, a no ser que haya diferencias enormes entre grupos o entre mediciones, generalmente los valores p serán superiores a 0,10 y no se podrá rechazar la hipótesis nula. En cambio, con una muestra de gran tamaño (por ejemplo, n = 150.000) muchas de las diferencias por pequeñas que sean pueden resultar significativas y entonces hay que fijarse más en la magnitud de las diferencias encontradas que en los valores p. En general en epidemiología interesa más la magnitud de la asociación (valor del riesgo relativo, odds ratio o razón de tasas) que lo ínfimo que pueda parecer un valor p (Fig. 4).
Figura 4.
Errores en el contraste de hipótesis: riesgos alfa y beta
Error tipo I (riesgo
)¿Qué pasa si la hipótesis nula es en realidad cierta (la verdad es que no hay ningún efecto del factor bajo estudio), pero a pesar de todo se la rechaza? Si el criterio de rechazar la hipótesis nula es un valor p inferior al 5% (p <0,05) esto será lo que ocurrirá de hecho cinco de cada 100 veces en que la hipótesis nula sea cierta. Se llama a tales rechazos incorrectos de H0 «errores tipo I» o «errores alfa». Este error consistiría en decir que existen diferencias significativas cuando realmente no las hay. El riesgo alfa sería la probabilidad de cometer este error, es decir, la probabilidad de rechazar la hipótesis nula siendo ésta en realidad verdadera. Coincide con el valor p, lo que sucede es que se suele usar la terminología riesgo alfa cuando esta probabilidad se fija de antemano, estableciendo qué riesgo admitimos de cometer una equivocación; en cambio se calcula un valor p a posteriori a partir de los datos analizados. Una vez que se analizan los datos el valor p estima la probabilidad de cometer un error de tipo I si se decidiese rechazar la hipótesis nula. Volviendo a la analogía de un juicio donde la presunción de inocencia resulta análoga a la hipótesis nula, el error tipo I equivaldría a condenar a un inocente.
Error tipo II (riesgo ß)
El error de tipo II consiste en afirmar que no existen diferencias significativas cuando realmente las hay. El riesgo beta sería la probabilidad de cometer esta equivocación de no rechazar la hipótesis nula cuando ésta es en realidad falsa. Este error de no rechazar la hipótesis nula debiendo hacerlo se puede producir bien porque el efecto sea pequeño (diferencias reales pero de poca magnitud), bien porque el número de sujetos estudiados sea escaso (pequeño tamaño muestral) o por ambas cosas a la vez. Volviendo al símil del juicio, el error tipo II viene a equivaler a dejar suelto al culpable. La falta de diferencias significativas puede deberse a que en realidad no existan estas diferencias o a que se haya cometido un error tipo II. La probabilidad de cometer un error tipo II (no rechazar la hipótesis nula cuando se debería haber rechazado = decir que no hay diferencias cuando debería decirse que sí las hay) es el valor de ß (Tabla 2).
Tabla 2. Posibles resultados del contraste de hipótesis. | |||
| Verdad (realidad) | |||
| H0 | H1 | ||
| No se rechaza la hipótesis nula (el azar puede explicar todas las diferencias observadas en los datos) y es verdad. | No se rechaza la hipótesis nula (se dice que no hay diferencias significativas), pero nos equivocamos. | ||
| Decisión | |||
| H0 | H1 | ||
| Se rechaza la hipótesis nula (se dice que los resultados son estadísticamente significativos), pero nos equivocamos. | Se rechaza la hipótesis nula (se dice que los resultados son estadísticamente significativos) y es verdad. | ||
Potencia estadística
La potencia (1-ß) es la capacidad de una prueba para detectar una diferencia cuando ésta existe realmente. Cuanto menor sea el valor de ß, mayor es la potencia de una prueba para encontrar diferencias significativas.
La potencia es el complementario de ß: potencia = 1 ß (Tabla 3).
Tabla 3. Riesgos alfa y beta y potencia estadística. | ||
Verdad (realidad) | ||
| H0 | H1 | |
| H0 | 1- No error | ß Error tipo II |
| Decisión | ||
| H1 | Error tipo I | 1-ß No error (potencia) |
La aplicación práctica de los conceptos de riesgo ß y potencia es que al leer un trabajo de investigación que concluye diciendo que no se encontraron diferencias significativas se debe ser crítico y fijarse en cuál era la potencia de la prueba empleada para valorar tales diferencias; en concreto, un tamaño de muestra muy pequeño reduce la potencia y casi nunca se pueden encontrar diferencias significativas.
Considerando de nuevo la analogía con un juicio, normalmente se considera más grave condenar a un inocente (error tipo I) que no tener capacidad (potencia) para condenar al culpable por falta de pruebas (escaso tamaño muestral, error tipo II). Por este motivo los límites (alfa) del error tipo I suelen fijarse con más rigor (por ejemplo, riesgo alfa = 0,05) que los límites (beta) del error tipo II (por ejemplo, riesgo beta = 0,10 o bien 0,20).
Las pruebas de contraste de hipótesis más utilizadas aparecen en la tabla siguiente, agrupadas según el tipo de variables que se analicen. Se han escrito con mayúsculas aquellas pruebas llamadas «paramétricas» y con minúsculas las llamadas «no paramétricas».
Las pruebas paramétricas se llaman así porque se basan en parámetros (media, varianza, etc.) y requieren el cumplimiento de unas condiciones de aplicación más estrictas: normalidad, igualdad u homogeneidad de varianzas entre grupos, etc. Cuando no se cumplen estos supuestos (variables cuantitativas que no cumplen la hipótesis de normalidad, variables dependientes que siguen una escala ordinal...) se deben usar las pruebas no paramétricas (Tabla 4).
Tabla 4. | |||
| Variable independiente o predictora* | Variable dependiente o de respuesta** | Pruebas empleadas | Observaciones |
| Categórica | Categórica | Ji cuadrado. | Si muestra grande. |
| Prueba exacta de Fisher. | Si muestra pequeña. | ||
| Test de McNemar. | Medidas repetidas. | ||
| REGRESIÓN LOGÍSTICA. | Multivariante. | ||
| Categórica | Cuantitativa | «T» DE STUDENT. | Compara medias entre dos grupos. |
| ANÁLISIS DE VARIANZA. | Compara medias entre > dos grupos. | ||
| Mann-Whitney. | Dos grupos. No paramétrico. | ||
| Wilcoxon. | Dos grupos. Medidas repetidas. No paramétrico. | ||
| Kruskall-Wallis. | > dos grupos. No paramétrico. | ||
| Friedman. | > dos grupos. Medidas repetidas. No paramétrico. | ||
| Cuantitativa | Cuantitativa | REGRESIÓN. | Paramétrico. |
| CORRELACIÓN-PEARSON. | Paramétrico. | ||
| Correlación-Spearman. | No paramétrico. | ||
| REGRESIÓN MÚLTIPLE. | Multivante. | ||
| Categórica | Supervivencia | Kaplan-Meier. | Curvas supervivencia. |
| Long-Rank (Mantel-Haenzsel). | Comparación curvas de supervivencia. | ||
| REGRESIÓN DE COX. | Multivariante. | ||
| * Factor de riesgo, exposición, tratamiento, etc. ** Desenlace, efecto, enfermedad, etc. | |||
Por ejemplo, si se desea comparar el efecto sobre el dolor de dos analgésicos (A y B) cuya respuesta se ha medido en una escala ordinal (0: no mejora; 1: mejora algo; 2: mejora mucho, y 3: desaparece totalmente), se trata de comparar el efecto medio en dos grupos, no se debería utilizar una «t» de Student, sino la prueba de Mann-Whitney, que es no paramétrica.
Como puede deducirse de la tabla anterior, el tipo de datos que se analicen o la codificación que se haya usado en las diversas variables determinará cuál es el procedimiento estadístico más adecuado que se debe utilizar.
Pruebas a una cola y pruebas a dos colas
En el ejemplo de la exposición al tabaco, la hipótesis nula era que esta exposición no modificaba la tasa de incidencia de fracturas osteoporóticas. Pero, ¿cuál es la hipótesis alternativa? Si la única hipótesis alternativa que se plantea es que los expuestos presentan una tasa superior, estamos ante un alternativa unilateral. Pero la pregunta podría incluir también la otra alternativa: ¿no es posible que presenten una tasa inferior? En el caso de que interese considerar ambas posibilidades como hipótesis alternativa frente a la hipótesis nula de que no existen diferencias se estaría ante una hipótesis alternativa bilateral. En este último caso las pruebas estadísticas a utilizar se dice que son «de dos colas». En el primer caso serían sólo «de una cola». La consecuencia práctica es que al buscar en una tabla elegiremos el valor z, que se corresponde con las dos colas de la distribución normal (+z y z) si nuestra hipótesis alternativa H1 es bilateral, y sólo el valor p correspondiente a una cola si H1 es unilateral.
Cuando una prueba bilateral es significativa, también lo será una prueba unilateral. Las pruebas a dos colas siempre dan valores de p mayores (y por tanto con menor significación estadística) que las pruebas a una cola porque al formular dos preguntas se duplica la probabilidad de cometer un error tipo I.
A veces un investigador que no tenga muy claras las diferencias puede caer en la tentación de hacer trampas y al comprobar que no resulta significativa una prueba a dos colas buscar la significación estadística amparándose en que la prueba a una cola sí tiene un valor p < 0,05. Por esto la decisión de usar una prueba de una cola o una prueba a dos colas debe tomarse antes de iniciar el análisis de los datos y debe ser una decisión basada en el estado de conocimientos (en nuestro ejemplo, si ya hubiese muchos estudios que demuestran que los expuestos presentan tasas superiores, estaría justificado usar una prueba unilateral; en cambio si nos encontramos en los primeros pasos de una investigación y no hay muchos datos previos de otros estudios se deberían usar siempre pruebas a dos colas).
Cuando se mantiene una hipótesis basada en evidencias científicas o en la bibliografía se puede aceptar el uso de pruebas de una cola. Por ejemplo, si se está haciendo un ensayo clínico con un medicamento que en animales de laboratorio ha demostrado su efectividad, quizá estaría justificado utilizar una prueba de una cola. También se podría justificar el usar una prueba a una cola cuando la relevancia clínica o biológica de una alternativa en sentido distinto a la que estudiamos no representa ningún hallazgo de interés.
Pero esto son excepciones y, en general, es preferible usar siempre pruebas a dos colas, ya que si se usa una prueba a una cola siempre sería planteable argumentar que si está tan claro que el efecto va a ir en un sólo sentido entonces, ¿qué justificación tiene seguir investigando? Por otro lado, usar pruebas a una cola puede levantar la sospecha en el lector de que se recurre a ellas para encontrar tendenciosamente una significación estadística que no aparece cuando se usan las de dos colas.
Intervalos de confianza
La expresión «estadísticamente significativo» o «no significativo estadísticamente» se ha hecho muy común en las publicaciones médicas. Sin embargo, resulta muy pobre reducir a esta dicotomía las dos únicas conclusiones posibles de un estudio. El veredicto con apariencia de objetivo y concluyente que se quiere dar con estas frases resulta además falaz.
Un estudio que concluya que un efecto es «no estadísticamente significativo» puede haber cometido un error tipo II (especialmente si le falta potencia), y en realidad existiría el efecto a pesar de la rotundidad de la expresión «no significativo estadísticamente».
Por otro lado, un resultado con «altísima» significación estadística puede ser de «escasísima» magnitud y, por tanto, no tener ninguna relevancia. Por tanto, se debe evitar pronunciarse con ese énfasis cuando se presentan unos resultados. Existe un sesgo de publicación --especialmente preocupante en los metanálisis-- derivado de que es más fácil que se publique un estudio si sus resultados son estadísticamente significativos. Esta tendencia resulta peligrosa por la visión sesgada que a la larga se proporciona de las evidencias científicas disponibles. Incluso se debe evitar la tendencia a presentar un resultado como «positivo» si p < 0,05 y «negativo» si p > 0,05. También tiene un punto de incoherencia la expresión «no logró alcanzar significación estadística» como si esa fuese la meta a toda costa.
Un modo de superar estas limitaciones es presentar los resultados indicando un rango de valores del efecto que son creíbles a partir de los datos recogidos en el estudio. A este rango de valores se le llama intervalo de confianza.
El parámetro de interés debe encontrarse entre los valores extremos del intervalo de confianza. El nivel de fiabilidad del intervalo se llama «nivel de confianza». Normalmente se usan niveles de confianza del 95%. Más raramente se utilizan intervalos al 90 o al 99%. Un intervalo de confianza del 99% es más creíble que uno del 90%; sin embargo, el intervalo de confianza al 99% será más ancho (más distancia entre sus valores extremos) que el intervalo de confianza al 90%. El nivel de confianza es equivalente al complementario del riesgo
, es decir (1 ).A diferencia de una prueba de significación, un intervalo de confianza indica la mayor o menor precisión de los resultados (cuanto más estrecho sea el intervalo tanto más preciso es el resultado). Por ejemplo, si en un hipótetico estudio acerca de la eficacia de un nuevo tratamiento se curan 10 de 100 enfermos tratados y no existía ningún tratamiento alternativo eficaz, podemos decir que lo observado es 10/100 y lo esperado es 0/100. La comparación de ambas proporciones mediante una prueba estadística (prueba exacta de Fisher) otorgaría un valor de significación estadística p = 0,001. Con esto lo único que sabemos es que el tratamiento es mejor que nada. Pero para eso quizá no hubiese hecho falta hacer estadísticas. Más interesante es calcular el intervalo de confianza (IC), que en el ejemplo resulta ser: IC95%: 4,9-17,6. Ahora la conclusión del estudio ha mejorado. Diríamos que tenemos una confianza del 95% de que --para esa enfermedad hasta ahora incurable-- el porcentaje de curaciones que se logra con ese fármaco esté entre el 4,9 y el 17,6%.
La interpretación más precisa es que de los 100 intervalos que obtuviéramos con los datos de 100 estudios imaginarios distintos (100 muestras diferentes) que replicaran al que hemos hecho, 95 de ellos incluirían al verdadero valor del porcentaje de curaciones de la población de la que procede la muestra, y esperamos que éste (4,9-17,6) sea uno de los que lo incluye. O sea, en el 95% de las replicaciones del estudio el parámetro poblacional se encontrará dentro del intervalo. Este parámetro es el verdadero valor del porcentaje o proporción de curaciones en toda la población. No obstante, podríamos haber tenido mala fortuna y que nuestro intervalo sea precisamente uno de los cinco de cada 100 que no contienen al verdadero parámetro. Por eso tenemos una confianza del 95% de que lo incluirá.
El valor p (a dos colas) será inferior a 0,05 (es decir, «significativo») sólo cuando el intervalo de confianza al 95% no incluya el 0 en una diferencia o no incluya el 1 en una razón (o, de modo general, no incluya el valor correspondiente a la hipótesis nula). Si en el intervalo de confianza que hemos calculado no se contiene al valor correspondiente a la hipótesis nula (porcentaje: 0%) se puede afirmar que el efecto es significativo como pasa en el ejemplo. Pero si se redujera a esto la interpretación de un intervalo de confianza se estaría cayendo de nuevo en el mismo error reduccionista del pensamiento dicotómico que está en la base de la excesiva valoración de los valores p. La ventaja del intervalo de confianza sobre la significación estadística es que ahora se ha mejorado el modo de expresar el resultado porque se ha pasado de expresarlo en una escala dicotómica (significativo: sí/no) a expresarlo en una escala continua (4,9-17,6%).
Un intervalo de confianza ancho implica que el estudio tiene poca potencia estadística.
Un problema de la mayor parte de los métodos no paramétricos es que suelen utilizar una transformación de los datos originales en sus «rangos» (el lugar que ocupan al ordenarlos de menor a mayor). Son métodos que al no basarse en parámetros hacen muy difícil la obtención de intervalos de confianza. Están diseñados fundamentalmente para hacer pruebas de hipótesis. Por tanto, su aparente ventaja al no exigir supuestos previos se pierde porque muchas veces quedan reducidos a poder ofrecer sólo una respuesta de tipo sí/no.
En cambio cuando se usan métodos paramétricos las salidas que proporciona cualquier programa estadístico para ordenadores personales suelen reflejar el intervalo de confianza. Dependiendo del procedimiento estadístico y del programa informático utilizado proporcionarán el intervalo de confianza siempre o sólo cuando se le pide al ordenador explícitamente. Tener en cuenta el intervalo de confianza aporta dos aspectos interesantes al tratamiento estadístico de los datos: 1) establecer si existen diferencias significativas. Las hay cuando el valor p es inferior al 0,05, que suele ser el límite arbitrariamente fijado para dar un resultado como significativo, y 2) proporcionar el rango de valores creíbles para cada estimación puntual (intervalo de confianza).
Normalmente un intervalo de confianza suele estimarse así:
Donde z es el valor de la normal para dos colas y EE es el error estándar. Es importante diferenciar el error estándar (EE) de la desviación estándar (s). El error estándar (EE) proporciona información sobre la dispersión de un parámetro, mientras que la desviación estándar (s) proporciona información sobre la dispersión de los individuos de la muestra. Así, un intervalo de confianza al 95% sería:
El error estándar de una media viene definido por:
Y el error estándar de una proporción es:
Donde p es la proporción y q el complementario (q = 1 p) de la proporción.
Por tanto, el intervalo de confianza para una media vendría expresado por:
y para una proporción:
De todos modos es preciso tener en cuenta que para muestras pequeñas se debe usar la distribución «t» de Student y no la distribución normal para calcular el intervalo de confianza de una media. Veamos un ejemplo de cada caso.
Intervalo de confianza de una media
Se nos dice que la edad media de un grupo de 500 mujeres con osteoporosis que se van a someter a un ensayo clínico es de 68 años. La desviación estándar es de 5 años. ¿Cuál es el intervalo de confianza al 95%?:
Sería más exacto y riguroso utilizar la «t» de Student (con 499 grados de libertad), pero --dado que la muestra es grande-- las diferencias son inapreciables.
Intervalo de confianza de una proporción
La sensibilidad de una prueba es del 80%. Se ha calculado sobre 1.600 pacientes enfermos (1.280 verdaderos positivos y 320 falsos negativos).
El intervalo de confianza al 95% para la sensibilidad estaría entre 78,04 y 81,96%.
En el anexo se presentan las expresiones para el error estándar y el intervalo de confianza de otras medidas epidemiológicas de interés: riesgos relativos, odds ratios, etc.
Significación estadística y significación clínica
Es importante distinguir entre los conceptos de significación estadística y de significación o relevancia clínica. La significación estadística es la mayor o menor probabilidad de obtener un resultado como el observado en el estudio si todo se debiera sólo al azar. Por muy pequeña que sea una asociación o una diferencia, siempre que se disponga de tamaño muestral suficiente, dicha asociación o diferencia podrá ser estadísticamente significativa. La significación clínica es la importancia que en la práctica dicho resultado tiene para la mejora de la salud.
Supongamos que comparamos la eficacia de un nuevo fármaco B en relación al habitualmente utilizado (fármaco A), con vistas a su posible introducción en la práctica clínica. El fármaco A conduce a la curación del 85% de los pacientes tratados correctamente y el nuevo fármaco B al 87%, siendo la diferencia estadísticamente significativa (p < 0,001). ¿Significa ello que el nuevo fármaco B debe ser introducido en la clínica y que el fármaco A debe ser abandonado? Es ahora cuando hay que plantearse si la diferencia hallada tiene relevancia clínica, lo cual siempre implica un juicio subjetivo tras valorar los pros y contras de la introducción del nuevo fármaco B en la práctica.
* Se utiliza una prueba «z» cuando la distribución muestral del parámetro es normal. A veces es más útil una distribución llamada «t» de Student con cierto parecido a la normal, pero que introduce unas modificaciones para corregir el efecto de un pequeño tamaño de muestra. Entonces se dice que se usa una prueba «t», pero la forma de la prueba es similar a la indicada.
Bibliografía
Martínez-González, MA (Ed): Bioestadística. Aplicación e interpretación en ciencias de la salud. Pamplona. Newbook, 1997.
Martínez-González, MA, y Irala-Estévez, J (Eds): Métodos en salud pública. Pamplona. Newbook, 1999.
Atlman DG (Ed): Practical Statistical for Medical Research. Londres. Chapman and Hall, 1991.
Greenhalgh T: Statistics for the non-statistican. I: Different types of data need different statistical tests. BMJ, 364-366, 1997.
Greenhalgh T: Statistics for the non-statiscian: II: «Significant» relations and their pitfalls. BMJ, 422-425, 1997.
Anexo Error estándar e intervalos de confianza
Intervalo de confianza para una odds ratio (OR) mediante una aproximación a la distribución normal (método de Woolf)
Si la muestra es suficientemente grande los in-tervalos de confianza para una OR se pueden calcular por una aproximación a la distribución normal. Es un procedimiento sencillo, llamado método de Woolf,1 pero existen otros métodos como el de Miettinen2,3, que se conoce también como basado en el test (test-based). En el método de Woolf primero debe transformarse la OR logarítmicamente. El error estándar del logaritmo de la odds ratio vale la raíz cuadrada de la inversa de los efectivos (a, b, c y d) situados en cada una de las cuatro casillas de la tabla 2 * 2. Multiplicando este error estándar por el valor z de la distribución normal se obtiene una cantidad que se debe sumar y restar al ln(OR) para obtener sus límites. Llamamos factor de error a estas dos cantidades.
Donde ln(OR) es el logaritmo neperiano de la odds ratio,
es el valor de la distribución normal para el error alfa que se desee (z vale 1,96 cuando se desea un intervalo de confianza al 95%, ya que el error alfa sería del 5%) y «a», «b», «c» y «d» son los valores de cada una de las cuatro casillas en la tabla 2 x 2.Finalmente se eleva el número e a esas dos cantidades y ésos son los límites de confianza de la OR:
Ejemplo. Supongamos que se compara la efectividad de dos técnicas quirúrgicas distintas (A y B) y resulta una OR = 1,5. Si deseamos un intervalo de confianza al 95%,
valdrá 1,96 y los valores «a», «b», «c» y «d» serán los de la tabla 2 x 2:Una vez obtenidos los dos límites del factor de error basta con hallar la exponencial de ambos límites (elevar a esas cantidades el número e) para obtener el intervalo de confianza para la OR:
Intervalo de confianza para un riesgo relativo (RR) mediante una aproximación a la distribución normal (método de Woolf)
El procedimiento es el mismo que para la OR, pero el error estándar del ln(RR) es ligeramente diferente.
Ejemplo. Supongamos que se compara el riesgo de fracturas osteoporóticas entre las mujeres expuestas y no expuestas a terapia hormonal sustitutiva (THS):
Esto conduce a hallar los dos límites (0,661 y +0,215). A continuación se usan estos límites para revertir la transformación:
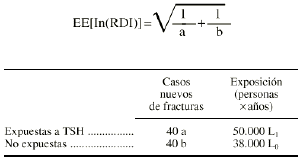
Intervalo de confianza para una razón de tasas o densidades de incidencia (RDI) mediante una aproximación a la distribución normal (método de Woolf)
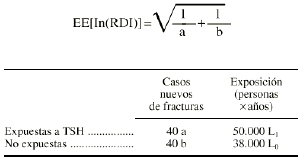
En este caso el error estándar viene dado por:
Supongamos el mismo ejemplo anterior, pero con personas-años en el denominador:
Bibliografía
1. Woolf, B: On estimating the relation between blood group and disease. Ann Hum Genet, 19: 251-253, 1955.
2. Miettinen, OS: Estimability and estimation in case-referent studies. Am J Epidemiol, 103: 226-235, 1976.
3. Gálvez-Vargas, R, y Delgado-Rodríguez, M: Estudios de casos y controles. En: Piédrola Gil, G; Del Rey Calero, J, y Domínguez Carmona, et al (Eds): Medicina preventiva y salud pública. Barcelona. Masson-Salvat, 1991, 116-126.