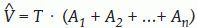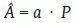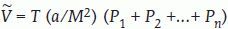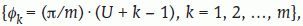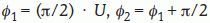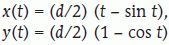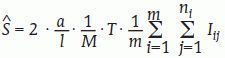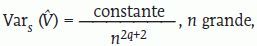La estereología como herramienta de cuantificación del volumen y la atrofia cortical en el cerebro del anciano con demencia

Introducción

La estereología es un conjunto de métodos que permiten la estimación insesgada y eficiente de cantidades geométricas definidas en estructuras arbitrarias. En particular, es una herramienta útil en la cuantificación de parámetros morfométricos cerebrales en estudios de neuroimagen. Por tanto, la estereología puede aportar una mayor objetividad en la evaluación complementaria y diagnóstica de ancianos con demencia, añadiendo datos cuantitativos a la evaluación clínica.

Objetivos y métodos

Nuestro objetivo es ilustrar la estimación del volumen cerebral y el área superficial de la corteza cerebral de un paciente anciano mediante procedimientos estereológicos cuantitativos asistidos por ordenador. Para estimar ambos parámetros se utilizó un diseño vertical con una serie de secciones paralelas de Cavalieri con orientación aleatoria y perpendiculares a un plano horizontal fijo. Las secciones se obtuvieron mediante resonancia magnética nuclear. Sobre ellas se superpusieron sondas sistemáticas (de puntos para el volumen y de cicloides para la superficie) mediante un software especial.

Resultados

Con objeto de explorar la variabilidad del error estadístico de las estimaciones, se utilizaron 5 o 10 secciones sistemáticas combinadas con dos densidades de puntos de sonda en la relación 1:4, de tal manera que el trabajo invertido varió en la relación 1:2:4:8. Los cuatro estimadores obtenidos variaron entre 986 y 1.120 cm³. Por otra parte, para el área de la superficie pial los estimadores variaron entre 1.947 y 2.096 cm², con cargas de trabajo variables en la relación 1:2:2.3:4.6.

Conclusiones

La estereología es una herramienta sencilla y eficiente, capaz de proporcionar estimaciones objetivas, no sesgadas por diseño, del volumen y la superficie cerebral pial con un coste modesto. Ello puede contribuir a facilitar la evaluación diagnóstica, evolutiva y pronóstica de pacientes ancianos con demencia.

Introduction

Stereology is a body of methods that allow unbiased and efficient estimation of geometric quantities defined in arbitrary physical structures. In particular, stereology is a valuable tool to assist neuroimaging in the estimation of morphometric parameters in the brain. Therefore, stereology may confer objectivity in the complementary and diagnostic evaluation of dementia by adding disease by adding quantitative data to clinical evaluation.

Objectives and methods

Our purpose was to illustrate estimation of brain volume and pial surface area by means of quantitative, computer-assisted stereological methods. Both parameters were estimated by means of a vertical design with a single series of parallel Cavalieri sections at a random orientation and perpendicular to a fixed horizontal plane. The sections were obtained by magnetic resonance imaging. Suitable test systems (of test points for volume, and of cycloids for surface area) were superimposed on these sections with the aid of special software. Results: to explore the statistical error of the volume estimator due to stereological sampling, 5 or 10 systematic sections were used in combination with two test point densities in a ratio of 1:4, so that the workload varied in the proportions 1:2:4:8. The four resulting estimators varied between 986 and 1120 cm³. The surface area estimators varied between 1947 and 2096 cm², with workloads varying in the proportions of 1:2:2.3:4.6.

Conclusions

Stereology is a simple and efficient tool to obtain objective brain volume and surface area estimators that are unbiased by design and accurate at a modest cost. Thus the corresponding methods can effectively assist in diagnostic and follow-up evaluation of elders with dementia.

INTRODUCCION

La demencia, además de ser una enfermedad con prevalencia creciente, tiene también importantes repercusiones sociales y familiares, así como sobre la calidad de vida y el grado de autonomía de los pacientes¹. Estas consecuencias nos apremian para la realización de un diagnóstico certero y lo más precoz posible, para intentar contrarrestar al máximo los devastadores efectos de esta patología^2,3. La mayor incidencia de estas enfermedades y el desarrollo de técnicas no invasivas de adquisición de imágenes (tomografía computarizada [TC], resonancia magnética [RM] y neuroimagen funcional) permiten ahondar en el estudio de la biología y el funcionamiento del sistema nervioso, y han propiciado un mayor interés por la neurobiología, con la posibilidad de estudiar y observar el cerebro humano en sujetos vivos, aspecto impensable hace unos años⁴. Entre todas las técnicas, la RM es la que más se está desarrollando a nivel general como herramienta de trabajo, y se emplea en la cuantificación y el estudio de las diversas estructuras cerebrales tanto en humanos, como en animales de experimentación^5,6.

La neuroimagen ha adquirido también un papel en la evaluación y el seguimiento de la demencia^7,8, y su realización rutinaria ha logrado mejorar la sensibilidad en el diagnóstico de esta afección^9-11. También se han desarrollado metodologías cuantitativas que permiten medir diversos parámetros morfométricos en distintas regiones del cerebro: corteza, sustancia blanca, ventrículos, etc. Los datos, habitualmente de tipo volumétrico, se pueden correlacionar con el envejecimiento, tipos de demencia y otras variables implicadas con la afección neurodegenerativa^12-14. Estas técnicas de morfometría cerebral abarcan desde procedimientos semicuantitativos hasta desarrollos informáticos amplios, semiautomatizados o totalmente automatizados, de cuantificación de las estructuras encefálicas. Aunque puede ser relativamente sencillo medir volúmenes de distintos compartimentos cerebrales mediante las técnicas comúnmente empleadas, el área de una superficie de forma arbitraria en tres dimensiones no es generalmente accesible mediante la metodología convencional. En el presente contexto la superficie pial de la corteza cerebral es de particular interés por dos aspectos. En primer lugar, su atrofia se podría correlacionar con los procesos neurodegenerativos. En segundo lugar, la superficie consta de numerosos pliegues y dos tercios de ella se encuentran localizados en el interior de los giros o surcos, por lo que su cuantificación mediante métodos directos o convencionales es compleja. Recientemente se ha desarrollado la morfometría basada en el voxel (MBV), que permite cuantificaciones volumétricas de sustancia blanca y corteza cerebral en múltiples afecciones^15,16. Sin embargo, no es frecuente encontrar estudios que cuantifiquen el área pial superficial de la corteza cerebral en la literatura científica^17-19. Este parámetro, área superficial de la corteza cerebral, puede ser un buen índice de atrofia cerebral a nivel cortical y, por tanto, un posible marcador diagnóstico o de estadio de la demencia en el paciente geriátrico.

A pesar de este auge de la morfometría cerebral, el empleo de técnicas más objetivas y sencillas basadas en la estereología, y que hacen a la neurobiología más objetiva²⁰, está poco desarrollado en dicho campo. Los sistemas de cuantificación del cerebro son múltiples, pero debido a la irregularidad en la forma, así como a la presencia de numerosos surcos y circunvoluciones, las estimaciones resultantes suelen presentar sesgos. La estereología es una herramienta matemática, que mediante procedimientos insesgados y objetivos, es muy adecuada para la evaluación de parámetros geométricos de estructuras de forma arbitraria. Entre los parámetros que puede estimar (en cualquier dimensión) figuran: número de objetos o partículas, longitud de estructuras curvilíneas, área (de una figura plana o de una superficie), volumen, etc.^21-23. Para ello se emplean sondas geométricas de propiedades conocidas, como por ejemplo una serie de planos paralelos a una distancia constante, una rejilla periódica de puntos, líneas o ventanas, etc. En la llamada estereología por diseño, que es la que nos ocupa, el objeto se supone fijo, mientras que la sonda es sometida a una traslación uniforme aleatoria (y, si procede, también a una rotación uniforme aleatoria, es decir isótropa) cortando al objeto. La muestra es la intersección observada entre el objeto y la sonda. Mediante argumentos matemáticos basados en la probabilidad geométrica se obtienen ecuaciones exactas que expresan el parámetro de interés del objeto (p. ej., su volumen o el área de su superficie) en función de valores medios de cantidades fácilmente medibles en la muestra^24,25. Es importante recalcar que la estereología no puede garantizar la ausencia de sesgos causados por la manipulación del material, microtomos, defectos de resolución de microscopios o imágenes radiológicas, o técnicas de rastreo, etc. Sin embargo, sí garantiza, al menos, la ausencia de sesgo en lo que concierne al diseño de muestreo de imágenes, cuya inadecuación suele ser la fuente de sesgo más importante. Estos y otros aspectos importantes en la estereología se han recogido en los últimos años en diversas publicaciones^26-29_.

Los datos procedentes de un diseño de estereología son casi siempre números enteros porque reflejan conteos de sucesos fácilmente observables, como son las intersecciones del objeto con puntos y líneas de sonda repartidos sistemática y uniformemente al azar en el espacio. Todo ello confiere una robustez y eficiencia muy altas a los correspondientes estimadores, a pesar de utilizarse intensidades de muestreo muy bajas. Existen además fórmulas para predecir la variancia del error de muestreo con distintos diseños sistemáticos a partir de la muestra^27,30. La deducción matemática de esas fórmulas no es trivial porque los datos suelen estar fuertemente correlacionados, pero su uso es simple. Las predicciones no son insesgadas en general, pero son muy útiles a la hora de planificar los tamaños muestrales en las distintas fases del diseño. Las estructuras biológicas siguen siendo uno de los principales campos de desarrollo e investigación en estereología^20,29.

El objetivo central del presente artículo es describir un método para la estimación del área pial superficial de la corteza cerebral mediante estereología. Como complemento, y aunque su uso está más extendido, ilustramos también la estimación del volumen cerebral por el método de Cavalieri, el cual se puede obtener de forma simultánea. No entra dentro de los objetivos del presente trabajo la realización de un estudio normativo de morfometría cerebral en ancianos sanos y con demencia. Este aspecto será desarrollado en un futuro próximo.

MATERIAL Y MÉTODOS

Material y equipos

Con objeto de implementar e ilustrar los métodos descritos en este artículo, se ha contado con la colaboración voluntaria de un anciano sano (72 años, 168 cm y 79 kg). Para obtener las secciones virtuales en la forma descrita más abajo se utilizó un resonador General Electric modelo Sigma Horizon. La secuencia es 3DT1 llamada SPGR 3D. Los parámetros de adquisición son: TE: min; Flip angle: 15; Freq: 256; Phase: 192; 1 Nex; FOV: 25 cm. El tiempo de adquisición es de, aproximadamente, 7 min.

Las imágenes de formato DICOM se transformaron mediante la aplicación informática MRIcro³¹. El análisis estereológico de las secciones cerebrales se facilitó notablemente mediante el software especial EasyMeasure (del Magnetic Resonance and Image Analysis Research Centre, Universidad de Liverpool, Reino Unido³²), que genera en la pantalla de un ordenador las sondas de puntos y curvas sistemáticos necesarios para el análisis. La adquisición de datos es, sin embargo, manual, de manera que se trata de un método semiautomático de análisis de imagen.

Estimación del volumen cerebral por el método de Cavalieri

Comenzamos considerando el problema general de estimar el volumen V de un objeto tridimensional de forma arbitraria, fijo y acotado. Imaginemos un eje (que llamaremos el «eje de muestreo») de dirección arbitraria. Sobre este eje generamos una malla sistemática de puntos a una distancia dada T, de tal manera que uno de los puntos es aleatorio uniforme en el intervalo (0, T). A continuación generamos un plano de sección perpendicular al eje de muestreo por cada uno de los puntos de la malla. El resultado es una sonda sistemática de planos paralelos (fig. 1b y c). Si cortamos el objeto con esa sonda, obtenemos una muestra sistemática de áreas de sección {A₁, A₂, …, A_n}. Es fácil demostrar que:

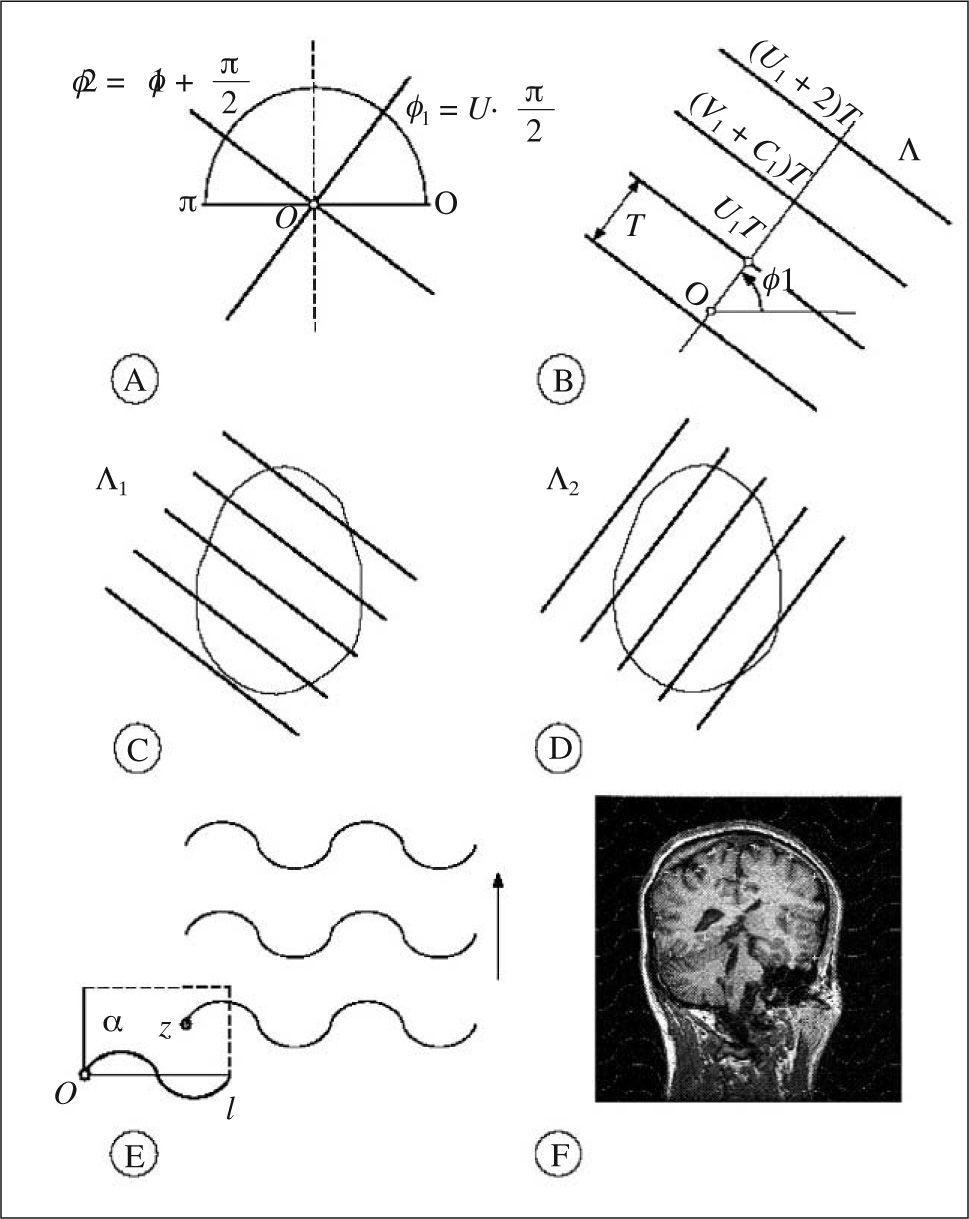
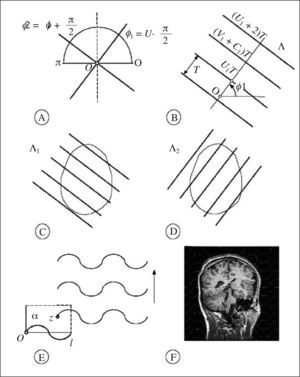
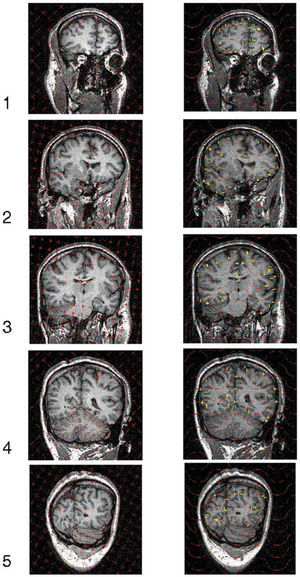
es un estimador insesgado de V. Nótese que el estimador depende de un solo número aleatorio en el intervalo (0, T). En la práctica, basta con comenzar a generar los planos de sección desde fuera del objeto e independientemente de la posición de éste. «Insesgado» quiere decir que para cualquier valor de T la media de todas las realizaciones de Vˆ obtenidas mediante extracciones repetidas de un número aleatorio, es precisamente V. Además Vˆ es «consistente», es decir que converge a V cuando T tiende a cero. El número n de secciones es, en general, aleatorio, con dos valores posibles. El estimador (1) se conoce en estereología como el «estimador de Cavalieri», en honor del matemático italiano Bonaventura Cavalieri (1598-1647), discípulo de Galileo, cuyo celebrado teorema relaciona directamente volumen y área de sección²⁶.

Figura 1.

Ilustración de un diseño vertical con dos direcciones sistemáticas. A: dos direcciones sistemáticas de período π/2. La cantidad U es un número aleatorio entre 0 y 1. B: generación de una serie de planos verticales de Cavalieri perpendiculares al eje de muestreo de dirección φ₁. El plano del papel es el plano horizontal y las rectas paralelas son las trazas determinadas por los correspondientes planos verticales con el plano horizontal. U₁ es un número aleatorio entre 0 y 1, de tal manera que U₁T es un número aleatorio entre 0 y T. C y D: diagramas de las proyecciones de dos series sistemáticas de planos de sección verticales de Cavalieri cortando a un mismo cerebro con objeto de estimar el área de cualquier superficie definida en el mismo. El plano horizontal, que coincide con el plano del papel, es el plano axial. E: porción de una sonda de cicloides con longitud por área l/a, conocida. La flecha señala la dirección vertical. El punto z es uniforme y aleatorio en el interior del rectángulo fundamental de la sonda. F: sección virtual vertical de un cerebro humano obtenida mediante resonancia magnética. La sección pertenece a una serie vertical de Cavalieri. La sonda de cicloides es uniforme y aleatoria como se describe en (E), generada con el software EasyMeasure (Universidad de Liverpool). Las intersecciones con la superficie pial vienen señaladas con cruces. El área de la superficie tridimensional se estima mediante la ecuación (7).

Por otra parte, cada área de sección puede medirse por un procedimiento automático si el objeto se presta a una segmentación sistemática sencilla. Éste no suele ser el caso en estructuras biológicas, y el cerebro no es la excepción. Ello no constituye un serio problema, porque esas áreas se pueden estimar de una manera fácil y muy eficiente mediante el método de conteo de puntos. Por ejemplo, para estimar el área A de una figura plana cualquiera generamos una malla sistemática de puntos en el plano, la superponemos sobre la figura uniformemente al azar, y contamos el número P de puntos que cortan a la figura. Entonces:

es un estimador insesgado de A, donde a es el área que corresponde a un punto de la malla. Por ejemplo, para una malla o rejilla cuadrada de lado d, se obtiene a = d². Para cada orientación de la rejilla, el estimador Â, depende de dos números aleatorios e independientes en el intervalo (0, d). En la práctica basta con superponer la rejilla «al azar» sobre la imagen^27,29.

Si sustituimos en el segundo miembro de la ecuación (1) cada área por su estimador insesgado (2), obtenemos el nuevo estimador:

donde M es el aumento lineal de las secciones analizadas, de manera que a/M² representa el área por punto de la rejilla corregida a la escala del objeto. El estimador de Cavalieri (3) es también insesgado, al menos en lo que respecta al diseño de muestreo^33,34.

Estimación del área superficial de la corteza cerebral mediante secciones verticales

El problema general es estimar el área S de una superficie fija y acotada de forma arbitraria. La representación más adecuada para construir un estimador insesgado de S es la que relaciona S con el número I de intersecciones entre la superficie y una recta isótropa y uniforme («IUR») cortando a la superficie^27,29. La integral de I para todas las posiciones de la recta IUR cortando a la superficie es igual a πS. La consecuencia básica es que un estimador insesgado de S es proporcional a I.

El procedimiento clásico para generar rectas IUR consiste en cortar primero el objeto mediante una sección plana IUR, y luego generar una recta IUR en este plano. En biología el uso de secciones planas IUR es a menudo incómodo. Mucho más cómodo es recurrir al diseño vertical. Fijemos un plano arbitrario al que llamaremos «plano horizontal». Por ejemplo, el plano de una mesa sobre la que depositamos un cerebro de la manera habitual, es decir, un plano perpendicular al eje axial, se puede adoptar como plano horizontal. Un plano vertical es perpendicular al plano horizontal, y la recta de intersección entre ambos es, a su vez, isótropa y uniforme en el plano horizontal. Es decir, a un plano vertical se le permite girar y desplazarse con densidades de probabilidad uniformes e independientes, permaneciendo siempre perpendicular al plano horizontal^35,36. La idea central es que cualquier recta del espacio se puede incluir en un plano vertical y, por tanto, es posible generar rectas IUR en planos verticales; no es necesario utilizar planos orientados al azar en el espacio, lo cual supone una gran ventaja en la práctica. Consideremos una recta en un plano vertical. Para que esta recta sea efectivamente IUR en el espacio es necesario observar un detalle técnico: el ángulo θ que forma con el eje vertical no es uniforme; su densidad de probabilidad es 12sinθ,(φ≤φ<π). Por ejemplo, si elegimos un número aleatorio U en el intervalo (0,1), entonces θ = arccos(1 –2U) tiene la densidad de probabilidad correcta. Ahora bien, en lugar de generar rectas uniformes ponderadas por el seno, se puede recurrir a una curva que tiene la propiedad deseada: el elemento de longitud de esta curva en un punto donde la tangente forma un ángulo θ con el eje vertical, es proporcional a sinθ, es decir: ds(θ) = sinθ dθ. Esta curva es la clásica cicloide con su eje menor paralelo al eje vertical (fig. 2).

Figura 2.

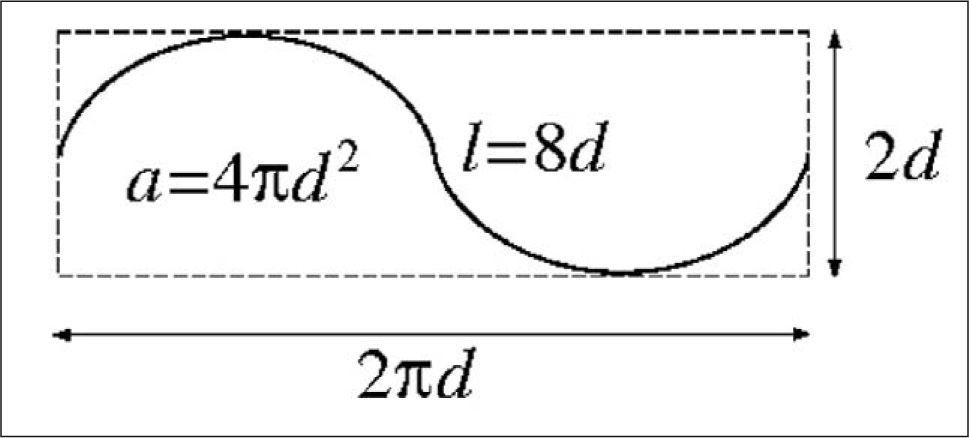
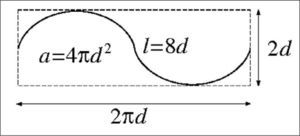
Sonda de cicloides. La sonda de cicloides utilizada en este estudio es una partición del plano formada por las translaciones periódicas de la figura o «baldosa» fundamental dada. La constante relevante para estimar el área de una superficie mediante secciones verticales (figs. 3 y 4) utilizando la ecuación (7), es a/l = πd/2 en este caso.

Las consideraciones precedentes conducen a un diseño vertical cómodo en la práctica, especialmente si la superficie de interés se puede observar en secciones no invasivas, como es el caso en el presente contexto. Con referencia a la figura 1, el diseño consta de los siguientes pasos.

• 1.

  Fijamos un eje de referencia Ox como origen de ángulos en el plano horizontal. Si deseamos rastrear en m direcciones sistemáticas, entonces el período es π/m. Trazamos m ejes formando ángulos φ₁, φ₂,..., φ_mcon Ox y dados por:

  
  donde U es un número aleatorio en el intervalo (0,1). Por ejemplo, si deseamos rastrear en dos direcciones perpendiculares, éstas serán:
  

• 2.

  Perpendicular a cada dirección sistemática φ_i construimos una serie Λ_i de planos de Cavalieri a una distancia fija T, tal que una sección dista U_nT unidades de longitud de O, donde U_i es un número aleatorio en el intervalo (0,1). Los números aleatorios {U₁, U₂,…,U_m} son independientes. La serie Λ_i producirá un total de n_i secciones no vacías en la superficie de interés.

• 3.

  En cada plano de cada serie vertical Λ_i superponemos una sonda sistemática de cicloides uniformemente al azar, pero manteniendo el eje vertical de las cicloides siempre paralelo al eje vertical. Esta operación necesita dos números aleatorios e independientes. Para los planos sucesivos se pueden generar nuevas translaciones independientes de la sonda. Sin embargo, si el procedimiento viene asistido por ordenador, para los planos sucesivos se puede mantener la sonda en su posición aleatoria inicial. Para generar cicloides con software gráfico es útil conocer sus ecuaciones paramétricas. Éstas son:

  

  La cota máxima y(π) = d corresponde al eje menor de la cicloide. La longitud de un arco completo descrito entre t = 0 y t = 2π es 4d, es decir 4 veces el eje menor (fig. 2). Con esto es fácil determinar la razón l/a de la longitud de cicloide por área de sonda, que es el único parámetro relevante de la sonda. El número de cicloides, su disposición en el plano y su tamaño no intervienen en el estimador (véase la ecuación [7]).

• 4.

  Llamemos I_ij al número de intersecciones entre la superficie de interés y la sonda de cicloides en la j-ésima sección vertical, (j = 1, 2, …, n_i) de la i-ésima serie vertical de Cavalieri Λ_i, (i = 1, 2, …, m). Se demuestra que un estimador insesgado de S es:

  
  donde M es el aumento lineal al que se analizan las secciones^27,35.

RESULTADOS

Resultados de la estimación del volumen cerebral

Para estimar el volumen cerebral (excluyendo cerebelo ventrículos) y el área total de la superficie pial del anciano citado en la sección «Material y equipos» se adoptó el plano normal al eje axial como plano horizontal. En la práctica, para estimar el área de una superficie es recomendable generar al menos 2 series de planos de sección de tipo Cavalieri verticales y mutuamente perpendiculares (fig. 1c y d). Para el presente ejemplo generamos solamente una serie, es decir tomamos m = 1 en la ecuación (4). El ángulo aleatorio elegido fue φ = 72°. Con este ángulo se obtuvieron cortes virtuales como se indica en la figura 1b, a una distancia inicial de 1,5 mm. De estas secciones se eligió una de cada 10, con un comienzo aleatorio entre 1 y 10. De este modo se obtuvo una muestra de 10 secciones verticales paralelas a una distancia de 1,5 cm. Las secciones sirven para estimar la superficie y el volumen (para el cual bastan secciones de Cavalieri en una dirección cualquiera). Con objeto de explorar la precisión se analizaron también las 2 submuestras formadas por las 5 secciones pares e impares respectivamente (fig. 3).

Figura 3.

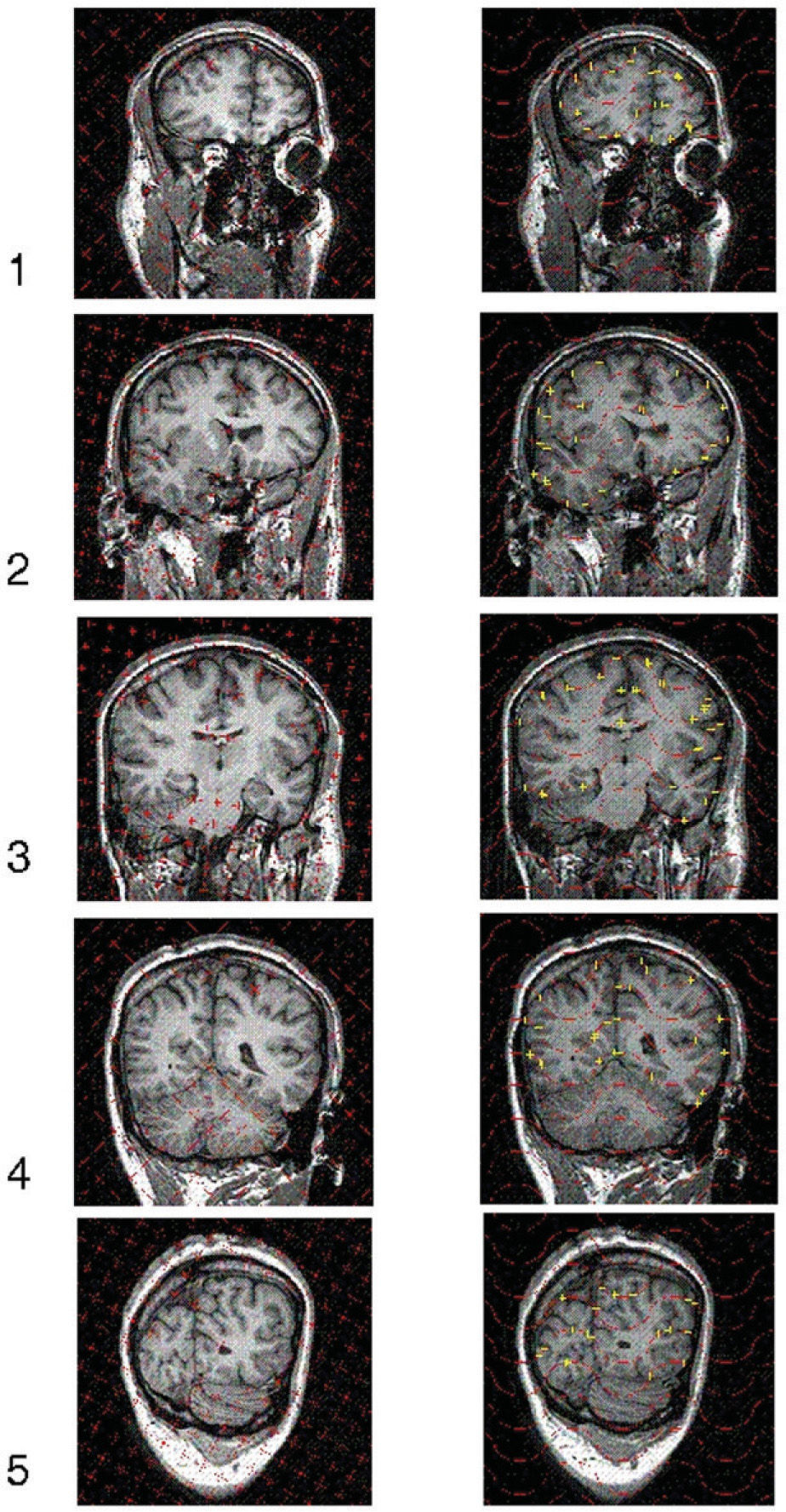
Ilustración de la toma de datos para estimar volúmenes y superficies reales mediante 5 cortes verticales con una dirección aleatoria. Muestra de 5 secciones verticales virtuales, obtenidas mediante resonancia magnética, a un ángulo φ = 72° (fig. 1) y a distancia constante T = 3 cm. La base de cada rectángulo (es decir, el field of view, FOV) mide 25 cm en todos los casos. Columna izquierda: plantilla de puntos superpuesta al azar en cada sección para estimar el volumen cerebral; los puntos que cortan al cerebro son identificados y marcados con el ratón por el usuario y automáticamente contados y eliminados mediante el software EasyMeasure (Universidad de Liverpool). Luego se aplica la ecuación (3). Columna derecha: plantilla de cicloides (fig. 2) superpuesta al azar con el eje menor de las cicloides paralelo a la dirección vertical (fig. 1) para estimar la superficie pial. Cada intersección con la superficie pial es identificada y marcada con el ratón por el usuario y automáticamente contada y sustituida por una cruz. Luego se aplica la ecuación (7). Para más detalle véase la figura 4.

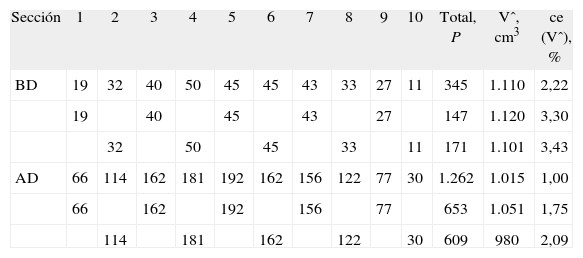
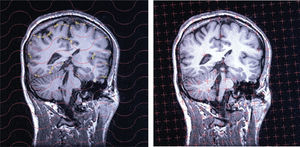
La imagen de cada sección quedó incluida en una ventana cuadrada de 25 cm de lado (es decir, el field of view, [FOV], era de 25 cm). Para estimar el volumen, sobre cada ventana se superpuso una sonda de puntos uniformemente al azar (véase la sección «Estimación del volumen») mediante el software EasyMeasure ya citado (fig. 3, primera columna, y fig. 4, panel izquierdo). El usuario marca con el ratón cada punto que corta al cerebro, y ese punto es contado y borrado de la pantalla automáticamente. Para explorar la eficiencia, para cada muestra de 5 y 10 secciones se utilizaron 2 sondas de rejilla cuadrada de 1,46 y 0,73 cm de lado, respectivamente. De este modo se recogieron los datos recogidos en la tabla 1. La tabla recoge también los correspondientes resultados obtenidos mediante la ecuación (3).

Figura 4.

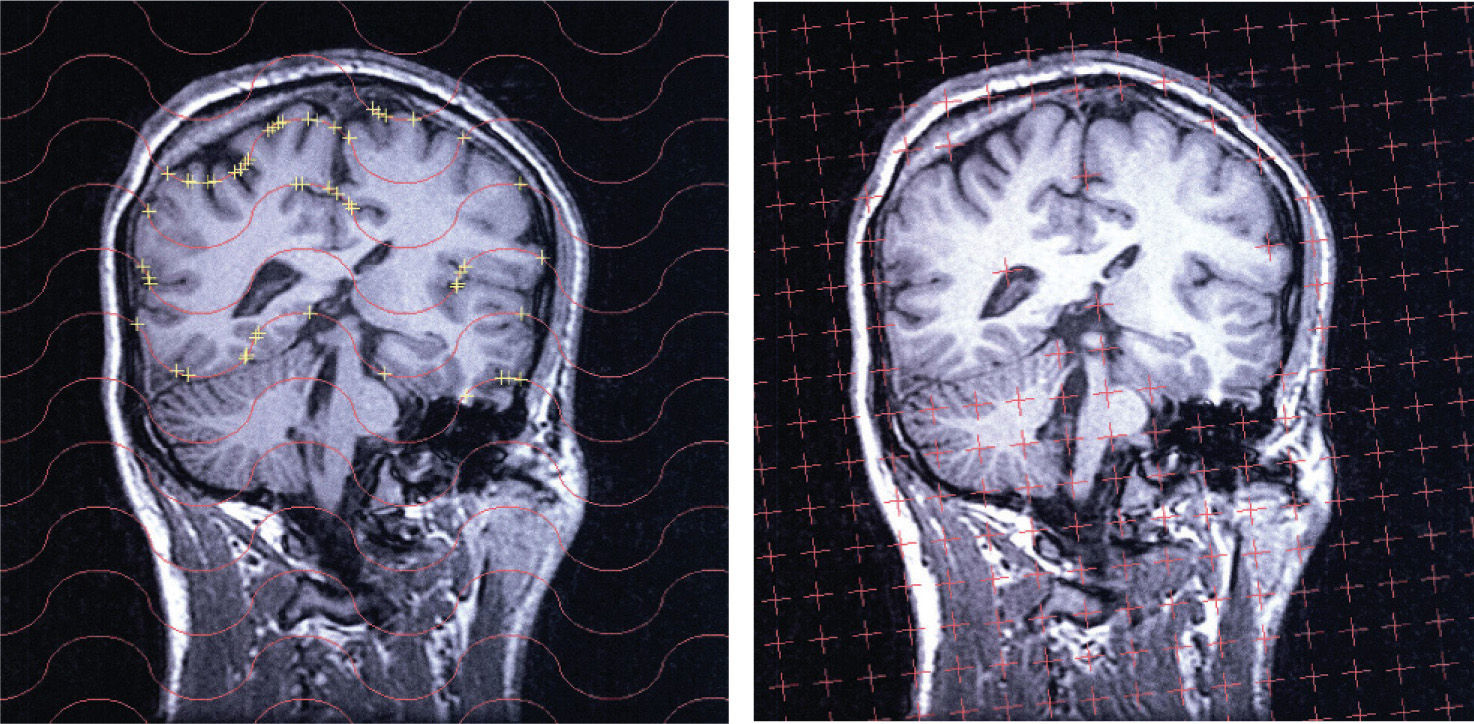
Detalles del análisis de una sección. Detalle de una sección vertical con mayor detalle que en la figura 3, con objeto de mostrar los detalles relativos a la toma de datos. Izquierda: los puntos de corte con el cerebro (para estimar su volumen) han sido contados y eliminados automáticamente. Derecha: intersecciones (cruces amarillas) entre las cicloides de la sonda y la superficie pial para estimar su área. FOV = 25 cm.

Tabla 1.

Datos de los volúmenes cerebrales

Sección	1	2	3	4	5	6	7	8	9	10	Total, P	Vˆ, cm^3	ce (Vˆ), %
BD	19	32	40	50	45	45	43	33	27	11	345	1.110	2,22
	19		40		45		43		27		147	1.120	3,30
		32		50		45		33		11	171	1.101	3,43
AD	66	114	162	181	192	162	156	122	77	30	1.262	1.015	1,00
	66		162		192		156		77		653	1.051	1,75
		114		181		162		122		30	609	980	2,09

Número de puntos de sonda (P) contados en cada sección (fig. 3, columna izquierda) y estimadores (Vˆ) del volumen cerebral (ecuación [3]) con sus correspondientes coeficientes de error en % (= 100 × error típico del estimador/valor del estimador), obtenidos como se indica en el texto («Precisión de los estimadores»). Para explorar la precisión empírica se analizan la muestra completa de 10 secciones y cada una de las dos muestras formadas por las secciones pares e impares.

AD: alta densidad de puntos de sonda (área/punto = 0,5364 cm²). BD: baja densidad de puntos de sonda (área/punto = 2,1458 cm²). Ambas densidades corregidas por el aumento final.

Resultados de la estimación del área de la superficie pial cerebral

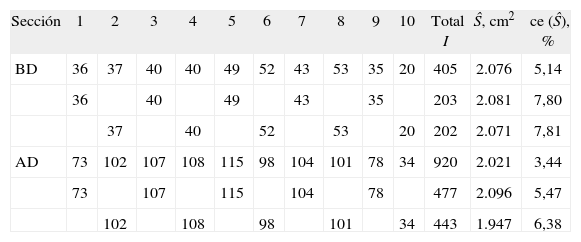
Para estimar el área de la superficie pial la sonda adecuada consta de cicloides, curvas especiales (Ec. [6]), cuyo uso se ya ha justificado (véanse la figura 3, segunda columna, y la figura 4, panel derecho). Para cada muestra de 5 y 10 secciones se utilizaron 2 sondas con cicloides cuyo eje menor d era de 1,088 y 0,466 cm, respectivamente (fig. 2). Los correspondientes datos y resultados (obtenidos mediante la ecuación [7]) se recogen en la tabla 2.

Tabla 2.

Datos de la superficie cerebral

Sección	1	2	3	4	5	6	7	8	9	10	Total I	Ŝ, cm^2	ce (Ŝ), %
BD	36	37	40	40	49	52	43	53	35	20	405	2.076	5,14
	36		40		49		43		35		203	2.081	7,80
		37		40		52		53		20	202	2.071	7,81
AD	73	102	107	108	115	98	104	101	78	34	920	2.021	3,44
	73		107		115		104		78		477	2.096	5,47
		102		108		98		101		34	443	1.947	6,38

Número de puntos de intersección (I) contados en cada sección (fig. 3, columna derecha) y estimadores (Ŝ) del área de la superficie pial (ecuación [7]) con sus correspondientes coeficientes de error en porcentaje, obtenidos como se indica en el texto («Precisión de los estimadores»). Para explorar la precisión empírica se analizan la muestra completa de 10 secciones y cada una de las dos muestras formadas por las secciones pares e impares.

AD: alta densidad de cicloides (área/longitud = 0,7325 cm). BD: baja densidad de cicloides (área/longitud = 1,7090 cm). Ambas densidades corregidas por el aumento final.

Precisión de los estimadores

La precisión requerida para cada estimador es una consecuencia de los objetivos fijados en cada experimento o proyecto. Alguna de las variables que intervienen son: a) la diferencia que se desea detectar, bien sea entre las medias de dos poblaciones —p. ej., controles y tratados— o bien entre un individuo determinado y la media de una población de referencia; b) la variación biológica del parámetro de interés en la población, y c) la variación (estereológica en este caso) debida al muestreo. Los tamaños muestrales en las distintas etapas de muestreo (individuos, secciones, puntos o curvas de sonda, etc.) dependen de esas variables. Los correspondientes criterios estadísticos a utilizar —en un contexto estereológico— están descritos recientemente³⁷.

El único aspecto que distingue un diseño estereológico como el descrito en este artículo de uno ordinario radica en la predicción de la variación debida al muestreo³⁸. En efecto, en estereología se usa el muestreo sistemático, casi siempre mucho más eficiente que el muestreo aleatorio simple pero en el cual no se cumplen las relaciones matemáticas habituales para este último²⁷. Desafortunadamente, las predicciones de la variancia de un estimador obtenido por muestreo sistemático no son insesgadas sino meras aproximaciones. Por otra parte, la teoría conducente a las aproximaciones es bastante compleja³⁹. Las predicciones correspondientes al diseño de Cavalieri son las mejor conocidas, y las fórmulas de predicción más recientes pueden verse en bibliografía reciente³⁰; el volumen correspondiente del Journal of Microscopy 2006 (222 Part 3) está dedicado enteramente a problemas análogos, y en él puede consultarse casi toda la bibliografía relevante.

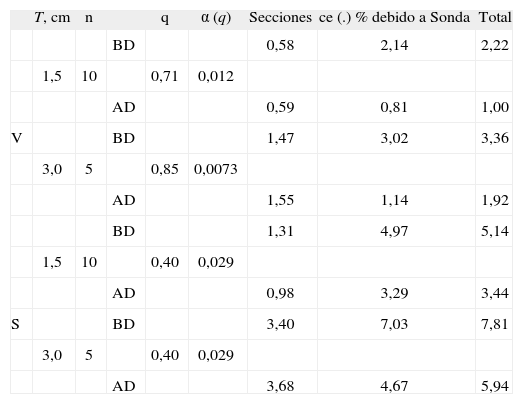
Con objeto de completar las tablas 1 y 2, indicamos a continuación cómo predecir la variancia debida al muestreo. A veces, es también interesante estimar las contribuciones a la variación total, por un lado de las secciones sistemáticas y por otro de los puntos o intersecciones contados en cada sección (los resultados correspondientes se recogen en la tabla 3). El procedimiento es algo prolijo, y por ello nos limitamos a indicar las pautas y la bibliografía donde pueden consultarse las fórmulas y los ejemplos numéricos pertinentes. Sin necesidad de familiarizarse con los detalles, los resultados recogidos en las tablas 1-3 dan una idea de la alta precisión del muestreo sistemático. La conclusión básica es que, para un proyecto de rutina, una distancia T de 3 cm entre secciones y las sondas de baja densidad utilizadas aquí proporcionan una precisión suficiente.

Tabla 3.

Datos de la variación de los estimadores

	T, cm	n		q	α (q)	Secciones	ce (.) % debido a Sonda	Total
			BD			0,58	2,14	2,22
	1,5	10		0,71	0,012
			AD			0,59	0,81	1,00
V			BD			1,47	3,02	3,36
	3,0	5		0,85	0,0073
			AD			1,55	1,14	1,92
			BD			1,31	4,97	5,14
	1,5	10		0,40	0,029
			AD			0,98	3,29	3,44
S			BD			3,40	7,03	7,81
	3,0	5		0,40	0,029
			AD			3,68	4,67	5,94

Componentes de la variación total de los estimadores del volumen cerebral (V) y de la superficie pial (S) para dos densidades de secciones y de sondas.

BD, AD: baja y alta densidad de sonda, respectivamente, véanse tablas 1 y 2; n: número de secciones; q: constante de suavidad de la función de medida; T= distancia entre secciones; α(q): factor correspondiente para estimar el coeficiente de error (ce) (.), véase el texto.

La predicción del coeficiente de error (error típico del estimador/valor del estimador) del estimador de Cavalieri para el volumen consta de los siguientes pasos³⁴: 1) estimar la variancia debida al conteo de puntos; para ello es necesario estimar la constante B/A = perímetro medio de la traza de superficie pial por sección/raíz cuadrada del área media de la sección cerebral, como se indica en los ejemplos de la bibliografía^25,40. Aquí hemos calculado el valor 12,8 para esa constante. 2) Estimar la constante de suavidad q de la función de áreas de sección del objeto (en la referencia 35, en la ecuación (3.8), falta un signo «menos» precediendo al factor «4» en el numerador), y calcular el factor α(q) (tabla 3). Por último, 3) estimar el coeficiente de error del estimador del volumen como se indica³⁴, ecuaciones (3.6). Por otra parte, las mencionadas componentes de la variación total se estiman a partir de la ecuación (3.5)³⁴.

Es importante reseñar que, si bien q es una constante característica que sólo depende del objeto y de la orientación de corte, su estimador depende del número de secciones. En la tabla 3 se han promediado las estimaciones para 10 y 5 secciones separadamente para el volumen, y todas las estimaciones para el área de la superficie pial, por obtenerse valores parecidos en todos los casos. La ecuación (8) refleja el papel de q en la precisión de un estimador obtenido mediante observaciones sistemáticas a lo largo de un eje.

La variancia del estimador del área de la superficie pial tiene un componente importante debido al número de ángulos adoptados para las secciones verticales (fig. 1c y d)³⁶. Sin embargo, los pasos a seguir no están aún publicados en suficiente detalle. Por otra parte, en el presente ejemplo hemos utilizado solamente una serie de secciones, con lo cual no es posible estimar la variación total. Por ello, en la tabla 2 figura el debido a los efectos combinados de la variación entre secciones e intersecciones con cicloides, pero no entre orientaciones. Lo mismo cabe decir de la tabla 3. Por otra parte, no se dispone de una fórmula para estimar la variancia debida a las intersecciones con cicloides; aquí hemos adoptado el modelo de Poisson⁴¹. Es importante señalar que, si se hubiera utilizado una segunda serie perpendicular a la analizada, sería muy inferior a las dadas en las tablas 2 y 3. Con dos direcciones, en la práctica también bastaría con utilizar una distancia T = 3 cm entre secciones (que daría lugar a 4-6 secciones por serie) y la sonda de baja densidad de cicloides.

DISCUSIÓN

Consideraciones generales

La alta prevalencia de procesos neurodegenerativos cerebrales, como la demencia, en la población geriátrica, nos motiva a realizar esfuerzos que disminuyan la incertidumbre diagnóstica, mejorar el diagnóstico temprano, y poder ofrecer mejores posibilidades de atención y tratamiento de acuerdo con las necesidades del enfermo, y su familia^42,43. Un aspecto importante, la disminución de la incertidumbre diagnóstica mediante el empleo de criterios clínicos, plantea algunos problemas: sus valores de sensibilidad y especificidad en ocasiones no alcanzan el 90%; cuando se comparan los criterios estandarizados con series neuropatológicas la coincidencia no es completa y, por último, cuando se comparan criterios entre sí, con el diagnóstico clínico, la correlación puede, incluso, ser escasa^44,45. Recientemente se han desarrollado diversas técnicas diagnósticas analíticas, con resultados aceptables pero no categóricos, que también pueden ser útiles como apoyo al diagnóstico clínico de la demencia^46,47. Con todo, la demencia, en general, carece en este momento de parámetros de clasificación y diagnóstico de carácter numérico objetivo, como ocurre en otras afecciones. Sin embargo, la neuroimagen ha demostrado mejorar el rendimiento diagnóstico en la demencia, ayudando fundamentalmente en la diferenciación de procesos demenciantes neurodegenerativos frente a procesos de origen vascular⁴⁸, y es una de las pruebas recomendadas como rutinarias en las guías de práctica clínica de la demencia^9-11. Una ventaja adicional de la neuroimagen es la posibilidad de realizar análisis volumétricos que pueden aportar datos objetivos de tipo numérico de las estructuras encefálicas. Todo esto indica la necesidad de lograr un mayor desarrollo de la morfometría cerebral, así como una mayor homogeneidad de las técnicas empleadas para cuantificar la neuroimagen, que actualmente son muy variadas. El límite teórico de la precisión de las mediciones de la neuroimagen viene determinado por la capacidad de discriminar dos puntos contiguos por el propio equipo de obtención de la imagen⁴⁹. Sin olvidar, no obstante, que en el análisis de los sujetos vivos también influyen en la precisión los movimientos, involuntarios o patológicos; el espesor del corte del cerebro, si en un voxel coinciden señales de dos tipos diferentes de tejido⁵⁰, así como otras cuestiones relacionadas con el campo magnético, el área de visión, la calibración, etc.

La volumetría cerebral con el método de Cavalieri como instrumento de estimación de la atrofia cerebral en la demencia

Existe para el estudio del cerebro una amplia variedad de metodologías que se utilizan para la cuantificación morfométrica del encéfalo in vivo⁵¹. Mediante imágenes de RM se analizan volúmenes de estructuras clave en la demencia como el hipocampo⁵² o el grado de atrofia cortical mediante planimetría semiautomatizada, o bien mediante el trazado de los bordes de las estructuras de interés⁵³. Recientemente la estereología, mediante la aplicación del método de Cavalieri, en combinación con el recuento de puntos, se emplea para la estimación de volúmenes de estructuras como los ganglios basales, el hipocampo, la amígdala y los ventrículos cerebrales^23,54.

Las evaluaciones volumétricas mediante el método trapezoidal que se enseña en cálculo numérico tienen en común la presencia de un residuo, que viene a ser un sesgo, y que disminuye sin desaparecer cuando la distancia entre observaciones se reduce. Visto así el estimador de Cavalieri —que puede ser el estimador de una integral (en este caso la integral de la función de áreas de sección, que es el volumen del objeto)— parece bastante rudimentario en comparación con las técnicas de integración numérica. Pero existe una distinción importante: la malla donde se efectúan las observaciones es aleatoria, y como consecuencia el residuo medio, es decir, el sesgo es cero para un número de observaciones cualquiera. La medición insesgada es una propiedad de gran valor en biología, porque a menudo la precisión es fácil de aumentar indefinidamente intensificando el muestreo. Es de destacar que la componente de la variancia del estimador de Cavalieri debida a la variación entre secciones sistemáticas sigue la ley asintótica:

donde el subíndice s indica debida a secciones, n es el número de secciones y q es la constante de suavidad del objeto mencionada en la sección «Precisión de los estimadores». Nótese que por muestreo aleatorio simple el denominador de la ley análoga es simplemente «n». Por ejemplo, si q = 1, entonces n = 4 secciones de Cavalieri «hacen lo mismo» que 256 secciones independientes^26,55. Algo parecido ocurre con la estimación de áreas mediante conteo de puntos. Una vez más, el método parece rudimentario en comparación con la «determinación» prácticamente «exacta» basada en el conteo exhaustivo de píxeles. Si las regiones de interés son susceptibles de segmentación automática rápida (es decir, sin laboriosas correcciones manuales) y satisfactoria, entonces evidentemente el conteo de píxeles es ventajoso. Si, por el contrario, es necesario trazar la frontera de la imagen manualmente con un cursor, este método es totalmente desaconsejable por que es, generalmente, sesgado y enormemente menos eficiente que el conteo de puntos. Típicamente un conteo de 200-400 puntos en total (es decir, entre todas las secciones) aporta una precisión suficiente en el presente contexto.

Se ha podido determinar que la precisión de la cuantificación del volumen, con el método de Cavalieri, de diversas estructuras corporales empleando RM es bastante exacta. No se aprecian desviaciones importantes entre las medidas de volumen corporal comparado con la determinación del mismo por inmersión en líquido⁵⁶. Lo mismo ocurre con el volumen de orina almacenado en la vejiga comparado con el volumen de orina en la micción completa⁵⁷, o con el volumen estimado de un feto a término y el volumen determinado en el posparto asumiendo una densidad neonatal de 1 g/cm³⁵⁸.

Respecto a una estructura clave en la demencia como es el hipocampo, se ha demostrado que su volumen disminuye en diversas afecciones, y en la demencia se puede comprobar una atrofia del 40% en ancianos con enfermedad de Alzheimer⁵⁹, así como su disminución progresiva en estudios longitudinales de pacientes con demencia⁶⁰. La variancia en las estimaciones del volumen hipocámpico se debe a la propia variación biológica como al hecho de que el volumen es estimado más que medido realmente.

Puesto que el cuadrado del coeficiente de variación entre los estimadores de los volúmenes de un población es igual al cuadrado del coeficiente de variación biológico más la media de los cuadrados de los CE de las estimaciones de volumen debidos al muestreo, y dado que este último se puede aproximar con fórmulas adecuadas, mientras que el primero se observa directamente, es posible calcular la magnitud de la variación biológica. Por tanto, se puede optimizar tanto el número de secciones como la densidad de las sondas (nubes de puntos) al definir previamente que precisión deseamos en la estimación del volumen hipocampal de cualquier otra estructura cerebral⁶¹.

Con el uso generalizado de métodos de rastreo no invasivos, como la RM, el uso de las técnicas descritas en el presente artículo está cobrando, desde hace unos años, un renovado interés. Una cuestión central es si una sección del córtex cerebral adquirida mediante RM ofrece la misma área de sección que una sección física en la misma posición. Recientemente se comparó el estimador de Cavalieri del volumen de diversos compartimentos cerebrales mediante ambos tipos de secciones. El estudio reveló una aparente discrepancia en el estimador del volumen de la corteza³⁴; este problema, que se hace extensible a la estimación de la superficie pial, permanece abierto y será objeto de estudios posteriores en los próximos años.

La estimación estereológica de la superficie pial cerebral como posible nuevo estimador de la atrofia cerebral en la demencia

Aunque la cuantificación y el posterior seguimiento en el tiempo de los parámetros morfométricos cerebrales se están utilizando para establecer pronósticos de carácter evolutivo en el deterioro cognitivo leve (conversión en enfermedad de Alzheimer o bien estabilización mantenida durante años^62-64), todavía carecemos de marcadores morfométricos cerebrales estandarizados. Uno de esos posibles marcadores es el área pial superficial de la corteza cerebral.

En los cortes verticales de RM tiene una importancia indiscutible la cuantificación de la atrofia cortical⁶⁵, que está muy plegada sobre sí misma, de forma que dos tercios de su superficie se encuentran en la profundidad de los surcos y cisuras cerebrales, por lo que su medición no es sencilla. En muchas ocasiones el grado de atrofia, tanto cortical como subcortical, es una apreciación subjetiva debido al crecimiento del sistema ventricular y al ensanchamiento de los surcos y cisuras cerebrales⁶⁶. De los sistemas más objetivos que se emplean para cuantificar la atrofia cerebral superficial, ninguno cumple el requisito del muestreo isotrópico necesario para la estimación insesgada de una estructura tan irregular como el área superficial de la corteza cerebral. Por tanto, esta estimación, el área de la superficie pial cerebral, es un problema controvertido. Como se ha expuesto, es frecuente encontrar estudios que analizan aspectos relacionados con la volumetría en los pacientes con demencia centrados en hipocampo, volumen cerebral total y volumen ventricular; sin embargo, no es habitual el empleo de la atrofia cortical como marcador. Ocasionalmente se ha evaluado el grado de atrofia contrastando las diferencias de relación entre volumen cerebral/volumen craneal en ancianos normales y con demencia⁶⁷. Más recientemente se evalúa el grado de atrofia mediante la cuantificación de la sustancia gris cortical empleando la técnica de morfometría basada en el vóxel (MVB) frente a otras metodologías⁶⁸. Con la proliferación de distintos programas informáticos de reconstrucción de objetos a partir de secciones seriadas existe una opinión bastante generalizada de que en estos casos la superficie es directamente accesible, sin necesidad de recurrir al método estereológico. Una de las estrategias consiste en intentar aplicar una ecuación análoga a la (1). Sin embargo, este enfoque es erróneo. No hay forma de corregir la suma de los perímetros de las secciones para obtener el área de la superficie correspondiente. Desafortunadamente, el método de Cavalieri no es válido para superficies. Otra estrategia puede ser descomponer la superficie en una malla de triángulos u otros polígonos, y sumar las correspondientes áreas. Aquí nos topamos con el problema de que con distintas mallas la mencionada suma convergerá, en general, a valores diferentes cuando el área de los polígonos tiende a cero. En algunos casos, no es ni siquiera claro que el límite de la suma sea finito. El único método insesgado y general de que disponemos para estimar el área de una superficie está basado en el número de intersecciones entre la superficie y una recta IUR que la corta. En este artículo hemos descrito, sin entrar en demasiados detalles, un diseño insesgado, altamente eficiente y sencillo de aplicar, que es el diseño vertical combinado con cicloides. Aunque aún no se han publicado estudios completos sobre la precisión del estimador (7), en la práctica se pueden adoptar series verticales de Cavalieri mutuamente perpendiculares, con un número de secciones por serie que varían entre 5 y 10, y un número de intersecciones entre 150 y 300 por serie (es decir, de 300 a 600 intersecciones en total).

No hay datos en la literatura científica sobre la evaluación de la atrofia cerebral en ancianos con demencia, cuantificando el área superficial de la corteza cerebral. Como hemos visto, la estereología conforma una herramienta sencilla y eficaz, capaz de proporcionarnos una cuantificación numérica y objetiva de los volúmenes y la superficie cerebral, o de las áreas y regiones de nuestro interés⁶⁹, que ayuda a la evaluación diagnóstica, evolutiva y pronóstica de los pacientes ancianos con demencia. Su medición mediante procedimientos estereológicos es una técnica de realización sencilla que, posiblemente, aportará datos relevantes, tanto en el envejecimiento cerebral normal como en el patológico. Por este motivo, la estimación del área superficial de la corteza cerebral mediante la estereología aporta datos insesgados que podrían emplearse como un marcador más en la enfermedad de Alzheimer y otras demencias y así poder realizar un diagnóstico temprano más objetivo.