DNA test evaluation in large-scale identification cases of missing persons

Abstract

The evaluation of the DNA test in massive identification cases requires the use of Bayes’ Theorem to estimate the probability of identification from a priori data together with probabilities obtained from the DNA test itself. To apply it, one needs to specify the prior probabilities of the hypotheses. An interdisciplinary team and an identification coordinator are key stakeholders in this process. The statistical approach can be complex but there exists validated non-commercial software, such as Familias, which aid in estimating the likelihood ratios of the DNA test for the given hypotheses. Next, the posterior probabilities in massive identification events can be estimated using the one to one, PM-driven, AM-driven, or Global approaches published recently by Kling et al. (2021) which are discussed in this article. The Identification Coordinator has a key role in formulating the hypotheses of the case, in establishing the prior probabilities, the identification threshold, and in consolidating the integrated identification report together with the multidisciplinary team through the reconciliation of the case.

Resumen

La valoración de prueba de ADN en casos de identificación masiva exige el uso por los peritos del teorema de Bayes para estimar la probabilidad de identificación a partir de unos datos a priori a los que suman las probabilidades proporcionadas por la prueba de ADN. Para aplicarlo hace falta por una parte especificar la probabilidad a priori de las hipótesis de identidad que se pueden plantear de modo que un equipo multidisciplinario y la figura de un coordinador de identificaciones son clave. El abordaje estadístico puede ser complejo pero existen programas validados no comerciales, como el software Familias que facilitan las estimas de las razones de verosimilitud de la prueba de ADN para las hipótesis que se establezcan. A continuación la probabilidad a posteriori en eventos de identificación a gran escala se puede estimar a través de las aproximaciones one to one, PM-driven, AM-driven y Global approach publicadas recientemente por Kling et al. (2021) y que son descritas en detalle en este artículo. El papel del Coordinador de Identificación es clave en la formulación de las hipótesis del caso, en el establecimiento de las probabilidades a priori, del umbral de identificación y en consolidar el reporte integrado de identificación junto al equipo multidisciplinario a través de la reconciliación del caso.

Introduction

DNA testing is a fundamental tool in mass victim identification;^1–3 however, it is not the only test to consider in these scenarios. Traditionally, the results of genetic analysis for forensic purposes have been accompanied by a statistical assessment to measure their significance. The likelihood ratio (LR) is used to compare 2 alternative hypotheses and is generally used to assess the results of genetic testing^4,5 without taking other information into account. Its value therefore depends only on genetic data (allele frequencies,⁶ degree of compatibility between the profiles to be compared, quality of the genetic profiles, etc.).

However, 2 genetic profiles being compatible (e.g., they share one allele in each marker) does not mean that they have to come from a parent and their child. In a scenario involving multiple victims, a multitude of comparisons need to be made of genetic profiles from the deceased (postmortem [PM] profiles) with genetic profiles from relatives or personal belongings of missing persons (antemortem [AM]). In this massive context, apparent genetic matches can be found without there necessarily being a family relationship between the sample donors, especially if the genetic profiles are partial. Additional information is necessary to achieve identification, as a genetic match does not mean that we have directly identified a victim. In other scenarios where DNA testing is useful (e.g., in criminal investigations), it is the judicial authority who will incorporate the value of the LR with other non-genetic evidence to reach a final conclusion. But in mass identification cases, experts from different areas usually decide on the final result; reporting an LR value is not sufficient for that purpose, as it does not report the final likelihood of identification, the so-called posterior probability. This comes from Bayesian statistics. However, this theorem is not easy to apply in that it allows combining non-genetic information about the case with genetic information. Therefore, we need to establish what the prior probability of identification is before DNA analysis.

Large-scale identification processes occur as a consequence of mass disappearances related to armed conflicts, natural disasters, violations of human rights, or international humanitarian law, among others. These cases can overwhelm local forensic services, requiring procedures and practices to be adapted.^7–9 This adaptation ranges from capacity building and management of corpses and forensic information to hypotheses of identity, statistical approach, and assessment of DNA evidence.

Today, in many medico-legal systems that perform large-scale identifications of victims and missing persons, genetic experts still work in isolation from other forensic specialties, and continue to use default prior probability values. One of the most common errors is to apply a value of .5 probability (50%), classically applied in paternity tests, although of very debatable use in judicial evidence. In this article, we address the importance of understanding identification as a multidisciplinary task and the risks of not using adequate prior probability in mass identification cases.

Bayes theorem in cases of mass identification

To calculate an LR, at least 2 hypotheses about the facts need to be stated. The hypotheses must be mutually exclusive (if one is true, the other must be false), for example:

H₁ = The skeletal remains belong to a child of P and M.

H₂ = The skeletal remains do not belong to a child of P and M.

The LR measures the probability of having attained the genetic profiles that were obtained in the skeletal remains, and in P and M (whatever this result is; i.e., whether they share alleles or not) under the 2 hypotheses mentioned. And it is formulated as follows (1):

where E = evidence (the genetic result in the simples analysed), P = probability and the symbol "|" = assuming.

The results obtained in the analysis may support one or another hypothesis, depending mainly on whether or not the genetic profiles are compatible with each other and on the frequency of shared alleles. The LR can take values between 0 and infinity. Under the usual assumption of independence between markers, the LR for the genetic profile is obtained by multiplying the LRs of each marker. If the value is below 1, the genetic results are more supportive of the denominator hypothesis, usually the one that assumes no relatedness. If the LR value is 1, the genetic results do not support one hypothesis over the other, i.e., the genetic evidence is neutral. A clear example of this situation is when no results have been obtained for some genetic marker, in which case the LR for this marker is 1. If the LR value is greater than 1, the genetic results are more supportive of the numerator hypothesis, and more so the higher the value than 1.¹⁰

The LR value obtained in the DNA test can be incorporated with other non-genetic information to calculate the posterior probability of identification by applying Bayes' theorem. Its formulation is simple when there are only 2 hypotheses to test (2):

P(H₁ | E) is the posterior probability of identification, i.e., the probability that is ultimately of interest to the investigator or judicial authority hearing the case. P(H₁) is the prior probability of hypothesis 1 and P(H₂) is the prior probability of hypothesis 2. P(E | H₁) and P(E | H₂) were defined earlier in the LR. Therefore, the posterior probability is a combination of the LR and the prior probability, and answers what the probability of a hypothesis is given the data (the genetic and non-genetic evidence). Bayes' theorem can also be expressed with odds. Annex 1 of the supplementary material shows how the 2 forms of the theorem are related.

Returning to the form defined in (2) of the theorem, if P(H₁) is .5; and therefore P(H₂) will also be .5, the formula simplifies (3):

And if we divide the numerator and denominator of (3) by P(E | H2), we get the famous formula commonly used in paternity cases to calculate the posterior probability (4):

However, in cases of mass identification, we are confronted with many more hypotheses; e.g., in the case of mass grave finds we must test a set of hypotheses and not just 2 as in isolated identification cases. Kling et al.,⁶ give the example of a simple scenario of a mass grave in which 3 bodies are found (V1, V2, and V3) and 3 families are looking for 3 missing persons (F1, F2, and F3). The hypotheses to be tested would be:

H₁ = V1 belongs to family F1.

H₂ = V2 belongs to family F1.

H₃ = V3 belongs to family F1.

H₄ = Another unknown victim belongs to family F1.

H₄ contemplates that the missing person that family F1 is looking for is not actually in the set of human remains investigated. In the case of families F2 and F3, the hypotheses would be the same as for F1, but replacing F1 by F2 and F3, respectively.

In cases with multiple hypotheses, the application of Bayes' theorem to calculate the posterior probability is formulated as follows (5):

Where P(H_i) is the prior probability of identification for the hypothesis of interest and the summation ∑_j=1^kP(E | H_j)P(H_j) indicates the sum of the hypotheses 1 to k. In our example, if the hypothesis of interest were H₁, the formula (5) would be expressed (6):

We can simplify this formula (6) by dividing the numerator and denominator by the term P(E | H₄). This will give us (7):

The value of LR₄ is 1, as it was obtained by dividing P(E | H₄) / P(E | H₄). And if in addition the value of the prior probability is equal for all hypotheses, we can simplify further. Suppose that in this case P (H₁) = P(H₂) = P(H₃) = P(H₄) = 1/4 (see next section on prior probabilities). We then obtain (8):

So far, we have seen that there is a large difference between applying Bayes’ theorem in scenarios with only 2 hypotheses and in scenarios with k hypotheses. We will now focus on what happens in massive scenarios when Bayes’ theorem is applied. For this, we refer again to Kling et al.,⁶ who describe different approaches to setting the hypotheses. In this section, we only describe the different ways of approaching the problems, but in section 4, the reader will see how each of them is applied in more detail with a simple example. The different approaches include:

• a)

  One-to-one: this approach is usually applied in non-mass scenarios, where there is a presumed identity, and a single PM profile is compared with a single pedigree. However, it is also applied in mass scenarios, when the PM profile is compared with all pedigrees, and finally only 2 hypotheses are considered when Bayes’. theorem is applied. The fact that only 2 hypotheses are considered does not imply that the value of the prior probability has to be .5; in section 4, the reader can see an ad hoc example. But we are now interested in the hypotheses:

  H₁ = Victim 1 is related to family F1.

  H₂ = Victim 1 is not related to family F1.

• b)

  PM-driven: in this approach the hypotheses are set considering the victims, i.e., the question to be answered is: which family is related to this particular victim? This approach attempts to provide the most likely family for each victim, and does not consider that 2 different victims could be associated with the same family. The hypotheses would therefore be:

  H₁ = Victim 1 is related to family F1.

  H₂ = Victim 1 is related to family F2.

  …

  H_N = Victim 1 is related to family NF, where N is the number of families searching for their loved ones.

  H_N+1 = Victim 1 is not related to any of the N families.

• c)

  AM-driven: in this approach, the hypotheses are set considering the families, i.e., the question to be answered is: which victim is related to this particular family? It is not considered that the same victim could be associated with 2 different families. And the hypotheses are set:

  H₁ = Family F1 is related to V1.

  H₂ = Family F1 is related to V2.

  ….

  H_M = Family F1 is related to victim M, where M is the number of victims.

  H_M+1 = Family F1 is not related to any of the M victims.

The one-to-one approach is the most usual due to its simplicity, but it is not without problems. By considering only 2 hypotheses, e.g., V1 is related to F1 vs. V1 is not related to F1; the possibility that victim 1 is related to F2, F3, etc. is not considered. In other words, although the comparison has been made with all profiles, in the statistical assessment, we are only taking into account one of the results of the comparison.

However, in the PM-driven and AM-driven approaches, all comparisons are taken into account in the statistical assessment of the results, as several hypotheses are considered at the same time. However, both approaches have the disadvantage that the statistical evaluation is performed sequentially, i.e., each hypothesis is considered one at a time in the numerator of the formula (5). This can have a great influence in cases where there is more than one missing person in a family. For example, if a father P and a son H are missing and only H's mother is available as reference sample, father P cannot be identified unless H's genetic profile is elevated to the status of reference profile. Therefore, the identification in this case is sequential, first identifying the son, and once that identification is certain, the father is identified.

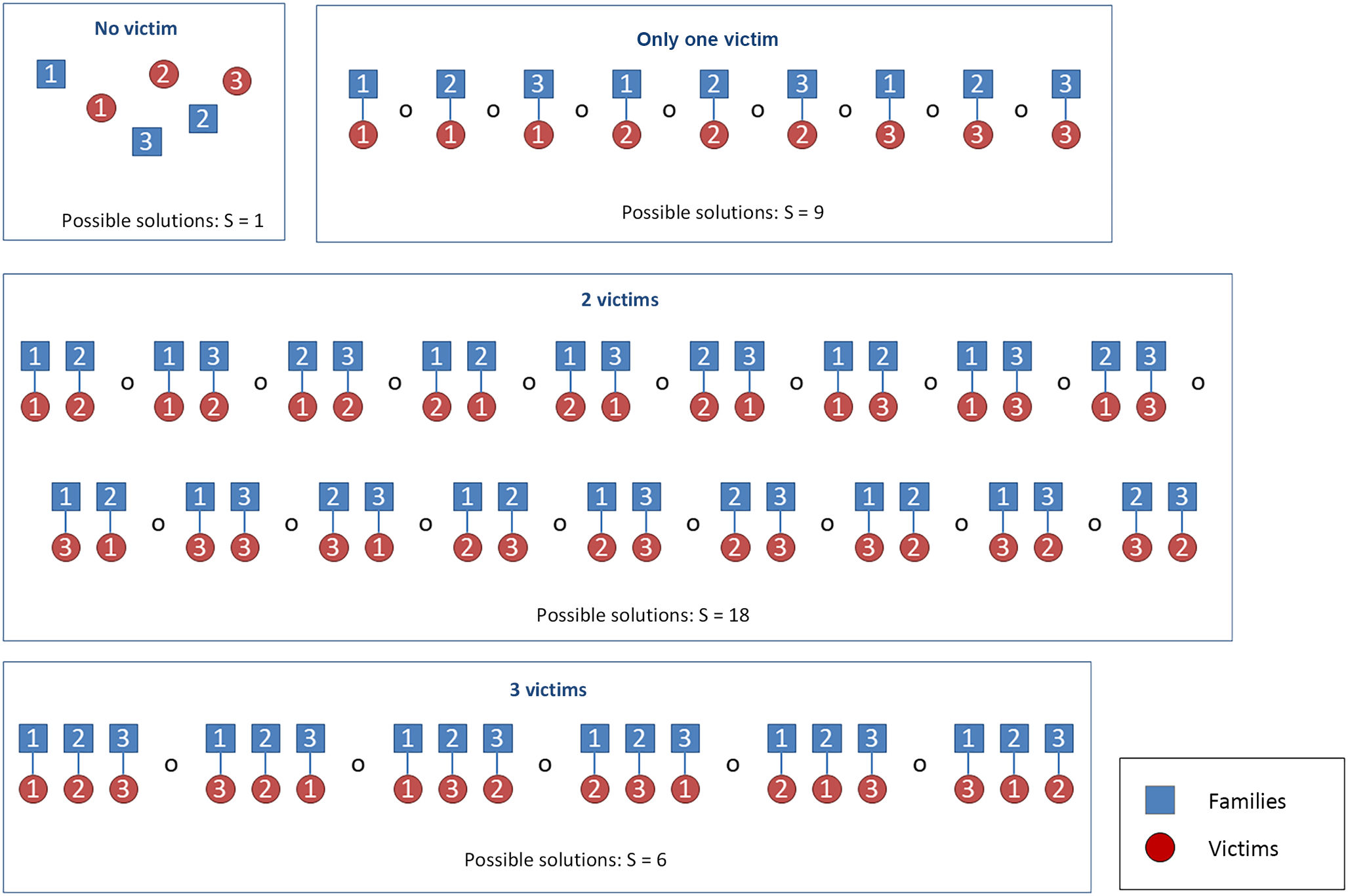
The solution to this problem is offered by the authors themselves, through what is termed the global approach, although this approach requires a great computational effort. This method considers all the possible solutions that can be obtained in the mass identification project; e.g., no victim is identified, only 1, only 2, etc. An example of possible S solutions of a case using this global approach is shown in Fig. 1. The main advantage of the method is that it is not possible to assign the same victim to different families or to assign different victims to the same family in the same position in the pedigree, as the approach considers all the results at once and not sequentially as in the other 3 approaches. There being 2 missing persons within the same family is not a problem with the global approach, as in the example above where P and H were missing, it is not necessary to upgrade H's genetic profile to an AM profile, but both can be identified at the same time.

Fig. 1.

Global approach. Scenario with 3 victims and 3 families of 3 missing persons. All the results that can be obtained (S) are shown, taking into account that it is possible that no match can be obtained:

1. No genetic match.

2. Only one match (F1 with V1, or F2 with V1, …, or F3 with V3).

3. Two genetic matches (F1 with V1 and F2 with V2, or F1 with V1 and F3 with V2, …, or F2 with V3 and F3 with V2).

4. Three genetic matches (F1 with V1, F2 with V2 and F3 with V3, …, or F1 with V3, F2 with V1 and F3 with V2).

5. The total number of possible S solutions S is 1 + 9 + 18 + 6 = 34.

6. Translated from Klingt al.⁶

Fortunately, there is free software to help us use any of these approaches to the problem. The Familias¹¹ programme provides the necessary tools to define the hypotheses according to the AM-driven, PM-driven, and one-to-one approaches. Recently, Vigeland and Egeland¹² have developed a package for R called "dvir" to approach the problem from a global perspective (global approach, called joint approach in their publication).

The prior probability of identification

The prior probability of identification is the belief that an unidentified deceased person may belong to a certain family. It is a subjective probability, but can be based on certain data.

One of the most common mistakes when setting the value of the prior probability of identification in mass scenarios is to apply the same value used in paternity tests (50%). Usually, the expert geneticist does not have any non-genetic information from the paternity case to establish a prior probability value and, almost more out of tradition than accuracy, experts sometimes use the value of 50%.

It is believed that a probability of 50% is uninformative, as the probability of paternity is given the same value as the probability of non-paternity (100%-50% = 50%). However, this is not the case. By applying a prior probability value of 50%, we are assigning a 50% probability of paternity to the alleged father, and the remaining 50% is distributed among all the males in the population of interest, and therefore a higher probability is assigned to the alleged father than to each of the other possible fathers.⁶ Also in cases of judicial paternity, it is the judge who should set the value of the prior probability, and in this sense, the expert is overstepping their role.¹³

It should also be noted that if we apply a prior probability of 50% and contrast 2 hypotheses (related vs. unrelated), in cases of mass identification, we only need a value of LR = 1000 to reach a posterior probability of 99.9%, and with an LR = 10 000 we will reach a value of 99.99%. These posterior probability values can lead a judge to determine the identification with high certainty, however, a value of LR = 1000 can be achieved even if the genetic match is not a true genetic match.

As we mention above, a match between genetic profiles is not synonymous with identification. Let us imagine that in the analysis of a mass event, we find a match between the PM genetic profile obtained from skeletal remains and the AM genetic profile of a 10-year-old child looking for his father. It could happen that this compatibility is false, especially if there are many individuals involved or the PM genetic profiles are partial. If the anthropologist determines that the skeletal remains in question come from a sub-adult individual, the match can clearly be given as false, as the prior probability in this case would have a value of 0, since the age of the individuals precludes their having a parent–child relationship. Unfortunately, it is not possible to reach such clear conclusions in all cases.

Traditionally, mass scenarios have been classified as closed or open. In closed cases, the number of missing people is usually quantifiable, and their identity is known. The typical example is a plane crash where there is a list of passengers, although this may not be 100% reliable. In open cases, the actual number of missing persons may be unknown, i.e., their estimation is more uncertain. In real life, however, it is more common to find mixed cases, i.e., cases where the identity of some of the missing persons is known, but not all of them.¹⁴

If there is no other information, the number of missing persons is usually taken into account to establish the prior probability of identification.¹³ Thus, in the case mentioned in the previous section, where the number of missing persons was 3, the prior probability could be set at 1/4 (1/[n° missing persons + 1]), in order to assume that the person we are looking for may not be in the grave under investigation. This approach assumes that all victims have the same prior probability of identification (flat priors). And the probability of non-identification for each individual would be 3/4. The reader can find examples in the exercises by the Spanish and Portuguese Speaking Working Group of the International Society for Forensic Genetics (GHEP-ISFG).^15,16

The prior probability of identification can be redefined by other experts such as anthropologists, taking into account other characteristics such as sex or age. If in the case of the 3 missing persons, 2 are women, and the human remains to be identified still present physical characteristics that make their female sex visible, one could then redefine the above prior probability to 1/3 (1/[n° missing women + 1]). However, we should not forget that there can also be uncertainty in determining the age or sex of human remains, especially if we are faced with a scenario of incomplete skeletal remains. For example, age estimation in PM remains may not be very accurate depending on the age of the individual, as occurs when the morphology of the pubic symphysis is considered in individuals over 40 years of age.¹⁷

Other characteristics such as tattoos, marks, prostheses can be more difficult to quantify. The statements of witnesses who may have been present at the events can also be considered, but they are also difficult to quantify and may even be unreliable. ¹⁸ In Budowle et al.,¹⁹ the reader can find a discussion of the problems that can arise when 100% credibility is given to witness statements, other information (location of the grave, PM interval, demographic variables) or when potential dependence between the different variables used to establish the prior probability of identification has not been taken into account.

To define the prior probability, Gill etal.,²⁰ looked at the work conducted on the dental pieces of the skeletal remains that were later identified as belonging to the Romanov family. An example of how to apply Bayesian thinking to identification can also be found in King et al.²¹ The reader will see that sometimes non-genetic information is difficult to quantify. The frequency of various characteristics or conditions is not precisely known, and therefore the prior probability value is difficult to estimate.²²

Therefore, in conclusion, the estimation of prior probability considering the number of missing persons is usually conservative and defensible. Estimates can be made even when the exact number is not known. For example, in the terrorist attack on the World Trade Centre in 2001, a prior probability of 1/3000 was used because the number of missing persons was estimated at slightly less than 3000.²³ This estimate (estimated number of missing persons) is the most appropriate estimate in large-scale identification cases, for DNA laboratories to report the list of possible identifications that can be corroborated or ruled out after including non-genetic information.

Calculating the posterior probability: an example and different approaches

In this section, we return to the simple example of Kling et al.⁶ where we have a scenario with 3 victims (V1, V2, and V3) and 3 families (F1, F2, and F3) each searching for a missing person (MP1, MP2, and MP3). Based on the heading on the value of the prior probability, we will say that for each victim V_i, the value of this probability is 1/4, thus considering the possibility that the victim we are looking for is not in the investigated scenario.

Let us assume that after the genetic analysis and comparing the profiles we obtain the results described in Table 1. The LR value has been calculated taking into account each identity hypothesis against the hypothesis that considers the absence of family relationship (in our example, H₄). Strictly speaking, the LR value should not be 0 if we consider the possibility of mutation, but we approximate it to 0 to simplify the calculations.

Table 1.

Practical assumption of a scenario with 3 victims and 3 missing persons. The results are shown after comparing the postmortem genetic profiles with the antemortem genetic profiles

Victim	Family	LR
V1	F1	10^6
V1	F2	10
V1	F3	0
V2	F1	500
V2	F2	0
V2	F3	0
V3	F1	0
V3	F2	0
V3	F3	0

We now show how posterior probabilities are calculated with the one-to-one, PM-driven, and AM-driven approaches.

One-to-one

With this method we only consider 2 hypotheses, which in view of the results would be:

H₁ = V1 is related to family F1.

H₂ = V1 is not related to family F1.

The results obtained in the other comparisons, i.e., other candidate matches. The posterior probability would be calculated according to the formula (2), considering that if the prior probability of identification has a value of 1/4, the probability of non-identification will be 1-1/4 = 3/4. But for simplicity, as we already have LR values, we can use the formula (7) with only 2 hypotheses:

In Annex 2 of the complementary material, you can see the same example, but applying Bayes’ theorem in the form of a bet.

PM-driven

In this approach, a victim is compared with each of the families. In our case we would say, e.g., for V1:

H₁ = V1 is related to family F1.

H₂ = V1 is related to family F2.

H₃ = V1 is related to family F3.

H₄ = V1 is not related to any of the 3 families.

The posterior probability would be calculated according to the formula (5), but we can use the simplification,⁸ as the prior probability values are equal. This gives us:

Annex 3 of the complementary material shows all the posterior probabilities for each hypothesis and for each victim.

AM-driven

In this approach, a family is compared to each of the victims. The hypotheses in our example would be, for F1:

H₁ = Family F1 is related to V1.

H₂ = Family F1 is related to V2.

H₃ = Family F1 is related to V3.

H₄ = Family F1 is related to another unknown victim.

The posterior probability would be calculated according to the formula (5), but we can use the simplification,⁸ as the prior probability values are the same. This gives us:

Annex 3 of the complementary material shows all the posterior probabilities for each hypothesis and for each family.

Global approach

As shown in Fig. 1, in this case all possible solutions are considered at the same time: no victim is identified, only 1 victim is identified, 2 are identified, and 3 are identified. In our example, there are a total of 34 possible solutions, i.e., 34 possible.

In our example, there are a total of 34 possible solutions; i.e., 34 different hypotheses. This give us:

H₁ = V1, V2, and V3 are neither MP1, MP2, nor MP3.

H₂ = V1 is MP1, V2 and V3 are neither MP1, MP2, nor MP3.

H₃ = V2 is MP1, V1 and V3 are neither MP1, MP2, nor MP3.

…

H₁₁ = V1 is MP1 and V2 is MP2, V3 is neither MP1, MP2, nor MP3.

…

H₂₉ = V1 is MP1, V2 is MP2 and V3 is MP3.

…

H₃₄ = V1 is MP3, V2 is MP2 and V3 is MP1.

Table S3 in Annex 3 of the supplementary material shows all these possibilities, respecting the values of the LR used in the other approaches and adding values of LR = 0 for the cases that were not considered in the sequential approaches.

Applying the simplification of the formula (8), from this table, the posterior probabilities of individual identification can be calculated, taking into account each hypothesis involving a particular victim. For example, for V1, the numerator considers all LRs in which MP1 appears in column V1 of the Table. The denominator is the sum of all RLs. This gives us:

Table S4 in Annex 3 of the supplementary material shows all individual posterior probabilities for each victim.

Role of the identification coordinator in the analysis of large-scale cases

While in criminalistics or paternity cases, it is the judge who determines the prior probability, in large-scale disappearances the identification coordinator should play a key role in formulating the hypothesis of the case, establishing the prior probabilities, the identification threshold, and consolidating the integrated identification report together with the multidisciplinary team through the reconciliation of the case. The Public Prosecutor's Office does not act in all countries when a disappearance occurs. In countries where disappearances are continuous over time (e.g., Mexico), or in an armed conflict of long duration (e.g., Colombia), competent authorities called National Search Commissions have been established, which play a crucial role in the investigation of cases, and therefore in the establishment of prior probabilities, taking into account at all times the suggestions of the multidisciplinary team led by the identification coordinator.

The threshold for reporting a genetic match should be set in a way that strikes a balance between maximising identifications and minimising false identifications.²⁴ Genetic laboratories usually set posterior probability thresholds of 99.90%, 99.95%, or 99.99% for reporting a particular genetic match to the identification coordinator. A value of 99.95% posterior probability means that they are willing to assume that one in 2000 genetic matches is false.²² Similarly, with a value of 99.90% it is assumed that 1 in 1000 matches will be false; and for 99.99%, there is expected to be 1 false match in 10 000. In exceptional cases, it may not be necessary to reach the posterior probability threshold to report a match of genetic data to the identification coordinator. For example, imagine a totally closed event in which the presumed identity of 4 individuals located in a grave is known, although it is unknown to whom each of the bodies belongs. If only mitochondrial DNA data has been obtained (therefore with moderate LR values), but the 4 haplotypes are totally different and each of them matches each of the 4 families searching for their loved one, this information that can lead to the identification of the individuals should be made available to the coordinator.

Discussions led by the identification coordinator on the reconciliation of a case are an essential step during the identification process where all information pertaining to the unidentified deceased person (PM) is compared and evaluated with all information pertaining to the missing person (AM). This is to be able to: i) reach a formal identification, or ii) determine the steps required to achieve an identification.

In this regard, before the reconciliation meeting takes place (and especially in cases of skeletal remains), the identification coordinator, once they receive a preliminary match of the case from the forensic genetics specialists, then corroborates the AM and contextual information checking consistency with the hypothesis of identity. Likewise, all specialists involved in the phases of the PM analysis process must confirm that all efforts, site visits, investigations, and collections of case information and other diligences have been completed, and then proceed to prepare the case reconciliation plan.

In addition to the archaeological, anthropological, odontological, and medical information that is part of the PM information, the following genetic information is discussed in reconciliation meetings for cases associated with large-scale disappearances: minimum number of individuals per DNA (in mixed cases), analysed samples that reached a profile suitable for hereditary–biological kinship analysis and/or for intra-skeletal association, biological reference samples belonging to relatives used in the analysis, obtained likelihood ratio (LR), prior probability used during the case and its basis, posterior probability obtained after the analysis, available family tree of the missing person that was not used in the comparison and assessment of the presence of other missing persons in the same family tree.

If consistency is observed after evaluation and comparison of PM data obtained from the investigations corresponding to each of the specialties (including genetics) in relation to the AM information (including the circumstances of the disappearance and other investigative information), and no unexplained discrepancies are found, then the identification is concluded. If, however, discrepancies are found in the reconciled information, additional recommendations are made (e.g., confirmation with additional reference samples or more markers, additional investigative information, additional anthropological analysis, etc.).

Conclusions and recommendations of forensic genetic analysis in large-scale identification cases

• •

  Large-scale identification processes require procedures to be adapted including adjustments in information management. Expert geneticists need specialist training in forensic statistics and appropriate software handling.

• •

  Part of these DNA procedures include posing multiple hypotheses of identity as well as the estimation of prior probability based on context information. It is recommended that in the absence of further context information, the prior probability can be estimated from the number of missing persons associated with an event.

• •

  Bayes' theorem is one of the tools that provides a comprehensive analysis in large-scale identifications, because multiple hypotheses can be integrated, including the possibility that the victim being sought is not in the investigated scenario. Applying this theorem, both genetic and non-genetic information can be considered. The posterior probability in large-scale identification events can be estimated using the one-to-one, PM-driven, AM-driven, and global approach.

• •

  For the correct statistical approach, there are free technological tools such as the Familias software that works in conjunction with packages developed in the R programming language.

• •

  In large-scale identification events, the identification coordinator must play a key role in formulating the hypotheses of the case, establishing the prior probabilities, the identification threshold, and consolidating the integrated identification report together with the multidisciplinary team through the reconciliation of the case.

Funding

None.

Conflict of interests

The authors have no conflict of interests to declare.

Acknowledgements

We would like to thank Thore Egeland for the valuable comments received during the preparation of this article.