REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Páginas 15 a 31
Enero-Marzo 1998
Artículo15E. Hidalgo Callejas. Socio CKCh n.° 44
Análisis crítico de la regla convexocóncavaDirector de la Escuela
de Kinesiología de la
Universidad de Chile
y profesor jefe asignatura
de Técnicas KinésicasCorrespondencia:
Ramón Fernández Cervantes
Escuela Universitaria
de Fisioterapia
Campus de Oza
15006 La Coruña
RESUMEN
En artrokinemática existe una relación entre rodadura y deslizamiento que según sea la forma de la articulación tiene rangos y direcciones distintas. La aplicación de la regla convexocóncava a las diferentes articulaciones y sus planos de movimiento tiene una enorme aplicación a las terapias manuales.
Su conocimiento es básico para comprender el
«porqué» de la movilización en un sentido y no en otro. Aporta la base científica a la terapéutica manual.
El presente trabajo nos define la regla CC y su base física mecánica; luego, cómo se comporta en cuatro articulaciones tipo, lo que permite extender sus resultados a las demás articulaciones según la clasificación articular.
Es un trabajo de análisis intelectual en torno a la correcta aplicación de la física a la mecánica del aparato osteoarticular.
Se usaron huesos humanos de raza blanca y origen larinoamericano.
Finalmente se ofrecen al lector los parámetros que deben tenerse presentes para la correcta aplicación de la regla convexocóncava a las terapias manuales.
PALABRAS CLAVE
Artrokinemática; Física mecánica; Regla
convexocóncava; Terapia manual.
ABSTRACT
In artrokinematic there is a close relation between rolling and sliding which according to joints it has order and different distances.
The application of the convexo-concave rules to different joints and their surface of movement have extended applications in manual therapy. This knowledge is basic for under standing the reason of why it has one movement and not another. This contribution is the base of manual therapy.
The present work defines the rules of convexo-concave and its physical and mechanic arguments; then, how it works in four joints that let the spreading out of their effects to other joints according to its classification.
This analysis about the right application of the physics into the mechanics of system. Experience human bones of white for this latin americans were used.
Finally, we offer to our readers parametres that must be present for the correct application of the rules for manual therapy of convexo-concave.
KEY WORDS
Artrokinematic; Mechanics physics; Convexo-concave rules; Manual therapy.
Revista Iberoamericana de Fisioterapia
y Kinesiología 1998;1:15-31
INTRODUCCIÓN
La regla convexocóncava es de vital importancia en el análisis biomecánico de los métodos de terapia manual.
Han sido motivo de su estudio por los más renombrados creadores de las diferentes modalidades de terapias manuales: Kaltenborn (1), Paris (2) y M. MacKenzie (3).
Su aplicación a las diferentes articulaciones del cuerpo humano empezó a hacerse masivamente, casi indiscriminadamente. Del análisis biomecánico de cada articulación se concluye que no es posible su plena aplicación a todos los casos, según ha comprobado el autor del presente trabajo. Ello motivó hacer un trabajo de investigación muy personal en el que, partiendo de una visión bibliográfica de los 2 últimos años, se hace el propio análisis biofísico partiendo del estudio anatómico con huesos humanos. Se pretende ser creativo, buscando el origen físico de la regla CC y cómo funciona en cada artículación tipo: hombro, codo, rodilla y cadera. Se empezó por definirla desde la óptica de la física, qué es el deslizamiento, para luego aplicarlo a las características particulares de las superficies articulares y los planos y ejes en juego en las cuatro articulaciones ya elegidas. Revisamos lo que Kapandji (4) y Panjabi (5) han escrito al respecto desde el punto de vista biomecánico.
MARCO TEÓRICO
Precisemos primero algunos conceptos que se
usarán:
Tipos de deslizamiento
Existen dos tipos de deslizamiento:
Deslizamiento sin eje
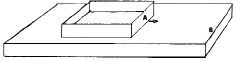
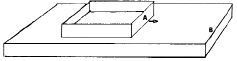
Una superficie desliza sobre otra superficie paralela, sin eje, como en la figura 1, donde el cuerpo A lo hace sobre la superficie del cuerpo B. Cada punto de la superficie A toca sucesivos puntos de B sin repetir ninguno. Desde un punto de vista de física se podría decir que existe un eje para estas «superficies aparentemente planas»; este eje corresponde a que tales superficies en realidad son curvas, pero de un radio de curvatura infinitamente ((infinity)) grande.
Deslizamiento con eje
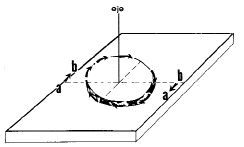
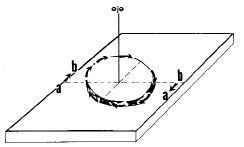
Una superficie ubicada paralelamente a otra superficie y ambas en contacto. La móvil, con un eje perpendicular a la superficie opuesta. Desliza dibujando un círculo de radio igual a «la distancia desde el centro a su arista más distante». En este deslizamiento cada punto de una de las superficies toca sucesivos puntos en círculo que se van repitiendo al ritmo de la frecuencia de giro (Fig. 2).
Los puntos deslizan en dirección opuesta en lados opuestos al eje; es decir, si en un lado dibujan un semicírculo de izquierda a derecha, en el lado opuesto al eje esos puntos se deslizan de derecha a izquierda.
Si lo analizamos desde la perspectiva del eje todos los puntos giran al mismo tiempo en igual sentido. Esta forma de deslizamiento se observa en la lijadora tipo taladro.
Congruencia
Se refiere a que el radio de curvatura anatómica de cada componente óseo (partner) tiene un grado de similitud en su módulo (su largo). Si ambos son iguales hay congruencia y ésta se perderá en la medida que cada radio se hace distinto del otro:
-- A mayor congruencia, mayor deslizamiento y menor rodamiento.
-- A menor congruencia, más rodamiento y menor deslizamiento.
1. Artrokinemática. Relación de planos en la superficie interna de la articulación. Se relaciona directamente con el rodar-deslizar.
2. Osteokinemática. Dibujo en el espacio del movimiento del hueso (como un todo). Se relaciona directamente con los planos sagital, frontal, horizontal y sus ejes correspondientes. Todos los movimientos humanos lo hacen en torno a ejes.
RELACIÓN DE PLANOS Y EJES
Veamos dos casos.
a) Primero en qué condiciones de planos se cumple la regla CC.
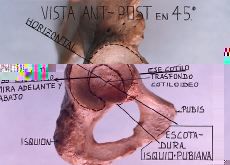
b) Si el plano convexo y su cóncavo cumplen con la condición de tener radios casi iguales; además, si las superficies de contacto entre ellas es amplia (área de la superficie de una esfera: ¼ · r
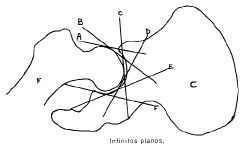
2), como es en la cadera, no tienen un plano, sino infinitos planos, como se quiera. Por tanto, la condición de movimeinto entre ellas siempre presentará un plano con eje perpendicular, lo cual anula la regla concavoconvexa. A mayor superficie de contacto entre componentes (partner) de radios de curvatura similar, menos se cumple la regla convexocóncava, porque ella exige que hayan dos planos de contacto paralelos entre sí (también paralelos al eje); en cualquier movimiento de una esfera dentro de otra, cuyas superficies están en contacto, lo hará en torno a un eje que siempre estará perpendicular a un punto del plano inmóvil de la otra esfera, lo cual producirá rotaciones de deslizamiento que se anulan en torno al eje.
c) No es lo mismo «plano de movimiento» que «plano de la superficie de contacto» (que desliza o rueda). Esta confusión nace porque se hacen sinónimos.
Para aclararlo veámoslo a través de varios ejemplos:
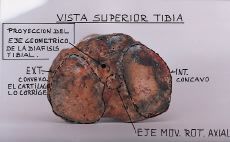
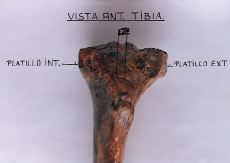
1. Rodilla. La tibia se mueve en un plano sagital y su eje es del plano frontal o, si se prefiere, transversal.
Sin embargo, las superficies articulares cotílea y tibial son perpendiculares al plano sagital y están ubicadas más o menos horizontalmente.
La regla CC se refiere al plano artrokinemático, o sea, al plano de los cóndilos y platillos tibiales y no al plano del hueso (osteokinemática).
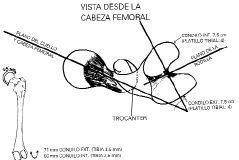
2. Cadera. La superficie del fémur (cabeza) y el cotilo tienen infinitos planos de contacto que cubren y mezclan los tres planos clásicamente conocidos: sagital, frontal y horizontal. En la flexoextensión el fémur se mueve osteokinemáticamente en el plano sagital, en tanto que en la intimidad de la cabeza femoral existen movimientos en infinitos planos, dado que la esfera está en contacto en múltiples planos que van desde el sagital hasta el frontal. Aquí no se cumple a plenitud la condición de planos que requiere la regla CC.
d) También hay que diferenciar «centro de curvatura anatómica« y «eje instantáneo de rotación». No siempre coinciden; más aún, difícilmente coinciden porque el centro de curvatura es un punto anatómico estático y el eje instantáneo es dinámico, fisiológico y depende de varios factores relacionados con el movimiento, tales como acción muscular, tensión de ligamentos, además de la mecánica de las curvaturas óseas articulares.
Artrokinemáticamente deben haber dos planos paralelos entre sí: uno rueda u/o desliza y el otro es fijo (por ejemplo, cóndilos femorales con respecto a la superficie tibial). El plano de la superficie que hace de móvil tiene un eje de movimiento paralelo al plano de la superficie no móvil. Ésta es la condición indispensable para que haya rodar-deslizar y se cumpla la regla CC (Fig. 3).
Visto osteokinemáticamente la superficie móvil se mueve en un plano sagital y el eje sigue siendo transversal-horizontal.
La superficie del hueso móvil (su cartílago) es perpendicular al plano osteokinemático. De hecho, tanto los cóndilos como los platillos tibiales no están en el plano sagital, sino horizontales y más o menos perpendiculares a él. Esto debe tenerse claro en la nomenclatura para no producir confusión: cuando se habla del plano de las superficies debe entenderse que se está observando el movimiento desde una perspectiva artrokinemática (Fig. 4).
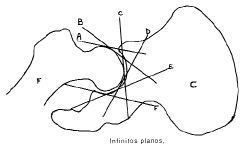
Nota. Como en la anatomía humana no hay superficies articulares totalmente planas, siempre --en rigor-- habrá varios planos, pero éstos varían poco entre sí y su eje final (sumatorio) es paralelo a la sumatoria también de planos del partner fijo. Esto basta para que se cumpla la regla CC. En la cadera los planos son tantos que algunos (en la periferia del movimiento) son fracamente perpendiculares al plano del partner fijo, lo cual hace muy difícil el pleno cumplimiento de la regla CC en varios de los movimientos (Fig. 5).
Infinitos planos perpendiculares impiden el cumplimiento de la regla CC.
Recordemos que la física nos enseña que siempre el eje de movimiento es perpendicular al plano de ese mismo movimiento.
ANÁLISIS FÍSICO PARA EL CUMPLIMIENTO DE LA REGLA CONCAVACONVEXA
Relación eje de curvatura
a) Para que se produzca deslizamiento debe haber congruencia. No basta sólo este hecho para que se cumpla la regla CC. Sólo se ha señalado una característica física para que ocurra deslizamiento. Para que ese deslizamiento lo sea según la regla CC debe concurrir otro aspecto físico esencial que veremos a continuación.
b) El deslizamiento debe ser del tipo sin eje, es decir, una superficie desliza en una sola dirección sobre la otra.
El tipo de deslizamiento con eje no permite la aplicación de la regla convexocóncava. El eje de movimiento debe ser paralelo al plano de componente óseo (partner) fijo.
MÉTODO
En primer lugar se hizo un análisis de los conceptos de física aplicables al movimiento articular. Luego se estudió el comportamiento de tales conceptos de física (expuesto en el marco teórico) en cuatro articulaciones de la anatomía humana. Se usaron modelos anatómicos con huesos humanos. El trabajo consistió básicamente en un análisis del cómo se comportaba cada movimiento de una rotación desde el punto de vista artrokinemático (rodar y deslizar).
Se eligió la articulación escapulohumeral, la humerocubital, la cadera y, finalmente, la rodilla. En cada una de ellas se analizó cada movimiento en su relación con el plano en que se efectuaba.
Se omitió la dinámica muscular involucrada en la ejecución activa de los movimientos porque ese es otro trabajo. En esta oportunidad sólo interesó saber el comportamiento de las superficies articulares en relación con la regla convexocóncava.
Se describe a continuación el análisis y conclusiones de lo investigado en cada una de las articulaciones separadamente.
HOMBRO
El hombro, con sus movimientos en tres planos, es una articulación importante de analizar en cuanto al cumplimiento de la regla convexocóncava. Observaremos que en cada plano se comporta de un modo particular (Figs. 6, 7, 8, 9, 10 y 11).
Flexoextensión (plano sagital)
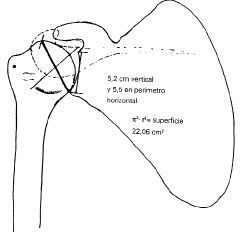
El plano de la glenoides es vertical en sentido anteroposterior, o sea, está en el plano sagital: el eje de la cabeza humeral es perpendicular al plano glenoideo; por tanto, no se cumple la condición para la regla convexocóncava (ésta tiene relación con el eje instantáneo de rotación del componente óseo móvil, el cual debe ser paralelo al plano fijo). La cabeza humeral está orientada hacia arriba-adentro atrás (rotación interna) y tiene un volumen de un tercio de esfera que alcanza a 26,17 cm
2. Esto, calculado a 2,5 cm el radio (2 rh). El perímetro es de 18,849 cm (Figs. 12 y 13).
Abducción aducción (plano frontal)
Ya dijimos que el plano de la glenoides es vertical anteroposterior, o sea, sagital. El eje instantáneo de rotación es anteroposterior; por tanto, son paralelos y se cumple la condición para que funcione la regla convexocóncava. En la ABD el movimiento del húmero (frontal) es hacia arriba y la parte de la superficie de la cabeza que hace contacto con la glenoides se dirige hacia caudal (abajo).
Según Kapandji (4) es realizada por los rotadores interno y externo que bajan la cabeza (Fig. 14).
En la abducción horizontal el eje es vertical y, por tanto, paralelo a la superficie de la glenoides. La aducción (desde el plano frontal al sagital) produce un deslizamiento posterior de la cabeza humeral y la abducción (regreso) un deslizamiento anterior. La regla CC se cumple plenamente.
Rotaciones (plano horizontal)
El plano de la glenoides es vertical anteroposterior (sagital).
El eje instantáneo de rotación es vertical; por tanto, se cumple la condición de paralelismo para la regla convexocóncava (CC).
En la rotación externa la cabeza desliza hacia adelante.
En la rotación interna la cabeza desliza hacia atrás (Fig. 15).
En la rotación, con el húmero en 90° de abducción, el eje instantáneo de rotación es horizontal y frontal (sigue la diáfisis humeral); por tanto, perpendicular al plano de la glenoides. No se cumple la regla CC.
En resumen
La regla convexocóncava (CC) no se cumple para la flexoextensión. Se cumple plenamente para la ABD y para las rotaciones.
Como la superficie efectivamente en contacto entre la glenoides y la cabeza humeral es mucho menor que en codo y cadera, es posible manejar kinésicamente estos deslizamientos fisiológicos, con tomadas adecuadas, para agregar un mayor deslizamiento terapéutico si fuera necesario.
CODO
Humerocubital
Tróclea humeral
El eje de movimiento está en la epífisis inferior del húmero, siguiendo la regla que dice que el eje está siempre en el componente convexo de la articulación.
El eje de movimiento flexoextensor es frontal-horizontal (Fig. 23). El plano de contacto del cúbito con respecto a húmero es frontal; por tanto, el eje de movimiento es paralelo a este plano, lo cual cumple la condición para la regla CC.
Sólo hay deslizamiento biomecánico y no hay rodamiento porque el radio de curvatura del cúbito (su módulo) es muy parecido al de la tróclea humeral.
Recordar que el deslizamiento está en directa proporción con la congruencia que tengan los radios de curvatura de los componentes (partner) cóncavo y convexo (Figs. 16, 17, 18, 19, 20, 21, 22, 23 y 24).
En resumen
En la flexoextensión no se puede agragar un deslizamiento artrokinemático terapéutico por la gran congruencia de sus componentes óseos (partner).
Este deslizamiento es sólo el que permite el movimiento osteokinemático del cúbito para desplazarse en el plano sagital (deslizamiento curvo).
El plano de la superficie cubital es paralelo al eje de movimiento, lo que permite cumplir la condición de paralelismo para la regla CC.
En relación a la rodadura (la regla CC dice que rueda en el mismo sentido que el movimiento del hueso), el codo no permite rodamiento por la gran congruencia de los componentes óseos. Éste, teóricamente, debería ser de atrás-adelante (si va de la extensión a la flexión).
CADERA
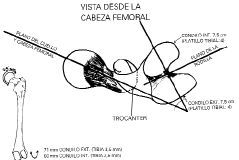
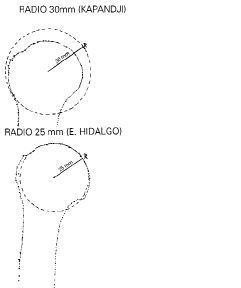
La cabeza femoral tiene un radio de 2,5 cm según Kapandji (4).
Si aceptamos esto, el cálculo matemático nos da una superficie de 33,5 a 52,3 cm
2, ya que la cabeza es de dos tercios de esfera (2 rh).
El radio anatómico de la cabeza femoral y el radio del cotilo son semejantes; por tanto, tienen gran congruencia. En esta situación se produce deslizamiento y no hay rodamiento.
Si observamos la figura 5 se aprecia que el cotilo y la cabeza, al tener dos tercios de sus respectivas superficies en contacto, presentan una disposición muy congruente. En cualquier movimiento se producen deslizamientos en variados planos, lo que dificulta su análisis (Figs. 25, 26, 27 y 28).
Plano sagital: flexión-extensión
En la flexión el eje de movimiento femoral es frontal (10° abierto hacia adelante y adentro), ya que la flexión-extensión es sagital. En el cotilo se produce un deslizamiento circular por delante de ese eje. La mitad posterior (en un corte frontal) de la cabeza desliza hacia arriba y la mitad posterior desliza hacia abajo. No se cumple la regla CC (Figs. 29, 30 y 31).
Plano frontal: abducción-aducción
El eje es anterior-posterior sagital.
En la abducción la superficie de la cabez femoral desliza hacia abajo en su relación con el cotilo; en la aducción la superficie de la cabeza desliza hacia arriba. Se cumple la regla CC.
Es importante consignar que la parte de la cabeza que está por fuera del eje anterior-posterior sagital no tiene contacto con el cotilo; por tanto, no hay roce (corresponde al cuello femoral).
Pero la gran congruencia no permite rodadura y tampoco un deslizamiento terapéutico.
Rotaciones en plano horizontal
El eje del movimiento es vertical.
En una posición bípeda en la rotación interna hay deslizamiento posterior y en la rotación externa hay deslizamiento anterior. Se cumple la regla CC.
En posición sentada el eje es horizontal y sigue la diáfisis femoral; por tanto, es paralelo al cotilo. En la rotación externa la cabeza desliza hacia arriba y en la
interna hacia abajo.
En resumen
En la ABD-AD y en las rotaciones se cumple la regla CC, no así en la flexión-extensión (plano sagital). Aun cuando en la ABD se cumple la regla CC, la movilización terapéutica en el sentido del deslizamiento no es posible porque la cabeza encaja en dos tercios de la cavidad cotiloidea y, dada la gran congruencia de sus radios de curvatura, en tal circunstancia no se puede hacer un deslizamiento adicional, sino sólo el que permite el movimiento osteokinemático del fémur al desplazarse en el plano frontal.
En la flexión-extensión el movimiento de deslizamiento es rotatorio (y perpendicular al plano sumatorio del cotilo), por lo cual es biomecánicamente imposible hacer deslizamiento terapéutico.
RODILLA
El radio de curvatura del fémur según Kapandji (4) es:
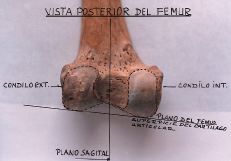
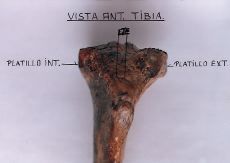
a) Interno. De atrás adelante aumenta desde 17 a 38 mm; luego desciende hasta 15 mm. En tanto el radio de curvatura del platillo tibial tiene un eje de 80 mm ubicado curiosamente por encima del cóndilo (ya que el platillo de la tibia es cóncavo) (Figs. 32, 33, 34 y 35).
b) Externo. De atrás adelante aumenta desde 16 a 60 mm y luego desciende a 12 mm.
Su contraparte presenta un platillo tibial convexo a nivel óseo y cóncavo en su menisco, con un radio de curvatura de 70 mm.
El plano anteroposterior del cóndilo externo con respecto al plano del cóndilo interno forman un ángulo de 20 a 40° hacia atrás según Kapandji (4). Personalmente he medido 30°. Luego los cóndilos no son paralelos (Figs. 36, 37 y 38).
El radio de curvatura de los cóndilos es muy diferente del radio de curvatura de las glenoides (platillos) tibiales, lo cual hace a estos radios de curvatura muy incongruentes. Su consecuencia artrokinemática es que necesariamente debe haber rodamiento y deslizamiento (Fig. 39).
El rodar-deslizar se produce del siguiente modo, según Kapandji (4), en el plano sagital:
-- Cóndilo interno. Sólo rueda los primeros 10-15° (5 a 6 mm); después rueda y desliza. Al final sólo desliza.
-- Cóndilo externo. Sólo rueda los primeros 20° (10 a 12 mm); después rueda y desliza. Al final sólo desliza.
El eje de rotación del componente óseo (convexo) condíleo es paralelo al plano de deslizamiento y rodadura; por tanto, se presenta la condición (Fig. 40).
La articulación de la rodilla es una típica articulación donde se cumple plenamente la regla CC. Además es una de las mejor estudiadas en este sentido. El eje instantáneo de rotación es paralelo al plano de las superficies en contacto (platillos y cóndilos), condición importante para permitir el cumplimiento de la regla CC. Además está facilitada por su condición de gran incongruencia, ya que el radio de curvatura de los platillos va de 70 a 80 mm, en tanto que en los cóndilos, siendo muy variable, siempre es muy por debajo de la media tibial. Ello las hace incongruentes; por tanto, el rodar-deslizar se efectúa combinado.
El platillo interior y exterior tiene entre 3,5 y 4 cm de largo anterior-posterior y los cóndilos tienen de 7 a 7,5 cm de longitud anterior-posterior, de los cuales más de la mitad son para el contacto flexoextensor femorotibial. Ello obliga a rodar y deslizar combinadamente, porque con sólo la rodadura las superficies en contacto (partner) tenderán a la luxación; al faltarle espacio el deslizamiento lo impide.
Resumen
Se cumple plenamente la regla CC. En la flexión (fémur fijo) los platillos tibiales deslizan hacia posterior; en la extensión deslizan hacia anterior.
CONCLUSIONES
El kinesiólogo (fisioterapeuta) al hacer terapia manual debe conocer la dirección normal de los deslizamientos que se producen en la intimidad intraarticular. En este trabajo se estudiaron primero los conceptos de la física aplicables a la biomecánica articular. Ello nos permitió crear un criterio en relación con las condiciones necesarias para que se cumpla la regla CC.
Estos criterios son el paralelismo del eje instantáneo de movimiento en el plano de la superficie del componente óseo fijo como, asimismo, el grado de incongruencia entre los radios de curvatura. Su posterior aplicación a cuatro articulaciones tipo del aparato locomotor nos permitió entrenarnos en el análisis para permitirnos después una aplicación al resto de las articulaciones.
La regla CC es muy importante al hacer la terapia manual, ya que la restauración del deslizamiento es clave para conseguir la recuperación de la movilidad normal y, obviamente, debemos saber primero hacia qué dirección está restringido dicho deslizamiento, respuesta que encontramos en la regla CC.
El punto central de esta investigación radica en el análisis y deducción de la fisilogía articular, aplicable a la Kinesiología.
AGRADECIMIENTO
A María Isabel Gómez Lillo, kinesióloga y profesora de técnicas kinésicas de evaluación de la Universidad de Chile.
16
| Figura 1. Deslizamiento paralelo, sin eje. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
17
| Figura 2. Deslizamiento con eje perpendicular al plano. A la izquierda se mueve de A a B; a derecha, al revés. |
18
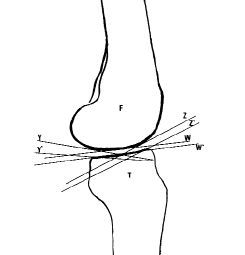
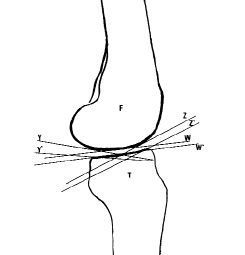
| Figura 4. El plano sagital es anterior-posterior y las superficies de tibia y fémur son casi horizontales, o sea, perpendiculares. |
| Figura 3. Las superficies en contacto son más o menos paralelas entre tibia y fémur. Los planos van cambiando de dirección debido a que las superficies son curvas, pero en cada punto mantienen su paralelismo. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
19Infinitos planos,
perpendiculares
| Figura 5. En cadera hay infinitos planos en las tres dimensiones, unos perpendiculares a otros (A-C); también paralelos (A-F). |
| El plano de tratamiento cambia en cada punto en las tres dimensiones. |
20
| Figura 8. Ejes de la glenoides. Esta superficie pequeña es aumentada (poco) por el rodete glenoideo para mejorar la congruencia con la cabeza humeral. |
| Figura 6. La superficie del húmero es mucho mayor que la de la glenoides. |
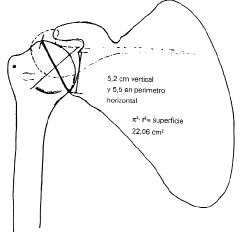
| Figura 7. Radio de curvatura y eje de rotación anatómica. |
| Se observa el radio del húmero, que en nuestro país tiene un largo de 2,5 cm [Kapandji (4) dice 3 cm]. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
Perímetro (2¼r) da
188,49 mm. La cabeza es de 1/3 de circunferencia, por tanto el perímetro es sólo 62,83 mm.
21Su perímetro es de
157,0 mm. Como la cabeza es de 1/3 de circunferencia, el perímetro real de la
cabeza es de 52,3 mm.
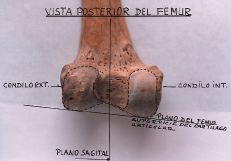
| Figura 11. Vista posterior. |
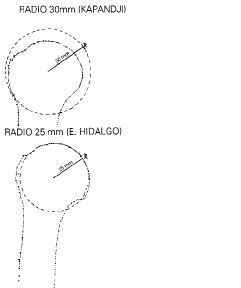
| Figura 9. Diferencias de medición del radio según Kapandji y las hechas por el autor en Chile. |
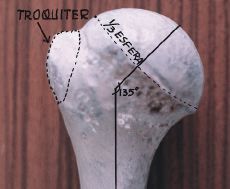
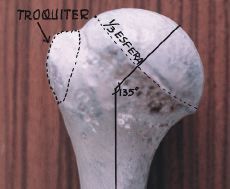
| Figura 10. Vista posterior. Ángulo de inclinación de 135°. Con plano frontal, el eje del cuello anatómico forma ángulo de 30° (declinación). |
| Figura 12. El eje de rotación del húmero se desplaza en un área. Además es perpendicular a la superficie de la glenoides. Hay deslizamiento rotatorio. |
22
| Figura 15. Rotaciones: zona en la que se mueve el eje vertical de rotación. En la rotación el eje instantáneo de rotación del húmero es vertical, o sea, paralelo a la glenoides, que en el plano sagital también es vertical, luego se cumple la condición de paralelismo: en la rotación externa la superficie del húmero desliza hacia adelante y en la rotación interna desliza hacia atrás. En la figura se hizo un corte frontal y se desplazó dicho corte hacia arriba. |
| Se observa claramente que el plano de la glenoides no es totalmente vertical. También se observa que el eje instantáneo |
| de rotación del húmero no es fijo y se desplaza en una zona. |
| Figura 13. Zona en la que se desplaza el eje instantáneo de rotación en la flexión-extensión del húmero. Hay deslizamiento rotatorio. Por detrás del eje el húmero desliza hacia abajo; por delante del eje desliza hacia arriba. |
| Figura 14. En la abducción-aducción el eje instantáneo de rotación del húmero es paralelo al plano de la glenoides; por tanto, el deslizamiento de la superficie del húmero se hace hacia abajo en la abducción y hacia arriba en la aducción, cumpliéndose plenamente la regla convexocóncava. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
CÚBITO
VISTA ANTERIOR
23
| Figura 16. Anatomía del codo. |
| Figura 17. La tróclea cubital. |
24
| Figura 20. La tróclea está abierta en 45° hacia adelante y arriba. |
| Figura 18. Plano de la cúpula radial. |
| Figura 21. Vista desde arriba de la tróclea. R-C superior: articulación radiocubital superior. |
| Figura 19. Radio de curvatura de la tróclea cubital. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
25
| Figura 22. El radio de curvatura anatómica del húmero y el del cúbito son similares; por tanto, hay mucho deslizamiento y casi nada de rodamiento. Ello no permite el cumplimiento de la regla convexocóncava en su variante de rodadura. |
| Figura 24. El eje instantáneo de rotación en la flexión-extensión varía de ángulo con respecto a la horizontal; por tanto, la excursión del antebrazo no sigue el mismo plano: a veces coincide con el plano del húmero; en otras personas cae por fuera o por dentro del plano humeral (al hacer una flexión máxima). |
| Figura 25. Corte horizontal de pelvis y epífisis femoral. |
| Se observa la gran congruencia de los respectivos ejes anatómicos de curvatura. |
| Figura 23. Ejes de curvatura del cúbito y húmero. |
26
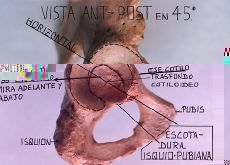
| Figura 28. Vista de frente al fondo del cotilo en un ángulo |
| de 45° hacia atrás y arriba (porque el cotilo mira hacia adelante y abajo). |
| Figura 26. El cotilo pelviano tiene una angulación entre 30 y 40° hacia adelante y abajo para recibir la cabeza femoral. |
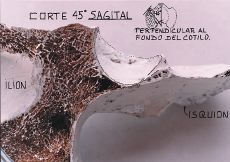
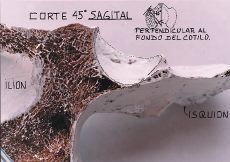
| Figura 27. Corte a 45° del plano sagital. Se observa que el cotilo es casi una mitad de esfera y el rodete cotiloideo aumenta bastante la superficie de contacto con la cabeza (un 16% más). |
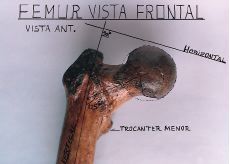
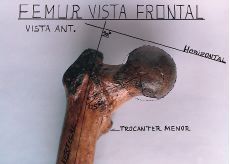
| Figura 29. Fémur: vista superior y ángulo de declinación. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
27
| Figura 30. Fémur: corte semifrontal y su radio de curvatura. |
| Figura 31. El eje del cuello tiene un ángulo de 125° de inclinación con respecto al eje diafisiario. Además se ve el radio y circunferencia de la cabeza femoral. |
28
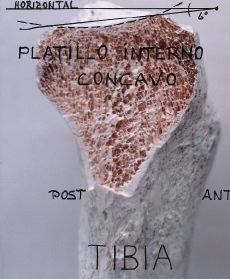
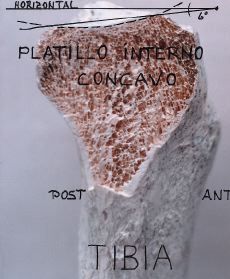
| Figura 32. Corte sagital de tibia. La tibia en su platillo interno es cóncavo hacia arriba. |
| Figura 33. Corte sagital del fémur. El cóndilo interno tiene radios de curvatura variable, aumentando desde atrás hacia adelante. |
| Se observa la zona de contacto femorotibial en parte posterior y femoropatelar por delante. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
29
| Figura 34. Corte sagital de tibia. El platillo externo es cóncavo y la concavidad será dada por el cartílago bicóncavo. |
| Figura 35. Corte sagital del fémur. Radios de curvatura variables. |
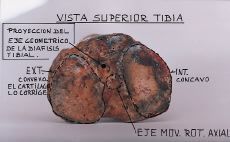
| Figura 36. Eje vertical de la rotación axial. Por delante y afuera está el eje (proyección) de la diáfisis tibial. |
30
| Figura 37. En visión frontal se ve la zona en la que se desplaza el eje instantáneo de rotación para los movimientos de rotación femorotibial. |
Zona de contacto de la articulación femoropatelar (por delante) y zona de contacto femorotibial (por detrás).Radios de curvatura (Kapandji)
Cóndilo interno: de 17 * 38 * 15 (ant.)
Cóndilo externo: 12 (post) * 60 (punto) * 16 (ant.)
Glenoides interno: 80 mm con eje muy encima del cóndilo (glenoides cóncava).
Glenoides externo: 70 mm con eje muy por debajo de platillo tibial porque la glenoides es convexa.
| Figura 39. El radio de curvatura anatómico de la tibia es mucho mayor que el del fémur; por tanto, son muy incongruentes, lo que permite un rodamiento y deslizamiento combinados. En la figura sólo se dibujaron dos ejes como ejemplos. |
| Figura 38. Vista desde abajo hacia arriba del fémur. El plano del cuello es distinto del plano de los cóndilos. Constante de crecimiento: si la superficie femoral tiene 75 mm de largo y la tibial 40, la constante «K» es 1.875 y son directamente proporcionales: A= K * B. A: Longitud del fémur. B: Longitud de la tibia. K: Constante de crecimiento. |
| Figura 40. Desde vista anterior. Corte frontal del fémur. Se observa el eje intercondíleo. |
REVISTA IBEROAMERICANA DE FISIOTERAPIA
Y KINESIOLOGÍA
Volumen 1
Número 1
Enero-Marzo 1998
31BIBLIOGRAFÍA
sson (5).