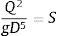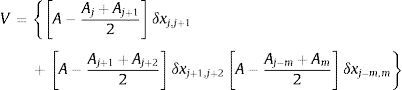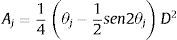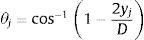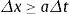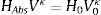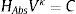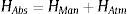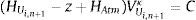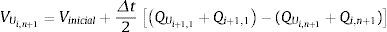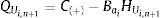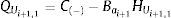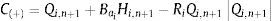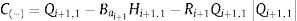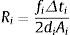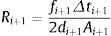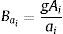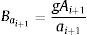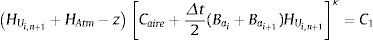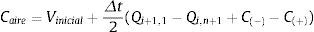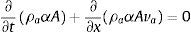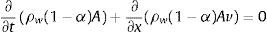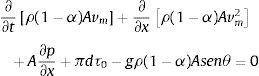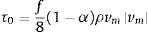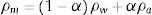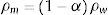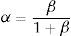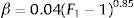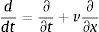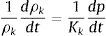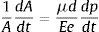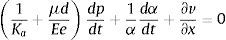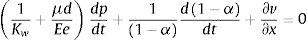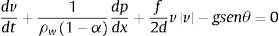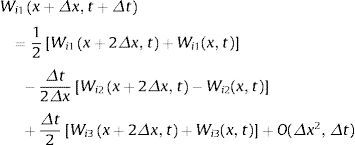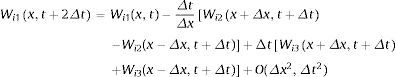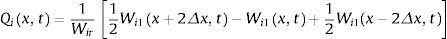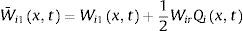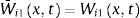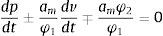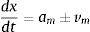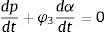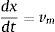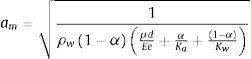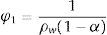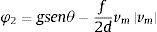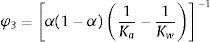En este artículo se presenta el análisis de los efectos perjudiciales y benéficos del aire atrapado en transitorios hidráulicos en conductos a presión, cuando existe aire atrapado en forma de bolsas de aire con y sin una mezcla homogénea de agua-aire generada por un salto hidráulico en el extremo aguas abajo de las bolsas. Para este fin, se sigue una metodología para identificar la posible ubicación de las bolsas de aire, posteriormente se cuantifica su volumen y el porcentaje de aire en la mezcla, para finalmente evaluar los transitorios con un modelo numérico implementado con base en los métodos de las características y de Lax-Wendroff. El procedimiento presentado se aplica a un caso de estudio de un acueducto a bombeo o impulsión para validar la metodología propuesta. Los resultados muestran que las bolsas de aire pequeñas causan un incremento importante de las presiones máximas a todo lo largo del perfil de la conducción, por otra parte los transitorios hidráulicos reducen significativamente su valor, al incrementar el volumen de aire y el porcentaje de aire en la mezcla homogénea.
This paper presents an analysis of the potential effects on pressure transients of air entrained at the downstream end of entrapped air pockets followed by a hydraulic jump in pressurized pipelines. For this purpose, a methodology is followed to identify the potential locations, where air pockets can be found along the pipeline, to compute the air-void fraction downstream of the air pockets and the volume of the pockets, respectively. Further, the calculations were carried out using a numerical model based on the methods of characteristics and the Lax-Wendroff. A case study of an existing pumping system was considered to validate the methodology proposed. The results show that small air pockets cause an important enhancement of the maximum pressures throughout the pipeline profile, conversely pressure transients are significantly reduced with increasing air-pocket volumes and bubbly flow air content.
La presencia de bolsas de aire atrapadas en conductos a presión puede reducir de forma importante el transporte de agua en este tipo de sistemas. En acueductos a bombeo o impulsiones, la presencia de aire se puede reflejar en un incremento en el consumo de energía eléctrica y la reducción del caudal. Estos problemas siguen ocurriendo hoy en día, incluso en acueductos construidos recientemente, debido a la falta de criterios de diseño que hagan que éstos funcionen eficientemente.
En los acueductos a bombeo el análisis de los transitorios hidráulicos se hace generalmente asumiendo que no hay aire atrapado en los mismos. Sin embargo, en muchos de estos sistemas el aire puede ser introducido a través de los sellos defectuosos de las juntas y las válvulas, cuando se presenta una presión menor a la atmosférica en la tubería. Además, es bien sabido que el agua contiene aproximadamente un 2% de aire disuelto, si la presión baja o la temperatura del agua aumenta el aire escapa de la solución y forma pequeñas bolsas de aire, que pueden migrar a los puntos altos o intermedios de la tubería y unirse al aire que pudo haber quedado acumulado por un mal purgado de la conducción. Asimismo, las bombas pueden introducir entre un 5% y 10% de aire por volumen de agua mediante los vórtices que se forman en la succión de éstas [1].
Varios investigadores han demostrado que la presencia de bolsas de aire en acueductos puede incrementar de forma importante las presiones máximas durante un transitorio hidráulico, lo suficiente para causar la falla de la tubería. La magnitud del daño dependerá de la cantidad y del lugar donde se encuentre localizado el aire no disuelto, de la configuración de la conducción, así como de las causas que generan el transitorio. Por ejemplo, se ha demostrado que las bolsas de aire pequeñas pueden incrementar considerablemente las presiones transitorias, lo suficiente para causar la rotura de tuberías [2–9]. Por el contrario, la formación de grandes bolsas de aire en los acueductos puede ayudar a reducir el valor de las sobrepresiones causadas por la ocurrencia de transitorios hidráulicos [10–13].
La explicación física del porqué las bolsas pequeñas generan elevadas sobrepresiones, por un lado se debe a la baja densidad del aire, es decir a su baja inercia que lo hace fácil de comprimir. Por el contrario, cuando las bolsas de aire son grandes, éstas actúan como un colchón de aire o amortiguador el cual ayuda a reducir las presiones transitorias. Gahan [14] después de realizar una revisión extensiva y detallada de las investigaciones relativas a los transitorios hidráulicos con aire atrapado resalta, que el criterio que establece si una bolsa de aire es pequeña o grande dependerá de su efecto en los transitorios.
Un ejemplo de una bolsa de aire pequeña es presentado en Koelle [15], el autor describe un accidente ocurrido en una estación de bombeo. Después de un análisis teórico concluye, que existe un volumen crítico de aire (bolsa de aire pequeña) que genera un pico de presión máximo, los resultados también revelaron que al aumentar el volumen de la bolsa el pico de presión se reduce. Este volumen crítico también fue detectado entre otros por Nakamura y Tomita [16].
En el mismo sentido, al estar el aire distribuido homogéneamente en forma de pequeñas burbujas su efecto será más difícil de predecir. Uno de los efectos más notables es una importante disminución de la celeridad, incluso con una pequeña cantidad de aire. La presencia de una mezcla homogénea de agua-aire fluyendo por un conducto a presión produce una reducción de las presiones transitorias, debido a la reflexión interna de las ondas de presión en la mezcla [17]. Sin embargo, también se ha encontrado que las presiones transitorias varían con el porcentaje de aire contenido en la mezcla, y en algunas ocasiones estas presiones son mayores a las obtenidas sin considerar aire en la conducción. Se dice que este efecto se debe al proceso de expansión y compresión de las burbujas de aire [18].
En este artículo se presenta una metodología para evaluar el efecto en transitorios hidráulicos de las bolsas de aire con una mezcla homogénea de agua-aire en el extremo final de las bolsas. Las bolsas de aire que se podrían acumular en los puntos altos e intermedios de los conductos a presión, se localizan mediante una metodología que ha sido probada con éxito en sistemas que actualmente operan adecuadamente [19]. De la misma manera, la teoría del flujo gradualmente variado es utilizada para obtener los perfiles de flujo bajo las bolsas de aire y las variables necesarias para obtener el volumen de aire contenido en las mismas [9]. Además, la expresión propuesta por Ahmed et al.[20] es utilizada para conocer la relación agua-aire en la mezcla introducida por un salto hidráulico. Finalmente, al conocer la ubicación de las bolsas de aire y su volumen y el porcentaje de aire en la mezcla, se realiza la simulación de los transitorios con un modelo numérico basado en los métodos de las características y de Lax-Wendroff [21].
2Aire en conductos a presión2.1Bolsas de aireEl aire atrapado en los conductos a presión puede migrar a sus puntos altos, donde no hay válvulas de aire o ventosas instaladas y formar bolsas de aire que pueden quedar estacionarías, cuando la fuerza de arrastre del flujo no es capaz de vencer la fuerza de flotación de las bolsas. En el mismo sentido, si la línea de piezométrica corta la tubería en las cimas de la conducción donde hay ventosas colocadas, el aire se va a introducir y formará bolsas de aire que estarán a presión atmosférica y el flujo debajo de éstas será a superficie libre [9,22–24].
Si una bolsa de aire se extiende hacia aguas abajo de una tubería con pendiente descendente, el tirante crítico o calado crítico puede ser mayor que el tirante en el extremo final de la bolsa, por lo tanto se va a presentar un salto hidráulico que introducirá aire en forma de pequeñas burbujas, que pueden aglutinarse y formar burbujas más grandes y pequeñas bolsas de aire, formando una mezcla de agua-aire [9].
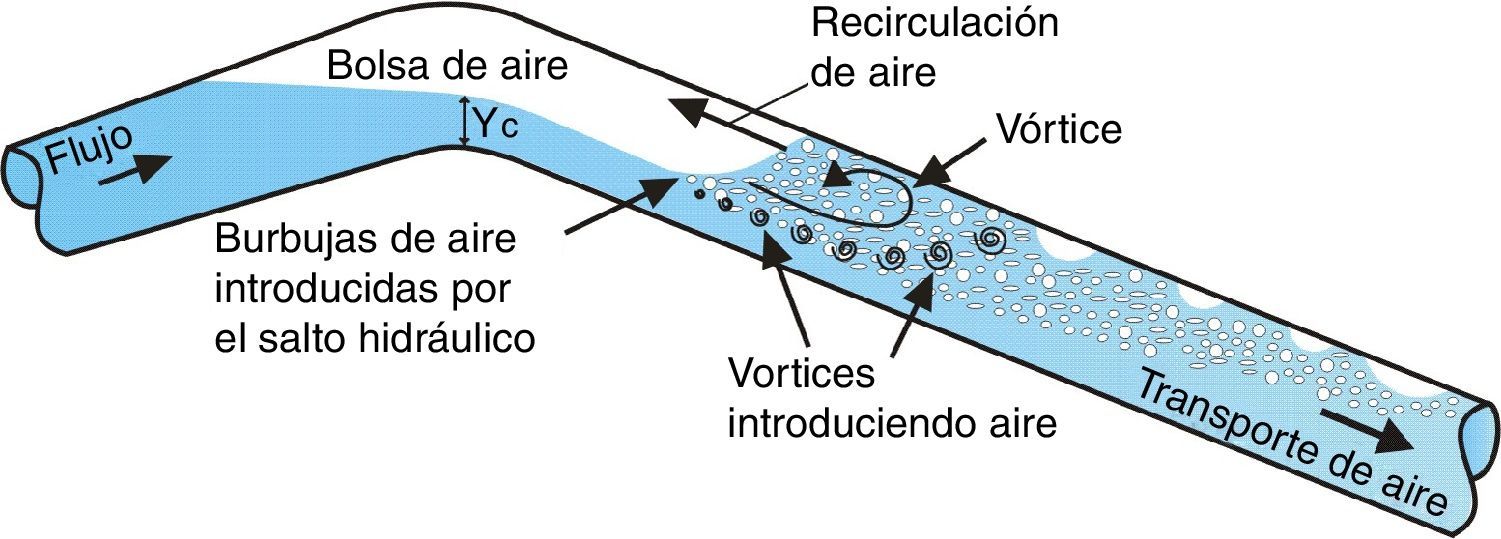
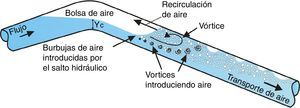
2.2Entrada de aire a través de un salto hidráulicoLa transición de flujo a superficie libre a flujo presurizado en tubos con pendiente descendente ocurre generalmente mediante un salto hidráulico, que debido a su acción turbulenta introduce aire hacia aguas abajo del conducto. Al ser transportado el aire hacia aguas abajo por el flujo de agua, las pequeñas burbujas de aire pueden unirse y formar burbujas de mayor tamaño y pequeñas bolsas de aire. Dependiendo del caudal de agua y de la pendiente de la tubería, el aire avanzará o regresará a contra flujo a través del salto (fig. 1).
Kalinske y Robertson [25] y Walski et al.[22] observaron durante sus experimentos, que la transición de tubo parcialmente lleno a tubo lleno depende de la pendiente descendente. Cuando la pendiente es moderada ocurre una transición suave, mientras que cuando la tubería tiene una pendiente descendente pronunciada al final de la bolsa de aire ocurre un salto hidráulico que sella el conducto.
Wisner et al.[26] describieron que la remoción de grandes bolsas de aire en tuberías puede ocurrir de las siguientes maneras: 1) Generación y entrada y 2) Arrastre. Generación se refiere a la formación de burbujas de aire, debido a la acción turbulenta del salto hidráulico que se presenta en el extremo aguas abajo de la bolsa de aire; el término entrada se utiliza para describir el movimiento de las burbujas de aire generadas por el salto e introducidas hacia la tubería que fluye completamente llena de agua. Arrastre, es la expresión que indica la remoción completa de las burbujas de aire introducidas por el salto hidráulico, para lo cual el agua en el conducto debe tener una velocidad mínima para iniciar el transporte del aire.
Los trabajos más destacados en cuanto a la cantidad del aire introducido por un salto hidráulico en conductos cerrados son los de Kalinske y Robertson [25], Wisner et al.[26], U.S. Army Corps of Engineers [27], Ahmed et al.[20] y más recientemente Escarameia [28].
2.3Transporte de aire en tuberíasHasta ahora la discusión se ha enfocado en el proceso de entrada de aire mediante un salto hidráulico a una tubería. Por otra parte, igual de importante es el proceso de transporte del aire en un conducto que fluye completamente lleno de agua. Cuando el aire se encuentra en la zona a tubo lleno, pueden presentarse dos fenómenos, que el aire regrese a contra flujo o que sea transportado hacia aguas abajo, tal como se muestra en la fig. 1.
Investigaciones teóricas y experimentales se han realizado para estudiar la habilidad de los vórtices para atrapar burbujas de aire en sus núcleos e impulsarlas una distancia considerable, hacia aguas abajo del punto de entrada. Las principales fuerzas que actúan sobre las burbujas de aire son las fuerzas de arrastre y de flotación [29].
Ervine [29] comenta que la cantidad de aire transportado en tuberías con pendientes descendentes no sólo depende de la cantidad de aire introducida, sino también de las condiciones aguas abajo del punto de entrada y de la pendiente de la tubería. Si las condiciones de flujo son capaces de remover las burbujas, es decir, la velocidad del flujo es mayor a la velocidad de remoción, entonces el parámetro más importante que afecta el arrastre o el transporte de aire hacia aguas abajo es la relación entre la longitud y el diámetro del conducto (L/D) aguas abajo del punto de entrada de aire. Existen por lo menos tres diferentes relaciones de L/D que afectan el transporte de aire. Por ejemplo, cuando L/D<5 el aire introducido en el punto de entrada es transportado hacia aguas abajo y removido por completo del tubo. Para una relación 5<L/D<20 las burbujas de aire van a elevarse hacia el techo de la tubería debido a su fuerza de flotación, asimismo, estas burbujas van a unirse entre sí para formar pequeñas bolsas de aire, que se van a mover pegadas a la clave del tubo. En este caso el régimen de flujo que se presenta es el de una mezcla de agua con burbujas y pequeñas bolsas de aire que pueden llegar a ser expulsadas de la tubería. Finalmente, para L/D>20 las burbujas de aire se unen y forman bolsas de aire que se adhieren al techo de la conducción, las cuales sólo podrán ser removidas si el flujo tiene la capacidad de transportarlas. Cuando las bolsas de aire se hacen más grandes, su velocidad disminuye y su fuerza de flotación aumenta, hasta llegar a un punto donde las bolsas regresan a contra flujo a través del salto hidráulico para volver a formar parte de la bolsa de aire estacionaria.
El caso ideal sería que las burbujas y bolsas de aire fuesen removidas de la conducción por el flujo de agua. Por tanto, varios investigadores han analizado el movimiento del aire en conductos a presión, enfocándose principalmente en la velocidad de remoción también llamada velocidad crítica, es decir la velocidad mínima del agua necesaria para expulsar el aire de la conducción. Para tal fin, algunos utilizaron burbujas estacionarias en un tubo con flujo a tubo lleno [30,31], mientras que otros analizaron el movimiento de burbujas en tubos llenos de agua estática [32,33].
Recientemente, Escarameia [28] propuso una ecuación para evaluar la velocidad de remoción del aire en pendientes descendentes suaves (0° a 22.5°). En el mismo sentido Pothof y Clemens [34] realizaron una investigación en siete dispositivos experimentales, para encontrar la velocidad necesaria para evitar la acumulación de aire en tuberías con pendientes descendentes.
Por todo lo antes mencionado, sin duda son varias las expresiones analíticas que se pueden utilizar para evaluar la velocidad de remoción para expulsar el aire de un conducto a presión. Por tanto, el uso de cuál sea la ecuación elegida para el diseño o análisis de este tipo de sistemas debe ser utilizada con cautela y juicio ingenieril, porque ésta podría no ser aplicable para diseñar o estudiar una determinada conducción.
En este trabajo se utiliza la expresión analítica (ec. 1) propuesta por Pozos et al.[19], para estudiar el comportamiento de las burbujas y bolsas de aire en tuberías con pendientes descendentes. La efectividad de dicha ecuación ha sido validada con investigación teórico-experimental, así como con el análisis de conducciones en campo. La ecuación fue obtenida al realizar el balance de la fuerza de arrastre y la componente de la fuerza de flotación en sentido contrario al flujo, actuando sobre una burbuja de aire estacionaria en una tubería fluyendo completamente llena. La comparación de los resultados experimentales con las predicciones obtenidas utilizando la ecuación (1) mostró muy buena coincidencia. Esta expresión se puede utilizar para analizar conductos a presión en la etapa de diseño, así como en aquellos que se encuentran en operación. La mencionada expresión puede escribirse como:
donde Q es el caudal de agua que circula por la tubería (m3/s), D es el diámetro del tubo (m), g es la aceleración de la gravedad (g=9.81m/s2) y S es la pendiente de la tubería. El término del lado izquierdo de la ecuación (1) se conoce como parámetro de gasto adimensional (PGA).El análisis dimensional realizado por Wisner et al.[26] indica que la velocidad del flujo que remueve las burbujas de aire y las bolsas, depende principalmente de D, g y S. Por lo tanto, después de un desarrollo matemático la ecuación (1) se representa de esta forma, además al ser el caudal una variable conocida desde el diseño del acueducto, entonces se optó por utilizar dicha variable en lugar de la velocidad del flujo de agua. Para una descripción completa del desarrollo de la ecuación (1) el lector debe remitirse a Pozos et al.[19].
Para establecer si las bolsas de aire podrían permanecer estacionarias en algunos puntos altos de un conducto a presión, el PGA debe ser calculado para el rango de gastos con los que opera el sistema y comparado con todas las pendientes de la tubería que componen la conducción. Cuando PGA>S las burbujas y bolsas de aire serán removidas por el flujo de agua. En caso contrario, si PGA<S el aire regresará en sentido contrario al flujo y una bolsa de aire se podría acumular y quedar atrapada en la conducción.
La ecuación (1) se utilizará más adelante para analizar la posible acumulación de bolsas de aire en los puntos altos de la conducción del caso de estudio.
3Volumen de las bolsas de aireDebido a que en la literatura no se reporta ninguna metodología para evaluar el volumen de las bolsas de aire que se acumulan en los puntos altos de los conductos a presión, Pozos [9] realizó una investigación teórica-experimental con el fin de obtener una expresión analítica (ecuación [2]) para calcular el volumen de aire en las bolsas que podrían quedar atrapadas a lo largo de una conducción.
El autor explica que el flujo debajo de las bolsas de aire puede ser considerado análogo al flujo en un canal abierto. La presión sobre la superficie de un canal abierto es la atmosférica, por otra parte la presión sobre la superficie de la bolsa de aire, aunque no atmosférica, es constante a lo largo de la misma. Por tanto, se concluyó que la teoría del flujo gradualmente variado (FGV) se puede utilizar para calcular los perfiles de flujo debajo de las bolsas.
Los volúmenes de aire contenidos en las bolsas se calcularon mediante una relación que ocupa algunas de las variables obtenidas al aplicar el Método del Paso Directo, ampliamente descrito en los libros de hidráulica de canales [35,36]. La ecuación propuesta para determinar el volumen de aire contenido en una bolsa es la siguiente:
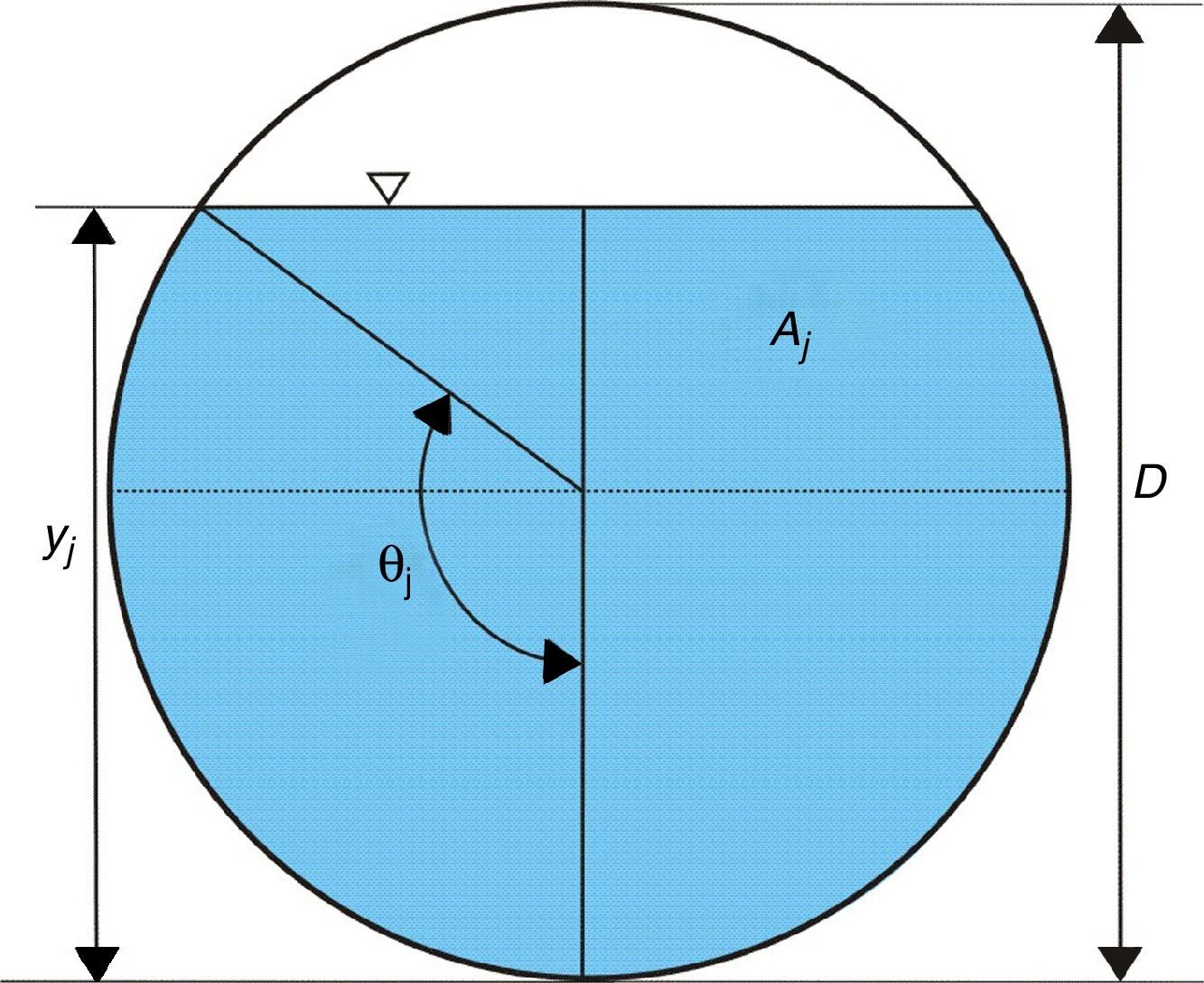
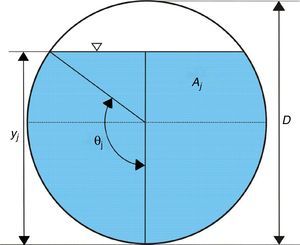
donde V es el volumen de aire en la bolsa de aire (m3), A es la sección transversal del tubo (m2), Aj, Aj+1, …, Am son las áreas de la sección transversal del flujo de agua en secciones específicas a lo largo de la tubería (m2), y δxj,j+1, δxj+1,j+2,…, δxj-m,m denotan las longitudes de los tramos en los que fue dividido el conducto (m).Para calcular las áreas hidráulicas Aj, Aj+1,…, Am, se utiliza la ecuación (3)
donde θj se define como:siendo yj el tirante o calado (m) en la sección j.En la figura 2 se muestran de forma esquemática las variables expresadas en las ecuaciones (3) y (4).
La ecuación (2) es útil para evaluar cuantitativamente los volúmenes de las bolsas de aire cuando el flujo es establecido. Por otro lado, los acueductos operan comúnmente con presiones mayores que la atmosférica, que comprimen el aire en las bolsas. En tal caso, esta expresión podría sobreestimar el volumen de aire. Es importante mencionar que, es difícil estimar de forma exacta el volumen de las bolsas de aire, porque la cantidad de aire acumulado en las tuberías es desconocida y no se puede observar. Por consiguiente, esta ecuación es adecuada para aproximar el volumen de las bolsas de aire estacionarias, debido a que ésta utiliza variables hidráulicas y se basa en una exhaustiva investigación experimental.
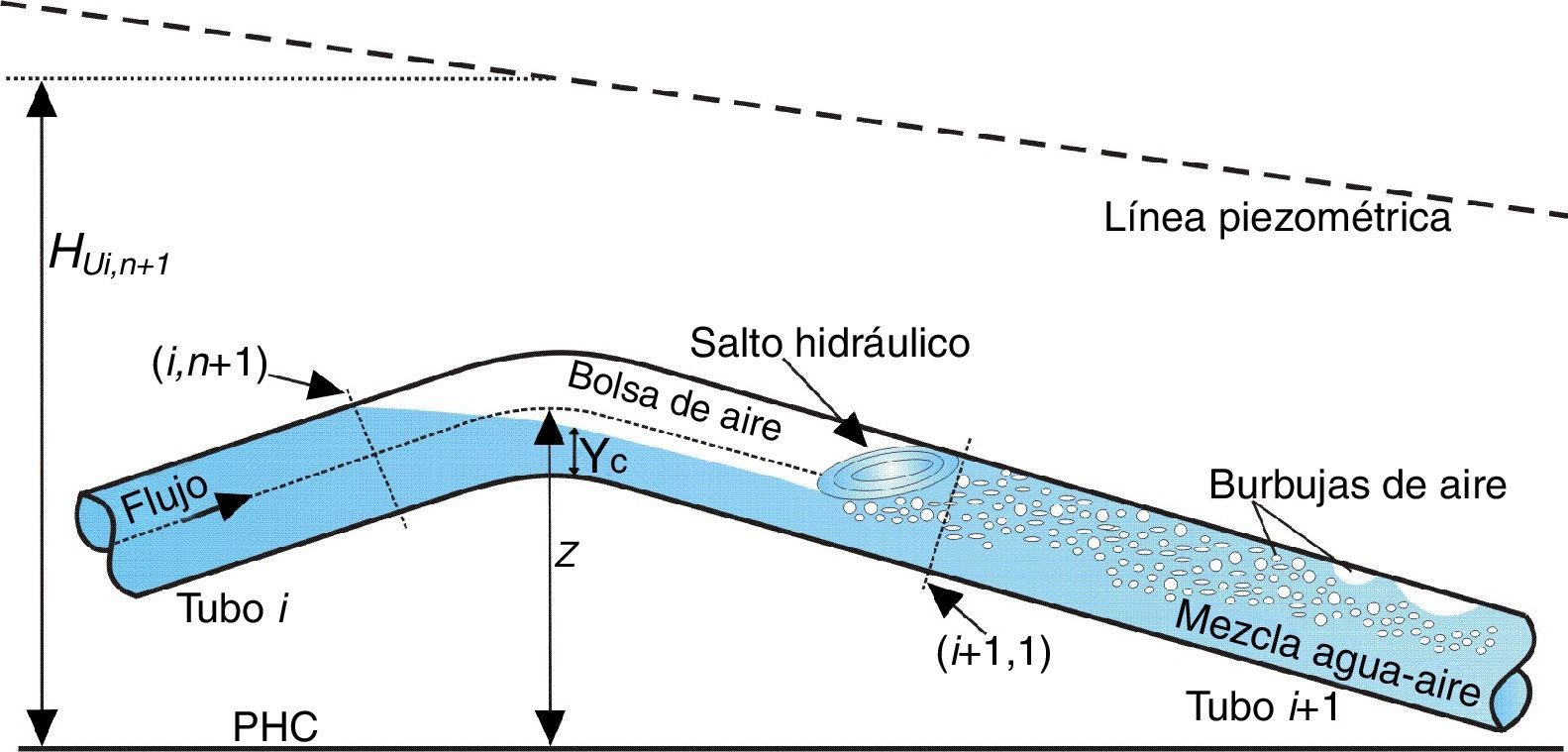
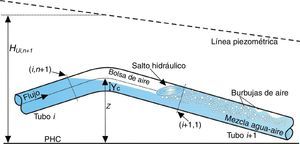
4Modelo numéricoLa influencia del aire atrapado en transitorios hidráulicos en los conductos a presión, generalmente no se considera, ni en la etapa de diseño, ni en la investigación de una falla en una conducción. Debido al indudable interés práctico del conocimiento físico del problema y a la posibilidad de evaluar los efectos benéficos o destructivos que pueden generarse, en este artículo se estudia el efecto combinado de bolsas de aire y una mezcla homogénea de agua-aire en transitorios hidráulicos en un acueducto a bombeo o impulsión. Se considera que un salto hidráulico que se ubica en el extremo final de las bolsas introduce las burbujas de aire que forman la mezcla (ver fig. 3).
El análisis del efecto de las bolsas de aire en transitorios se simula en base a la teoría y procedimientos presentados por Wylie y Streeter [37], Chaudhry [38] y Wylie et al.[39]. Las principales consideraciones adoptadas para la implementación del modelo numérico son las siguientes:
- •
El método estándar de las características es utilizado para obtener las ecuaciones diferenciales ordinarias. Posteriormente, éstas son evaluadas a lo largo de las líneas características con una aproximación de primer orden y sin interpolación para eliminar la inestabilidad numérica. Por lo tanto, la celeridad permanece constante durante el análisis.
- •
Por convenir a los cálculos, las bolsas de aire de un tamaño predeterminado se ubican en nodos coincidentes entre los tramos adyacentes de las tuberías. De esta forma se pueden obtener las presiones puntuales en los puntos donde se acumulan los volúmenes de aire.
- •
La bolsa de aire siempre permanece en su posición original durante toda la evolución del transitorio, debido a que la celeridad o velocidad de propagación de la onda de presión es más dominante que el movimiento de las bolsas. Además, las bolsas de aire nunca ocupan la totalidad de la sección transversal del tubo.
- •
Durante los cálculos el esquema de diferencias finitas se mantiene estable debido a que la condición de Courant–Friedrich–Lewy se cumple en todo momento (ec. 5)
Por otra parte, Abreu et al.[40] y Abreu et al.[41] afirman que en la mayoría de los casos de aire atrapado en acueductos, la compresión y expansión de las bolsas de aire puede simularse de mejor manera mediante un proceso adiabático reversible. Esto quiere decir que el sistema, en este caso una bolsa de aire, siempre está en equilibrio. Este fenómeno se puede representar matemáticamente como:
donde HAbs es la carga piezométrica absoluta o altura piezométrica absoluta (m) en la bolsa de aire, V es el volumen de aire en la bolsas de aire (m3), H0 es la altura piezométrica absoluta al inicio del análisis (m) y V0 es el volumen de la bolsas de aire inicial antes del transitorio (m3), y que se obtiene con la ecuación (2), κ es el coeficiente adiabático.Debido a que la ecuación (6) establece que dos estados cualesquiera de un gas ideal, que pueden unirse mediante un proceso adiabático reversible satisfacen la condición de que el producto de la altura piezométrica absoluta multiplicada por el volumen de la bolsa de aire elevado al coeficiente adiabático es igual a una constante C, la ecuación (6) puede escribirse como:
donde C es una constante que tiene las mismas unidades que el término del lado izquierdo de la ecuación (7). Por otra parte, el valor del coeficiente adiabático considerado para los cálculos aquí presentados es de κ =1.4, debido a que se considera que las bolsas de aire siguen un proceso adiabático rápido. Además, varios investigadores han demostrado numérica y experimentalmente que con el valor de κ=1.4 se predicen mejor los transitorios con aire atrapado [42–46].En el caso de la altura piezométrica absoluta, ésta se puede definir como:
siendo HMan la altura manométrica (m) y HAtm la altura de presión atmosférica (m).El modelo numérico calcula la altura piezométrica total, por lo que la altura manométrica es una variable desconocida y tendrá que ser evaluada en cada intervalo de tiempo durante la simulación del transitorio, por lo tanto la ecuación (7) también puede escribirse como:
donde HUi,n+1 es la altura manométrica sobre el eje de la tubería en la sección (i, n+1) al final del intervalo de tiempo (m), z es la distancia vertical o cota desde el plano horizontal de comparación (PHC) hacia el eje del tubo (m), y VUi,n+1 es el volumen de aire al final del intervalo de tiempo (m3). En este caso el subíndice i indica el número de tubo y el subíndice n+1 representa el segmento del i-ésimo tubo.La ecuación de continuidad para la bolsa de aire puede escribirse como:
donde Vinicial es el volumen de aire al inicio del intervalo de tiempo (m3), Δt es el incremento en el intervalo de tiempo (s), Qi,n+1 y QUi,n+1 son los caudales de agua aguas arriba de la bolsa de aire al inicio y al final del intervalo de tiempo (m3/s), respectivamente. Qi+1,1 y QUi+1,1 son los caudales de agua aguas abajo de la bolsa de aire al inicio y al final del intervalo de tiempo (m3/s), respectivamente.El subíndice U en las variables indica que éstas son desconocidas al final del intervalo de tiempo t+Δt, mientras que las variables sin el subíndice U son conocidas al inicio del intervalo de tiempo t.
Debido a que en este trabajo el método de las características es utilizado para analizar el efecto de bolsas de aire en transitorios hidráulicos, las ecuaciones de las características positiva y negativa al final de cada intervalo de tiempo se definen de la siguiente forma:
dondesiendo f el factor de fricción de Darcy–Weisbach, D es el diámetro del tubo (m), A es el área de la sección transversal del tubo (m2), g es la aceleración de la gravedad (m/s2).Si las pérdidas en la unión de los tubos no son consideradas, entonces:
Ahora se tienen cinco variables desconocidas y cinco ecuaciones, las cuales son HUi,n+1, HUi+1,1, VUi, QUi,n+1, QUi+1,1. Combinando las ecuaciones (9) y (10) y después de un desarrollo matemático se obtiene:
siendoLa ecuación (20) es no lineal y puede resolverse para HUi,n+1 mediante un método iterativo, por ejemplo el de Newton-Raphson. Los valores de las otras variables desconocidas pueden ser evaluados con las ecuaciones (9) a (19).
Asimismo, los transitorios hidráulicos con una mezcla homogénea de agua-aire en el extremo aguas abajo de las bolsas de aire, son simulados utilizando las ecuaciones del flujo homogéneo. Las ecuaciones de continuidad para el agua y el aire, así como la ecuación dinámica para la mezcla homogénea de agua-aire, conllevan a un sistema de ecuaciones diferenciales hiperbólicas que se resuelve mediante el método de Lax-Wendroff. Este esquema numérico fue elegido por sobre el método de las características, que resulta inadecuado para este tipo de flujos porque no permite una solución directa y continua de las ecuaciones en todo el dominio, es decir no es capaz de manejar complejos sistemas de discontinuidades u ondas de choque [47,48].
El modelo homogéneo aquí usado permite tratar a los dos fluidos como un pseudofluido. Se puede considerar que no hay movimiento relativo entre los dos fluidos [49,50]. Además, la compresibilidad del aire y del agua, así como la elasticidad de la tubería son incluidas en el sistema de ecuaciones.
La ecuación de continuidad para el aire se escribe como:
siendo α la concentración de aire por volumen de agua (%), ρa es la densidad del aire (kg/m3), A es la sección transversal total del tubo (m2), va es la velocidad media del aire (m/s), t es el tiempo (s) y x la distancia a lo largo de la tubería (m).La ecuación de continuidad para el agua es:
en donde ρw es la densidad del agua (kg/m3), v la velocidad media del agua, la cual se considera igual a la velocidad del aire (m/s).La ecuación dinámica de la mezcla homogénea agua-aire se presenta como:
donde p es la presión media en la sección transversal del tubo (Pa), vm=va=v es la velocidad de la mezcla (m/s), τ0 es el esfuerzo cortante en la pared del tubo (Pa) y θ es el ángulo de inclinación de la tubería con respecto a la horizontal (°).El esfuerzo cortante τ0 puede definirse en función del coeficiente de fricción de Darcy-Weisbach f:
siendo f el coeficiente de fricción de Darcy-Weisbach. Se ha demostrado que la utilización de un coeficiente de fricción para flujo estacionario, no afecta de forma significativa los resultados al ser utilizado en la simulación de flujo transitorio [51–53].La densidad de la mezcla puede escribirse como:
Debido a que la densidad del aire es muy pequeña comparada con la densidad del agua, la ecuación (26) puede expresarse como:
En el modelo numérico la concentración de aire por volumen de agua se calcula con la ecuación:
donde β es el coeficiente de aireación, que se calcula con la relación propuesta por Ahmed et al.[20], esta ecuación fue validada y está soportada en un programa de pruebas que duró tres años. Además, se realizaron un total de 2250 pruebas en conductos cerrados con variación de pendientes de 0° a 90°en donde F1 es el número de Froude al inicio del salto hidráulico.Con el propósito de formular las ecuaciones constitutivas del flujo homogéneo se utilizan las siguientes ecuaciones de transformación:
donde el subíndice k se refiere al aire (a) o al agua (w) siendo Kw y Ka los módulos de elasticidad del agua y del aire (Pa), respectivamente. E es el modulo de elasticidad de la tubería (Pa) y e es el espesor de la pared de la tubería (m), μ es el factor de restricción al movimiento de la tubería.Sustituyendo las ecuaciones (30) a (31) en las expresiones (22) a (24), además se considera que durante el transitorio no son expulsados los gases disueltos en el agua, ni ocurre variación de temperatura en los fluidos, de lo cual se obtienen las ecuaciones de continuidad para el aire y el agua, respectivamente.
Al mismo tiempo, la ecuación dinámica de la mezcla de agua-aire de forma simplificada se puede escribir de la siguiente manera:
Las tres ecuaciones antes obtenidas representan un sistema de ecuaciones diferenciales hiperbólicas no lineales, que son resueltas con el método explícito de Lax-Wendroff de dos pasos de orden dos. El primer paso en la solución se obtienen mediante el método de Lax [54] de la siguiente forma:
La aproximación en diferencias finitas del segundo paso se puede escribir como:
siendo el subíndice i=1, 2, 3, asimismo los parámetros Wi1, Wi2 y Wi3 están en función de la presión p de la tubería, de la velocidad de la mezcla de agua-aire vm, y de la concentración de aire por volumen de agua α. Los valores de los parámetros para t=t+2Δt son determinados en el instante anterior t al resolver las ecuaciones 36 y 37. Además, la estabilidad de Courant-Friedrichs-Lewy se satisface en todo momento.Es importante mencionar que cuando se utiliza el método de Lax-Wendroff para simular transitorios hidráulicos con una mezcla homogénea de agua-aire, las discontinuidades como por ejemplo las onda de choque pueden producir la amplificación del frente de onda lo que produce oscilaciones durante la simulación numérica, las cuales pueden ser atenuadas utilizando el método del suavizador de Shuman [55–57]. Este método es utilizado en el modelo numérico para atenuar las oscilaciones numéricas provocadas por las ondas de choque que se puedan presentar. El suavizador de Shuman W¯i1(x,t) se puede definir de la siguiente forma:
donde Wir es un parámetro que está en el rango del valor de Wi1(x, t). Si Qi(x, t) excede un valor de referencia Qr(x, t), es decir, Qi(x,t)>Qr(x,t) el valor del suavizador W¯i1(x,t) del parámetro Wi1(x, t) se obtiene de la siguiente expresión:Por otra parte, para Qi(x,t)
Se ha demostrado que para el análisis transitorio con una mezcla homogénea de agua-aire, el valor de Qr(x, t)=0.03 permite la obtención de buenos resultados [58]. Por tal motivo, este valor fue empleado para la implementación del modelo numérico.
El desarrollo matemático antes presentado es para evaluar los nodos interiores, en este caso para simular las condiciones de frontera se utilizan las ecuaciones características, las cuales han sido utilizadas con éxito para simular transitorios con flujo bifásico [58,59]
ydonde am es la celeridad en una mezcla homogénea de agua-aire y para obtener su valor se puede usar la siguiente expresión:Los parámetros φ1, φ2 y φ3 se definen como:
y5Caso de estudioCarmona et al.[60] reportan el control de transitorios hidráulicos por el corte repentino de energía en una planta de bombeo, mediante la entrada de aire al acueducto El Cuchillo–Monterrey, ubicado en el Estado de Nuevo León, México. El sistema tiene una longitud total de 23km, la tubería es de acero de 2.13m de diámetro; la planta de bombeo cuenta con 5 bombas más una de repuesto, para impulsar un caudal máximo de 6 m3/s. El sistema de control de transitorios lo conforman dos tanques unidireccionales y varias válvulas de admisión y expulsión de aire o ventosas, instaladas a lo largo de la tubería. Estos dispositivos resultaron insuficientes por haberse considerado durante la etapa de diseño un valor incorrecto del momento de inercia de los equipos de bombeo. Por lo tanto, se propuso la instalación de tres cámaras de aire o calderines en la descarga de las bombas para poder operar con las 5 bombas y poder controlar adecuadamente las presiones transitorias si se detienen simultáneamente todos los equipos de bombeo.
La necesidad de iniciar lo antes posible el funcionamiento del acueducto, obligó a ensayar una forma poco convencional de protección contra presiones transitorias. La solución fue operar 2 de las 5 bombas y permitir la entrada de aire a través de las ventosas localizadas a lo largo del acueducto. Antes de proponer la solución al organismo operador del sistema, se realizó una simulación numérica para analizar su factibilidad. Se encontró que se debía instalar una ventosa con diámetro de orificio de 15.24cm (6”) adicional en los cadenamientos o kilómetros 12+660, 13+660, 17+147 y 17+857, con el propósito de permitir el ingreso de un mayor volumen de aire, para que se pudieran formar cuatro bolsas de aire grandes en estos puntos y así poder controlar las presiones transitorias.
Después de instalar las ventosas, se realizaron mediciones en el acueducto para registrar las presiones transitorias generadas por el paro simultáneo repentino de dos equipos al bombear un gasto de 2.4 m3/s. Al comparar la simulación numérica y los datos obtenidos en campo se observa una buena concordancia entre los resultados y se confirma que el ingreso de aire permite una protección satisfactoria.
Las simulaciones del transitorio con ingreso de aire a través de las ventosas se realizaron con un modelo numérico, que representa el proceso de ingreso del aire y su posterior compresión y expansión. La subrutina se basa en las ecuaciones que representan el fenómeno de separación de columna líquida propuestas por Chaudhry [38]. El proceso de expulsión de aire no es considerado durante las simulaciones, debido a que la eliminación del aire a través de las válvulas de expulsión o purgadores es un proceso muy lento comparado con su admisión.
Con el propósito de validar el modelo numérico propuesto en este artículo, se realizó la simulación del mismo transitorio descrito por Carmona et al.[60]. Se cuenta con todos los datos, incluidos los volúmenes de las bolsas de aire grandes que ingresaron y permanecieron en los puntos altos de la conducción durante el transitorio generado por el paro repentino y simultáneo de dos equipos de bombeo.
Adicionalmente, se simuló este mismo transitorio considerando las bolsas de aire con una mezcla homogénea de agua-aire inmediatamente aguas abajo de las mismas. Como se conoce el volumen de aire de las cuatro bolsas que permanecieron en la conducción, se utilizó la ecuación (2) paracalcular los mismos volúmenes de aire, y de esta forma se encontró el tirante o calado al inicio del salto hidráulico para evaluar el coeficiente de aireación β.
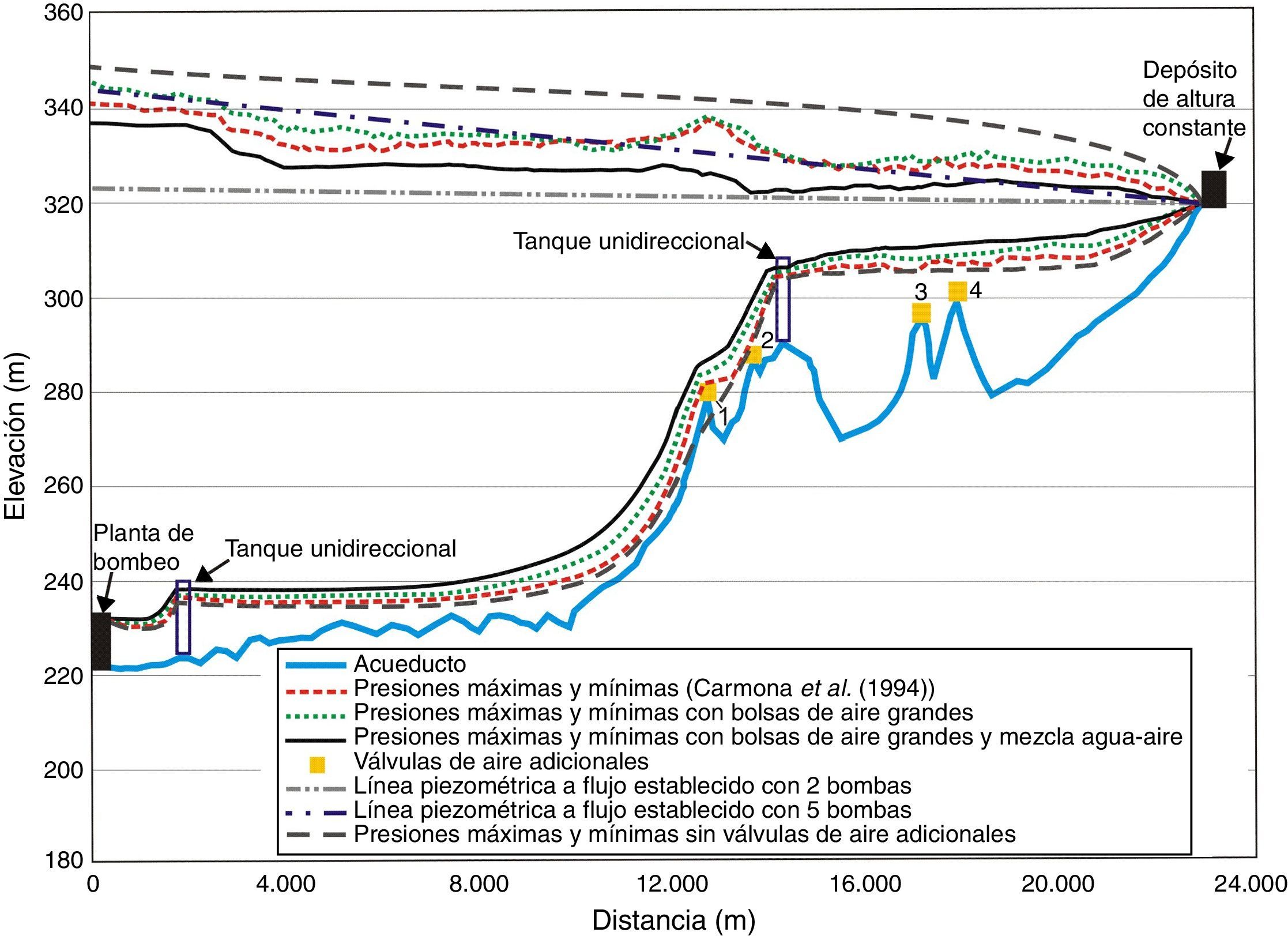
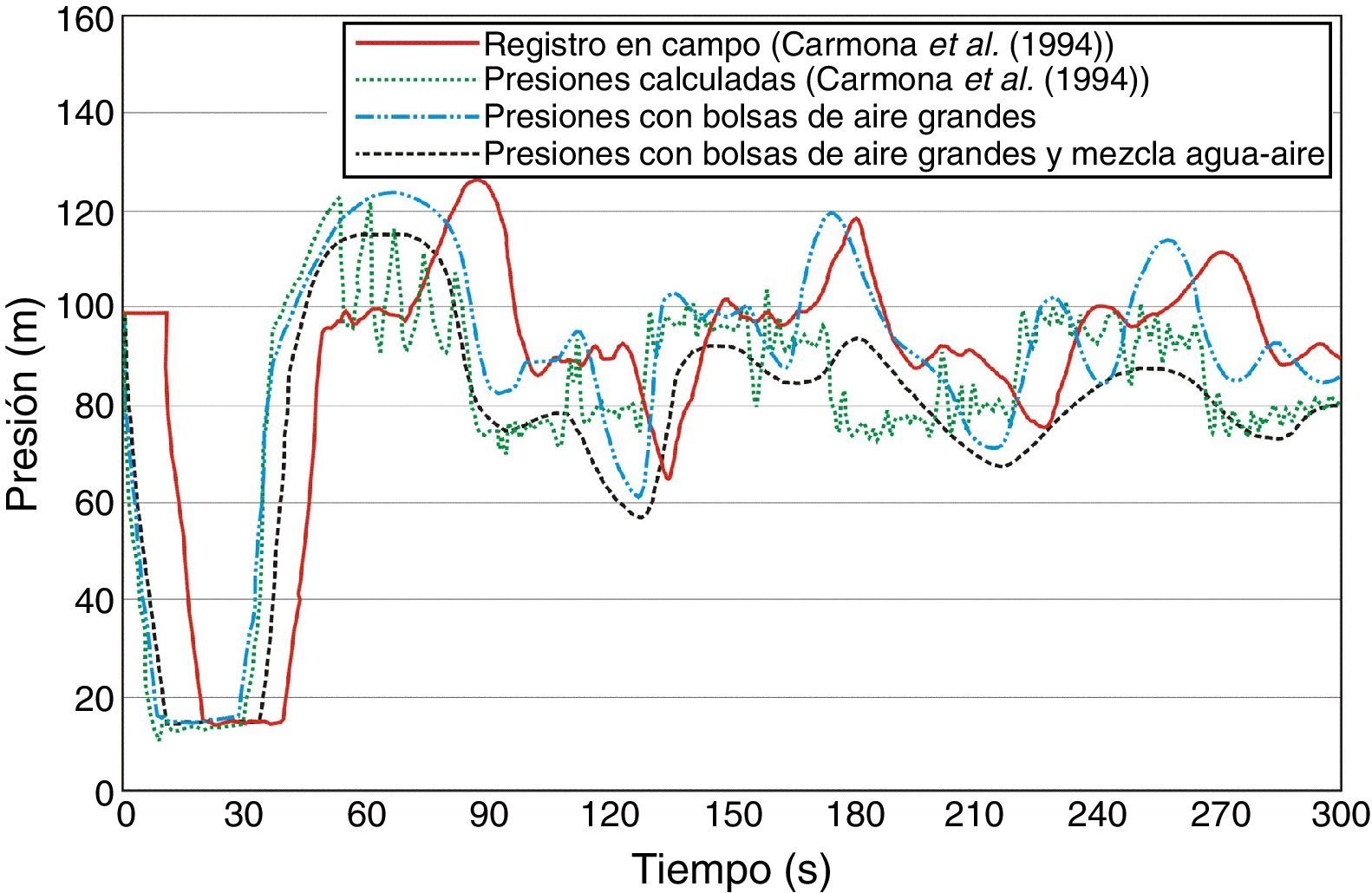
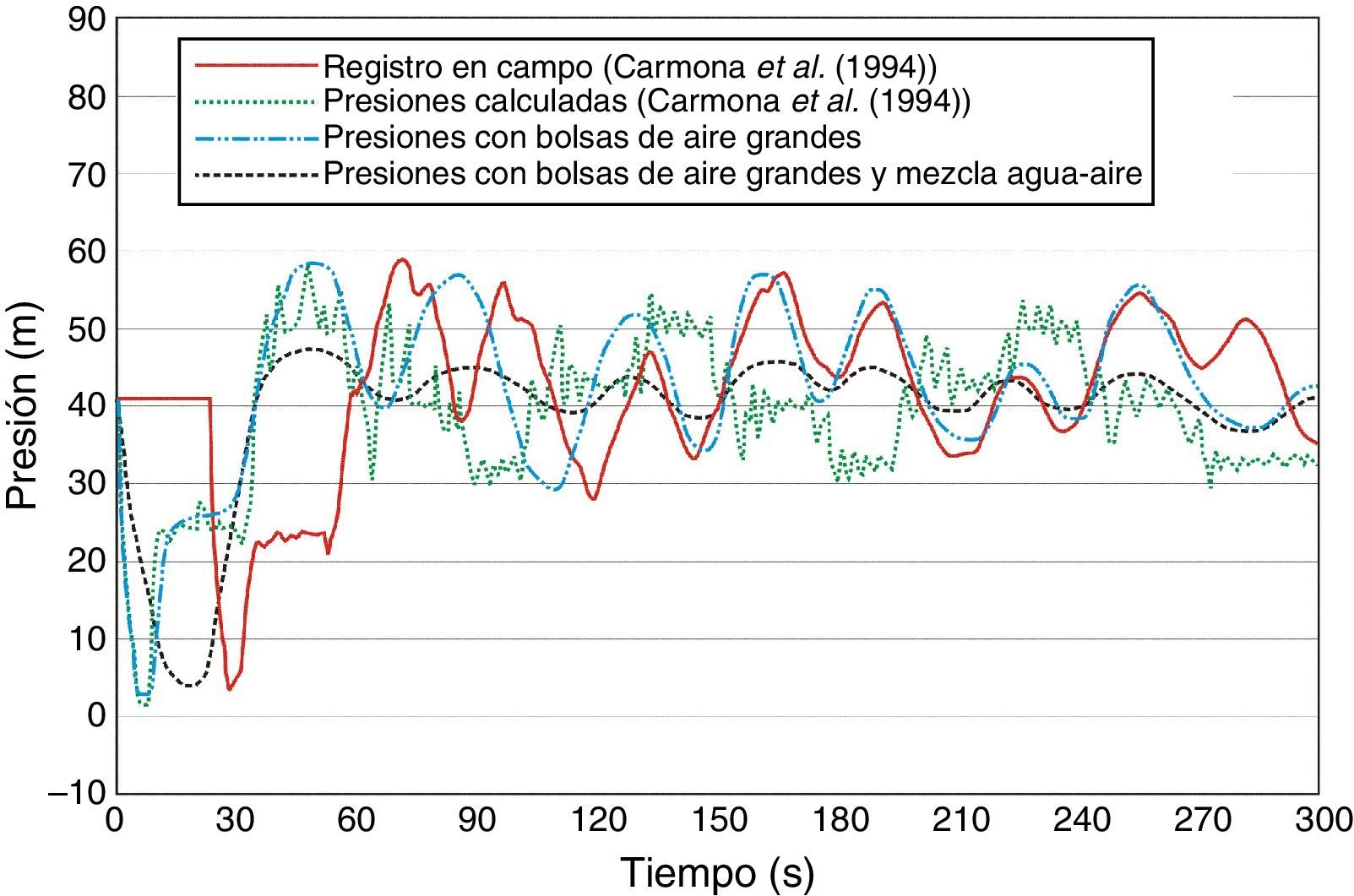
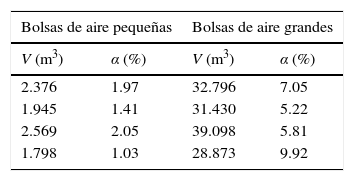
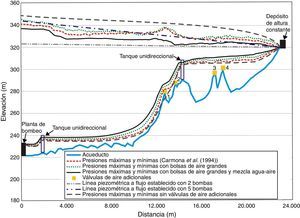
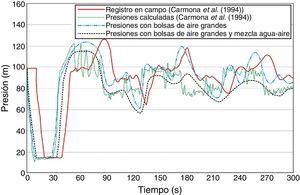
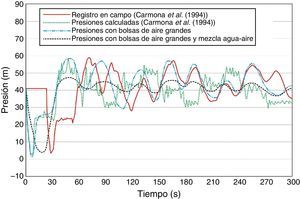
En la tabla 1 se resume la ubicación de los volúmenes de aire que se introdujeron al acueducto el Cuchillo-Monterrey durante el transitorio, y son los mismos que se consideran para la simulación, además se incluye la concentración de aire por volumen de agua en la mezcla homogénea α. En la figura 4 se muestran los resultados de las simulaciones, además en las figuras 5 y 6 se muestran los registros de presión medidos en campo durante el transitorio en la descarga de la bomba y en la ventosa ubicada en el kilómetro 12+660, así como los resultados obtenidos con los dos modelos numéricos.
Para poder hacer la comparación entre los efectos de las bolsas de aire grandes y pequeñas en transitorios hidráulicos, se siguió la metodología propuesta para encontrar los volúmenes de aire pequeños, tales que al generarse el transitorio con 2 equipos de bombeo produjeran efectos perjudiciales en el sistema. Primero se hizo un análisis con la ecuación (1) para identificar los puntos donde podrían acumularse las bolsas de aire pequeñas, y se encontraron 4 puntos los cuales coinciden con los sitios donde se formaron las bolsas de aire grandes. Asimismo, las ecuaciones (2) y (28) permitieron encontrar los volúmenes de aire contenidos en las bolsas y la concentración de aire por volumen de agua de la mezcla homogénea, respectivamente (ver tabla 1). Es importante mencionar, que en este caso se considera que no existen ventosas en los sitios donde se acumula el aire.
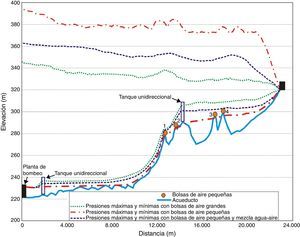
Después de una serie de simulaciones realizadas con el modelo numérico, se encontró que la situación más desfavorable para la conducción es cuando las 2 bombas están operando y las 4 bolsas de aire pequeñas se acumulan en los puntos 1 a 4, tal como se muestra en la figura 7.
6Análisis de resultadosEn la figura 4 se presentan los resultados obtenidos por Carmona et al.[60] durante la simulación del transitorio hidráulico, cuando dos bombas fallan simultáneamente y se permite la entrada de una cantidad importante de aire a través de las ventosas. Además, se presentan las envolventes máximas y mínimas obtenidas con el modelo numérico propuesto en este artículo, al considerar las cuatro bolsas de aire grandes localizadas en los puntos 1 a 4, con y sin una mezcla homogénea de agua-aire inmediatamente aguas abajo de las bolsas. En la gráfica también se muestran las líneas piezométricas en flujo establecido sin considerar aire atrapado, cuando operan 2 y 5 bombas. De los resultados mostrados, se puede concluir que existe una buena concordancia entre las envolventes de las presiones transitorias calculadas con ambos modelos al considerar las bolsas grandes.
Es importante mencionar que la envolvente máxima sin considerar válvulas adicionales en los puntos 1 a 4, en todo momento está por encima de la envolvente máxima obtenida al considerar bolsas de aire grandes, así mismo la envolvente mínima sin ventosas adicionales corta parte de la tubería, esto va a generar que el sistema experimente una presión menor a la atmosférica lo que podría conducir al fenómeno conocido como separación de columna líquida. Esto ocurriría cerca del cadenamiento 12+660.
Por otra parte, las ventosas adicionales en los puntos 1 a 4 admitieron la entrada de un mayor volumen de aire durante el transitorio, lo que permitió la formación de bolsas de aire grandes, en este caso las bolsas con y sin mezcla de agua-aire aumentaron las presiones transitorias mínimas para evitar una posible cavitación, que generaría el aplastamiento de la tubería en la vecindad del punto 1. En el mismo sentido, la envolvente de presiones máximas experimenta una amplificación en la zona donde están ubicadas las cuatro bolsas rebasando la línea piezométrica sin considerar aire atrapado, cuando operan 5 bombas, pero nunca rebasa la envolvente máxima que no considera ventosas adicionales. Al mismo tiempo, el efecto amortiguador producido por las bolsas de aire grandes y su respectiva mezcla de agua-aire es aún más benéfico comparado con la situación donde no se presenta la mezcla inmediatamente aguas abajo de las bolsas.
Es importante mencionar, que las mediciones realizadas en campo por Carmona et al.[60] han permitido probar la buena precisión del modelo numérico propuesto, para calcular transitorios hidráulicos con aire atrapado. En las figuras 5 y 6 se observa una muy buena concordancia entre los registros en la descarga de la bomba y la ventosa ubicada en el kilómetro 12+660, con los resultados obtenidos al considerar las bolsas de aire grandes con y sin la mezcla de agua-aire. Se debe señalar, que el registro de las presiones inicio segundos antes de que ocurriera el paro simultáneo de los equipos de bombeo, por lo mismo se observa el desfasamiento de las gráficas en las figuras 5 y 6. En la tabla 2 se resumen las presiones máximas registradas y las presiones máximas obtenidas con los modelos numéricos.
Comparación entre las presiones máximas registradas y las presiones máximas obtenidas con los modelos numéricos
| Posición en la que se hizo la medición | Registrada en el acueducto P(m) | Modelo con bolsas y sin mezcla P(m) | Modelo con bolsas y con mezcla P(m) | Modelo Carmona et al. (1994) P(m) |
|---|---|---|---|---|
| Descarga bomba | 126.60 | 124.05 (2.01%) | 116.10 (8.29%) | 123.53 (2.42%) |
| VAEA 12+660km | 58.50 | 58.20 (0.51%) | 48.10 (17.77%) | 57.98 (0.88%) |
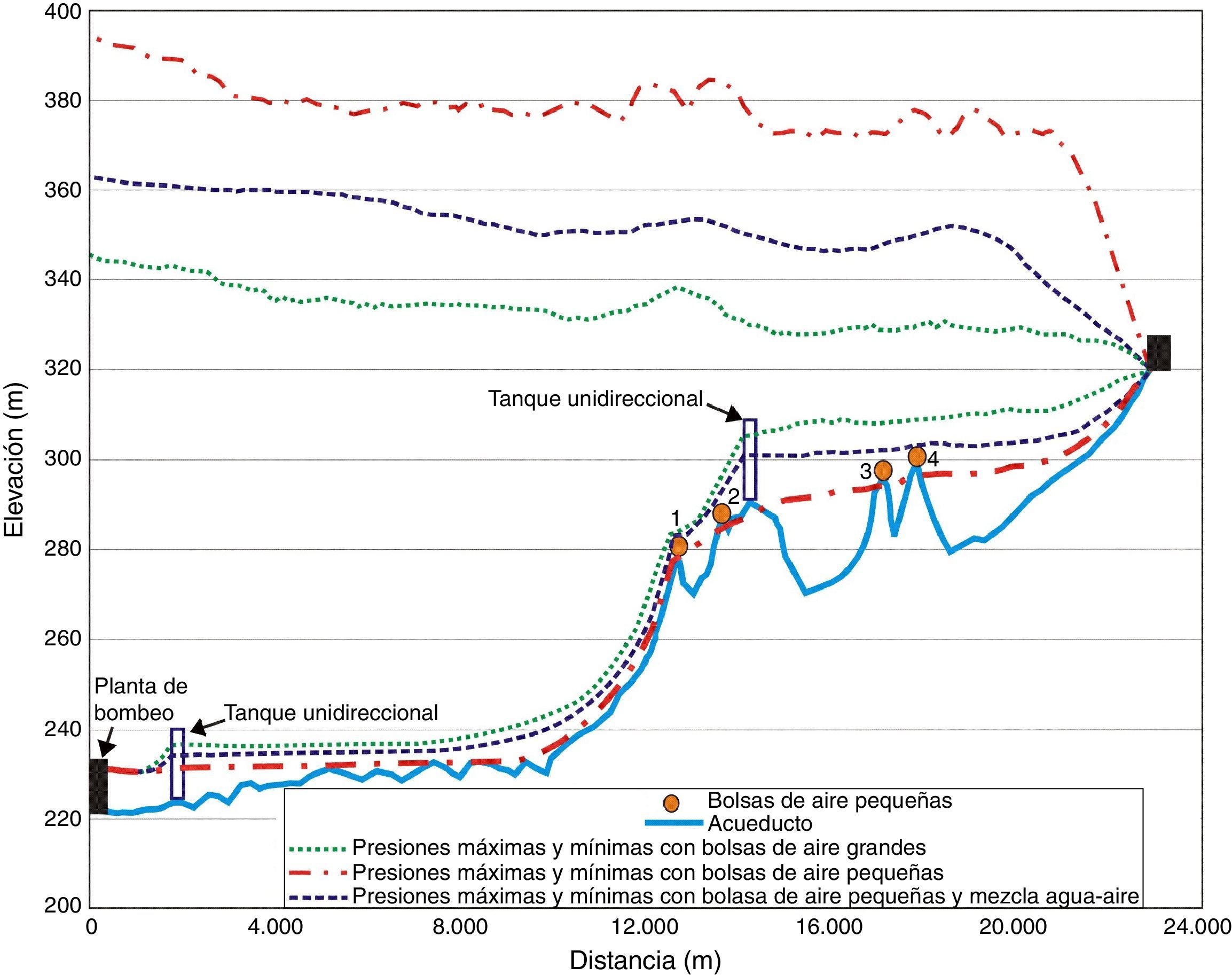
En la figura 7 se presentan los resultados obtenidos durante la simulación de los transitorios hidráulicos con las bolsas de aire pequeñas localizadas en los puntos 1 a 4, con y sin una mezcla homogénea de agua-aire inmediatamente aguas abajo de las bolsas.
De los resultados, se puede observar que el escenario más crítico se presenta con las cuatro bolsas de aire pequeñas sin mezcla de agua-aire. Los volúmenes de aire producen un aumento importante de las presiones máximas, produciendo un incremento aproximado de 50 metros de columna de agua en la descarga de las bombas, con respecto a la envolvente máxima considerando las bolsas de aire grandes. Asimismo, las amplificaciones más importantes ocurren en la vecindad de las cuatro bolsas de aire. En el caso de las presiones transitorias mínimas producidas por las bolsas de aire pequeñas, la envolvente corta varios puntos de la tubería del acueducto, por lo tanto se podría generar cavitación.
Cuando se consideran las cuatro bolsas de aire pequeñas con la mezcla de agua-aire la envolvente máxima se reduce significativamente. Aunque sigue notándose una reflexión en la vecindad de las bolsas, además las presiones continúan siendo mayores que las de la envolvente máxima considerando las bolsas de aire grandes. Por otra parte, se debe resaltar que al suponer las bolsas de aire pequeñas con la mezcla, la envolvente mínima no corta la tubería.
7ConclusionesEn este artículo se presenta una metodología para evaluar transitorios hidráulicos en acueductos con aire atrapado. Asimismo, el modelo numérico propuesto fue validado con los resultados obtenidos por otros autores y con mediciones de presiones hechas directamente en una impulsión. La comparación de las envolventes de las presiones transitorias muestran una muy buena concordancia. Lo que demuestra que el modelo es útil y puede ser utilizado durante la etapa de diseño, o bien para analizar acueductos en operación.
De los resultados obtenidos para el caso de estudio presentado, se puede concluir que las bolsas de aire pequeñas causan un incremento importante de las presiones máximas a todo lo largo del perfil del acueducto. Este fenómeno ocurre debido a que el aire tiene baja inercia que lo hace fácil de comprimir, es decir la densidad del aire es muy baja comparada con la del agua. Por el contrario, los transitorios hidráulicos reducen significativamente su valor, al incrementar el volumen de aire y el porcentaje de aire en la mezcla homogénea de agua-aire. Esto se debe a que un volumen de aire grande actúa como un amortiguador que ayuda a reducir las presiones transitorias.
Por todo lo antes descrito, es recomendable realizar un análisis detallado de todo conducto a presión, especialmente de aquellos que tienen un importante número de cambios de pendiente, para identificar posibles puntos de acumulación de aire. Se recomienda a los ingenieros relacionados con el diseño de impulsiones incorporar el análisis de aire atrapado a sus diseños, para así poder identificar los posibles escenarios que pueden llevar a problemas severos. En el mismo sentido, durante el análisis de transitorios hidráulicos se debe tener en cuenta, que todos los acueductos son dinámicamente diferentes en términos de su operación y configuración. Además, como resultado de los avances en la computación y los métodos numéricos, existe una tendencia de diseñar acueductos sólo mediante simulaciones numéricas. Sin embargo, el desarrollo de investigación experimental sería muy recomendable para realizar un estudio más riguroso del efecto del aire atrapado en transitorios hidráulicos.