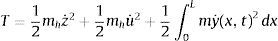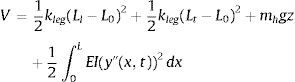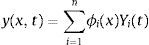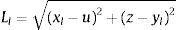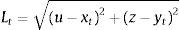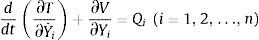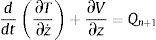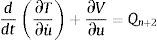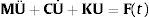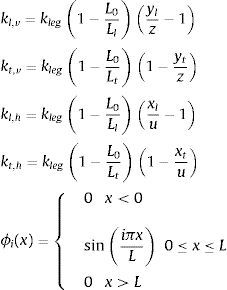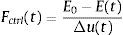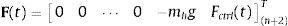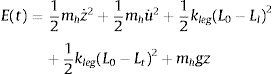Este trabajo se centra en evaluar la interacción del movimiento vertical entre un peatón y la estructura tipo viga por la que camina. Para lo cual, el peatón se ha modelado mediante un simple sistema dinámico que consiste en su masa concentrada a la altura del centro de gravedad soportada por dos muelles que simulan la rigidez de las piernas. El éxito de este modelo bípedo consiste en que las fuerzas de contacto resultantes se ajustan a las observadas experimentalmente para la marcha andando, lo que junto con el efecto de la masa móvil hace que la simulación sea realista. La respuesta dinámica de la viga se obtiene mediante la técnica de superposición modal a la que se acoplan las ecuaciones debidas a la masa puntual añadida, siendo la excitación del conjunto la dada por las fuerzas que induce el modelo de peatón en los puntos de contacto en cada instante considerado. El conjunto de ecuaciones diferenciales resultante se resuelve numéricamente mediante métodos de Runge-Kutta. Se presentan los resultados correspondientes a dos casos para diferente relación entre el peso de la viga y del peatón para diferentes cadencias de paso.
This work focuses on evaluating the vertical movements that appear when a pedestrian is walking on a slender beam-like structure. For that, the pedestrian is modelled by a dynamic system consisting on a concentrated mass, located in its center of masses, supported by two springs which simulate the stiffness of the legs. The success of this simple mechanical model is that the resulting contact forces are well adjusted to those observed experimentally for human gait. In this way, the structure is undergoing the moving mass and is loaded with realistic forces, resulting in a proper assembly to study interaction effects. The dynamic response of the beam is obtained at any coordinate by the modal superposition method, considering a finite number of modes. Differential equations of the resulting coupled problem are solved using proper numerical techniques. Solutions obtained for different scenarios (depending on the mass of the pedestrian with respect to the mass of the beam and on the pace) are presented.
La interacción persona-estructura es un tema importante en el diseño de estructuras esbeltas ocupadas y excitadas dinámicamente por personas ya que podría condicionar el estado límite de servicio respecto a vibraciones. A pesar de ello es un tema que desde el punto de vista computacional no ha sido abordado con la rigurosidad adecuada. En muchas ocasiones, incluso a propuesta de algunas normativas, se hacen formulaciones simplistas de fuerzas armónicas en las que se desprecia no sólo el efecto de la masa móvil sino también la correcta variación temporal de la excitación.
En este trabajo, la mecánica básica de la locomoción humana se asocia a un modelo bípedo masa-muelle y se comprueba que el considerar las piernas flexibles y la fase de doble soporte (ambas piernas apoyadas) es esencial para obtener los mecanismos básicos del movimiento del caminar humano. El modelo explica los cambios de las energías cinética y potencial que se observan al andar.
Este modelo, introducido por Whittington [9], mejora los modelos previos basados en el simple péndulo invertido [2,3] y permite tener en cuenta las dos fases de apoyo (simple y doble) lo cual genera no sólamente unas fuerzas verticales de contacto realistas, similares a las regristradas en una placa de fuerza, sino también una adecuada cinemática del centro de masas durante todo el ciclo de la marcha. Aunque existen otros modelos más complejos de peatón, incluyendo múltiples masas, efectos de amortiguamiento [3,7,8] o incluso modelos realistas multisegmento con masas distribuidas [6] se ha considerado que a nivel conceptual el modelo bípedo adoptado es suficientemente preciso para estudiar el problema acoplado objeto de este trabajo.
Aunque la formulación de dicho modelo, sin amortiguamiento alguno, “caminando” sobre un suelo rígido no precisa aporte de energía, cuando se acopla a una estructura flexible, principal esfuerzo realizado en este trabajo, es necesario introducir fuerzas adicionales para mantener la cadencia de paso. Ello es debido a que la estructura, en su movimiento, adquiere energía cinética (por vibración) y elástica (por flexión), además de la que disipa por el amortiguamiento estructural considerado [1,4]. Por ello el modelo aplica en cada instante al peatón una fuerza de control para compensar la energía que éste aporta a la vibración de la viga y para regular el ciclo de caminar del peatón. Los resultados de simulación muestran que la interacción dinámica aumenta con un mayor nivel de vibración de la estructura y, por lo tanto, requiere mayor aporte de energía para mantener el paso. Por otro lado, también se comprueba cómo se ve afectado el fenómeno de resonancia de la viga debido a la interacción dinámica [7,8].
La estructura que se considera en este trabajo consiste en una viga simplemente apoyada solicitada a flexión en el plano vertical por el efecto del caminar de un peatón (peatón activo) a través de las fuerzas que se desarrollan en los puntos de contacto del peatón al andar por dicha viga. En estas condiciones la estructura constituye un sistema lineal sometido a una excitación forzada cuya respuesta espacio-temporal se puede obtener mediante el método de superposición modal [5]. No obstante, al estar acoplado el modelo de peatón, el conjunto, por el efecto de la masa móvil, resulta no lineal y su resolución requiere técnicas especiales.
El trabajo se ha organizado de la manera siguiente: en primer lugar, tras esta introducción, se presenta la metodología empleada. A continuación, se diserta sobre los resultados obtenidos. Y en el último apartado se presentan las principales conclusiones que se deducen de este trabajo.
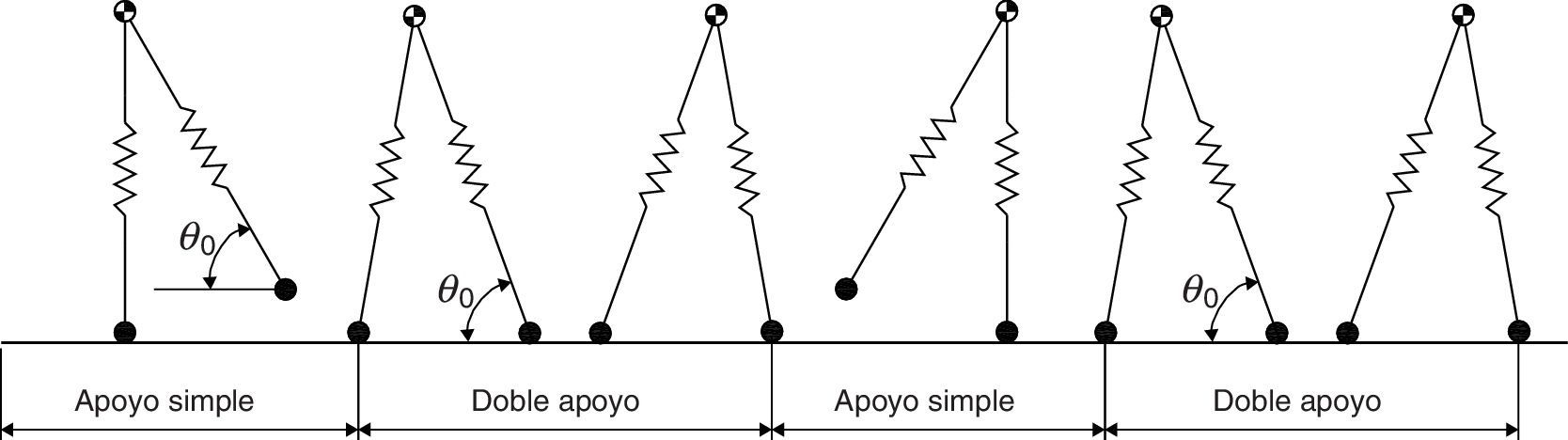
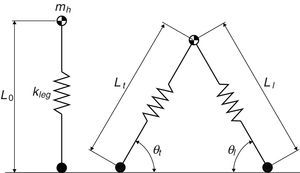
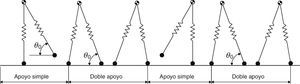
2Sistema dinámico peatón-estructuraEl peatón se simula con un modelo bípedo con dos grados de libertad como se muestra en la figura 1. El peatón se modela como una masa concentrada mh en el centro de masa (COM) y las dos piernas se describen como dos muelles de rigidez constante kleg sin masa y longitud inicial sin tensión L0[3].
Un paso completo se divide en dos períodos: fase de apoyo simple y fase de doble apoyo. En la figura 2 se muestra cómo la fase de doble apoyo comienza con el apoyo de la pierna guía y termina con la pérdida de contacto de la pierna de arrastre, instante en que se inicia la fase de apoyo simple. Entonces, conforme se avanza la pierna de arrastre se vuelve a situar por delante del COM con un ángulo de ataque determinado θ0 y se convierte en la pierna guía de la siguiente fase. Cuando dicha pierna contacta con el suelo, la fase de apoyo simple se ha completado. Nótese que con estas consideraciones no es necesario distinguir entre pierna izquierda o derecha y un paso completo se compone de dos sucesiones de las fases de apoyo simple y doble.
Por simplicidad, pero sin pérdida de generalidad, se ha considerado que la estructura es una viga biapoyada en los extremos de sección transversal constante, cuyo comportamiento a flexión viene gobernado por las ecuaciones de Navier-Bernoulli.
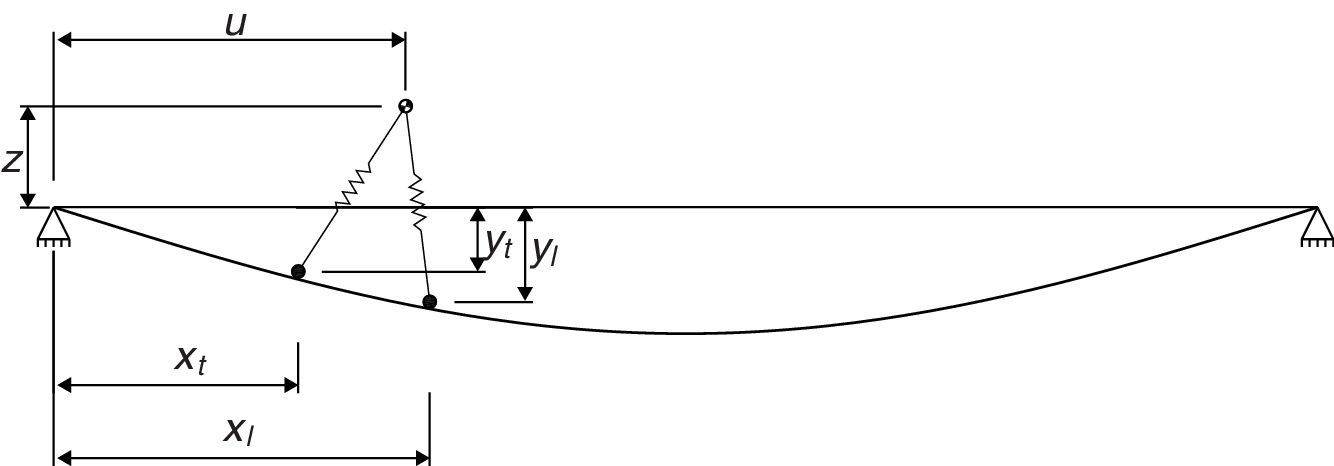
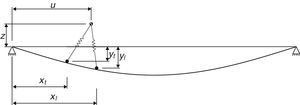
2.1Ecuaciones del movimientoConsidérese la estructura sometida al efecto de un peatón caminando, como se muestra en la figura 3. Se asume que el peatón se mantiene en contacto con la superficie de la viga en todo momento.
Las ecuaciones de movimiento que gobiernan la vibración se derivan de la ecuación de Lagrange. La energía cinética T y la energía potencial V del sistema dinámico peatón-estructura en la fase de doble apoyo se pueden obtener como:
El movimiento del COM se describe por las coordenadas generalizadas (z, u), donde z y u indican los desplazamientos vertical y horizontal, respectivamente; y(x, t) es el desplazamiento de la viga; E y m son el módulo de Young del material y la masa por unidad de longitud de la viga; g es la aceleración de la gravedad; Ll y Lt son la longitud de dos piernas, respectivamente, los subíndices “l” y “t” indican las piernas guía y de arrastre, respectivamente; y′′(x,t) es la curvatura de la viga.
Por el método de superposición modal, el desplazamiento vertical de la viga se puede expresar como
donde ϕi(x) son los n primeros modos de vibración considerados e Yi(t) son las coordenadas modales.La longitud de la pierna guía y de la pierna de arrastre son, respectivamente:
donde yl y yt son el desplazamiento vertical de la viga en los puntos de contacto de las piernas; xl y xt son la posición horizontal de la pierna guía y la pierna de arrastre, respectivamente.Las ecuaciones de Lagrange del sistema peatón-estructura vienen dadas entonces por
Sustituyendo (1) en (4) da como resultado la ecuación dinámica del sistema en forma matricial como (5):
donde M, C, K, U, U˙, U¨ y F(t) son las matrices de masa, amortiguamiento y rigidez, y los vectores de desplazamiento, velocidad, aceleración y fuerza, respectivamente. Para el caso de interés, las matrices de masa, amortiguamiento y rigidez y el vector de fuerza se pueden expresar comodondeSe observa que la matriz de rigidez es variable en el tiempo. Se puede comprobar a partir de (7) que (kl,v,kt,v) y (kl,h, kt,h) son la rigidez vertical y horizontal efectiva, respectivamente. La rigidez vertical efectiva se determinada a partir de una combinación de la rigidez de la pierna (kleg), el desplazamiento del COM (u, z) y el desplazamiento de la estructura (y). Por lo tanto, las ecuaciones del movimiento del sistema peatón-estructura se acoplan en términos de la fuerza de interacción en el punto de contacto. Con el movimiento del peatón, la fuerza de interacción entre el peatón y la estructura cambia. Aunque la rigidez de la pierna (kleg) es constante durante la marcha, la rigidez efectiva de la pierna es no lineal y los puntos de contacto también varían, haciendo que el problema dinámico sea no lineal.
Todo el análisis anterior se basa en la fase de doble apoyo. El proceso de análisis de la fase de apoyo simple es similar a la de la fase de doble apoyo haciendo todos los coeficientes relativos a la pierna de arrastre iguales a cero en dicha fase.
2.2Aporte energético al sistemaEl modelo de peatón empleado es capaz de reproducir la marcha del caminar humano pero requiere un aporte de energía para mantener el ciclo ya que se cede energía a la viga que además parcialmente se disipa por amortiguamiento [9]. Una posible forma de proporcionar esta energía es aplicar una fuerza de control de manera directa al peatón [3]. Esta fuerza se evalúa a partir del requisito de que el trabajo externo aportado debe compensar la energía perdida, resultando:
Esta fuerza debe ser considerada en (6) de la forma,
En las expresiones anteriores Fctrl(t), E0, E(t) y Δu(t) son la fuerza horizontal de control, la energía inicial del peatón, la energía del peatón y el incremento de desplazamiento horizontal del COM en el instante “t”, respectivamente.
La energía total del peatón E(t), incluyendo la energía potencial y la energía cinética está dada por
2.3Análisis modalComo es bien sabido para aplicar el método de superposición modal debe realizarse un análisis modal previo, con el objetivo de determinar las frecuencias propias de la estructura objeto de análisis y sus modos propios asociados convenientemente escalados. Todo ello, para el caso de la viga biapoyada está perfectamente documentado y responde a expresiones analíticas cerradas y simples, véase por ejemplo [5].
2.4Proceso de análisisLa respuesta dinámica del sistema acoplado en cada paso de tiempo “t” se puede obtener en los siguientes pasos:
- 1.
Entrada de los parámetros geométricos y físicos tanto del modelo de peatón como de la viga.
- 2.
Realizar un análisis modal para obtener las frecuencias y los modos de vibración de la viga aislada y definir el número de modos a considerar.
- 3.
Definir las condiciones iniciales de la viga (en reposo generalmente) y del peatón (desplazamiento inicial y velocidad del COM, posición y situación de partida de la pierna guía).
- 4.
Construir las matrices de masa, rigidez y amortiguamiento en el instante inicial.
- 5.
Definir el incremento de tiempo y otros parámetros del proceso de integración.
- 6.
Para cada paso de tiempo:
- a)
Determinar si está en la fase de doble apoyo o simple.
- b)
Determinar la posición de los pies y los puntos de contacto con la viga deformada.
- c)
Calcular los acortamientos de las piernas y su rigidez efectiva.
- d)
Ensamblar la matriz de masa, amortiguamiento y rigidez (dependiente del tiempo) y el vector de fuerza del sistema, incluyendo la fuerza de control.
- e)
Aplicar un método adecuado (Runge-Kutta de cuarto orden) para obtener la respuesta del sistema al final de cada incremento de tiempo.
- f)
Repetir hasta completar el tiempo bajo estudio.
- a)
Las condiciones iniciales de esta fase deben ser tales que se reproduzca el ciclo del caminar humano según se establece en la refencia [9].
3Resultados numéricosPara ilustrar las capacidades del modelo propuesto, se analizan dos ejemplos de interacción peatón-estructura.
3.1Ejemplo 1 - Viga rígidaSe considera una viga biapoyada de longitud L=11.0m, las propiedades de la viga son: rigidez EI=1.64·108Nm2, la masa por unidad de longitud m=1.364·103kgm−1 y se supone que los factores de amortiguamiento de todos los modos son iguales de valor ζi=0.3% [7]. Las propiedades del peatón son: mh=80kg, rigidez de ambas piernas kleg=20kN/m, ángulo de ataque θ0=69°, y velocidad media vm=1.2m/s que para los parámetros elegidos corresponde a una cadencia de fp=2.0 Hz. Se consideran los dos primeros modos en el análisis de la viga, donde las frecuencias naturales son: f1=4.501Hz y f2=18.006Hz y las masas modales son M1=M2=7502kg.
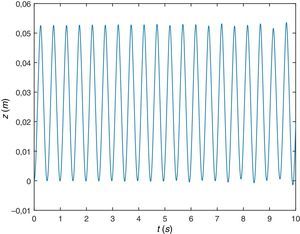
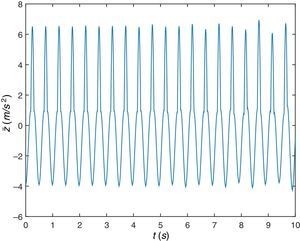
Las figuras 4 y 5 muestran la respuesta dinámica en la sección central de la viga, desplazamiento y aceleración, respectivamente. Y para este caso se comprueba, como parece lógico, que la respuesta es la misma considerando interacción dinámica que sin considerarla.
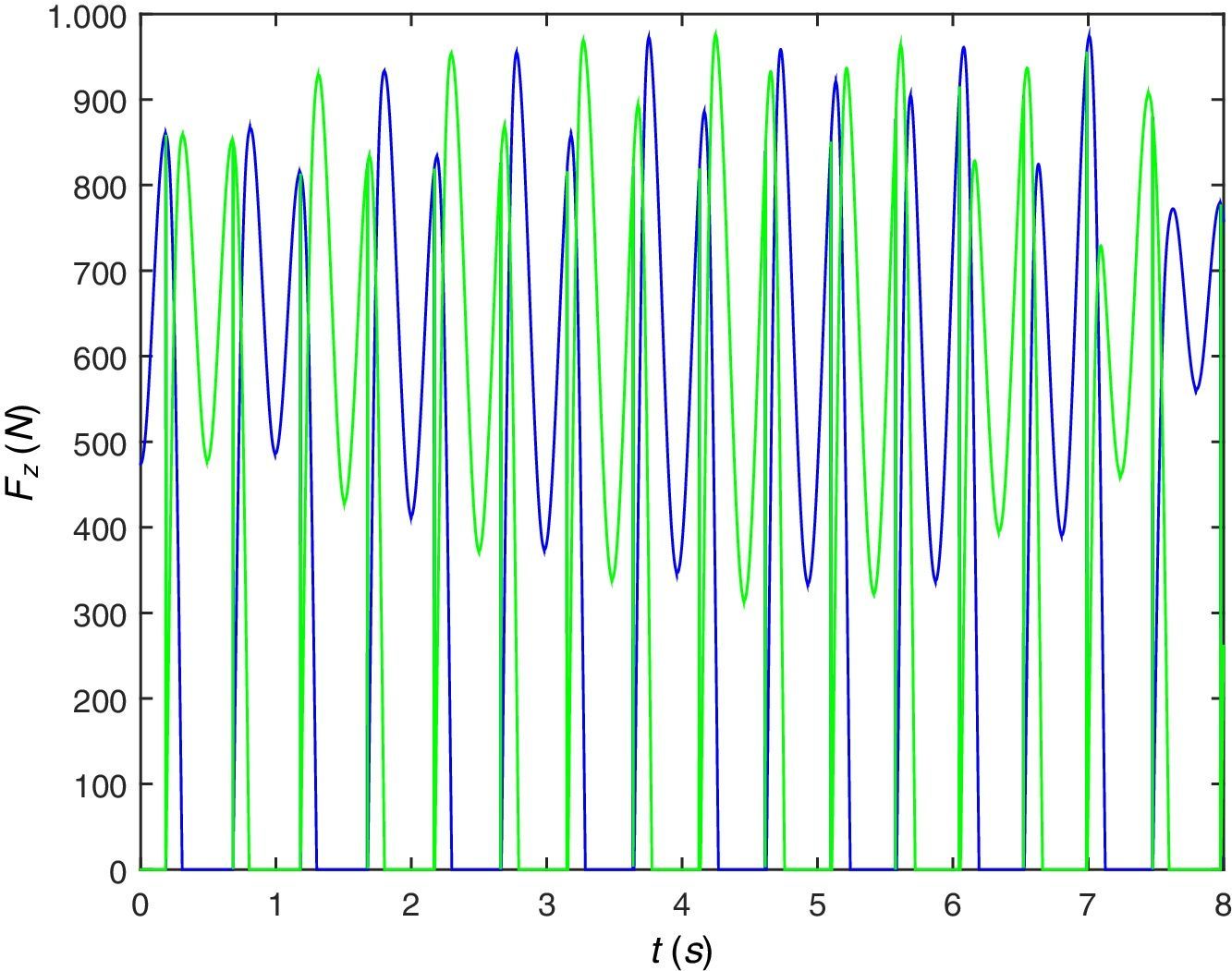
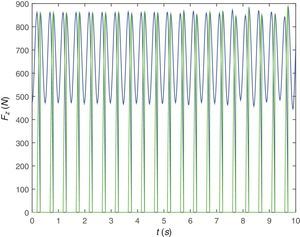
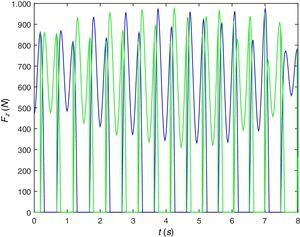
En la siguiente figura, la figura 6, se indica la fuerza que el peatón transmite a la viga. Para este caso de peatón caminando sobre viga rígida se comprueba que esta excitación se corresponde con la que se mide en una placa de fuerza.
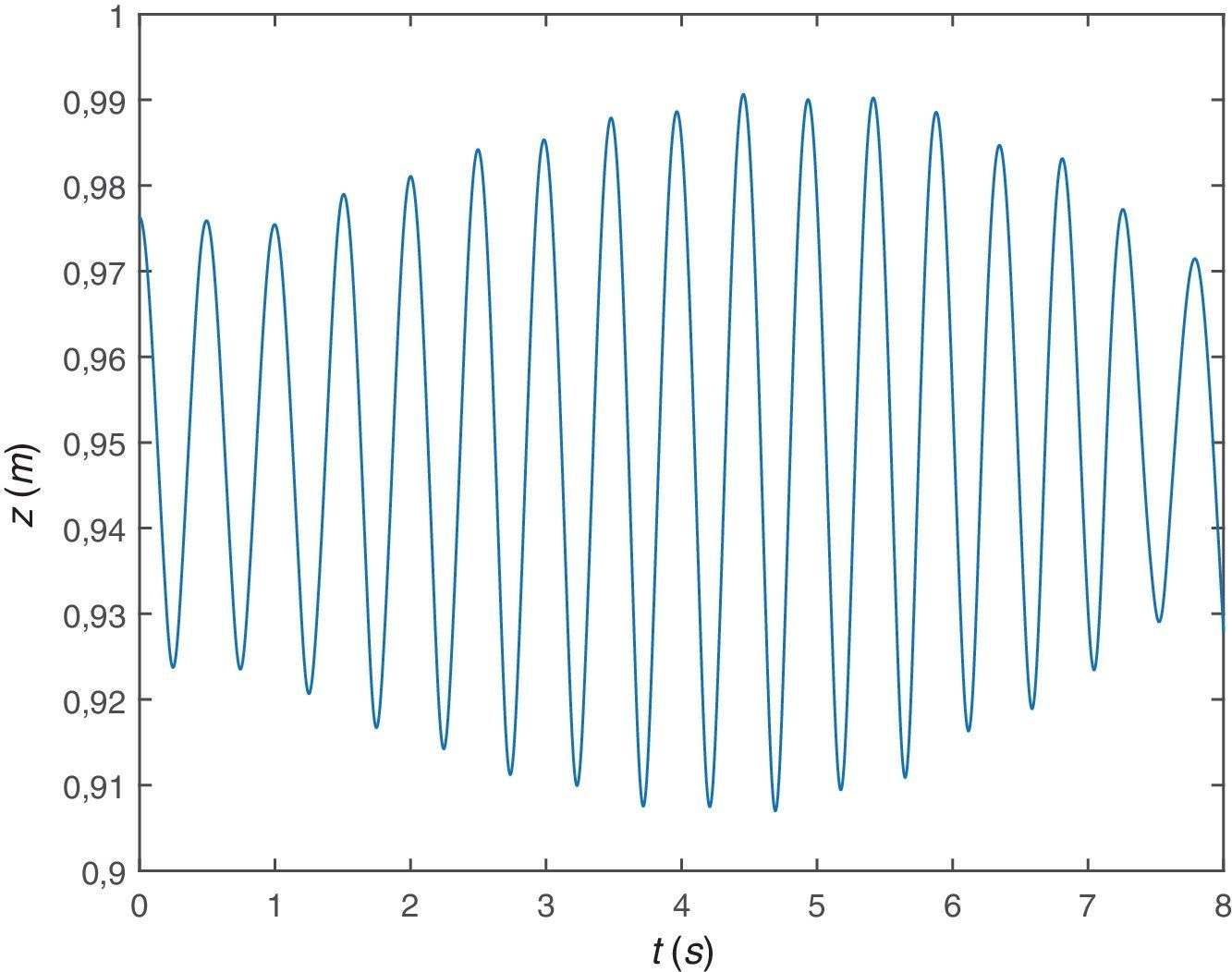
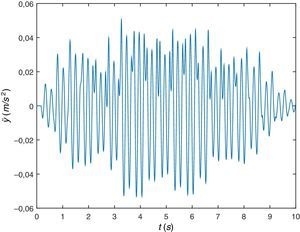
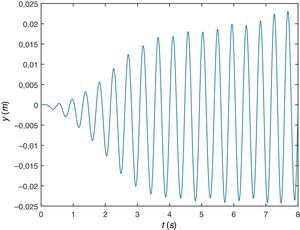
En las figuras 7 y 8 se representa gráficamente el desplazamiento vertical y la aceleración también vertical del centro de masa del peatón (COM). La curva que describe la primera gráfica es la cicloide que es el tipo de curva que se espera describa la trayectoria del COM, y los niveles de desplazamiento son del orden de unos 5cm que concuerda con los valores que se observan experimentalmente.
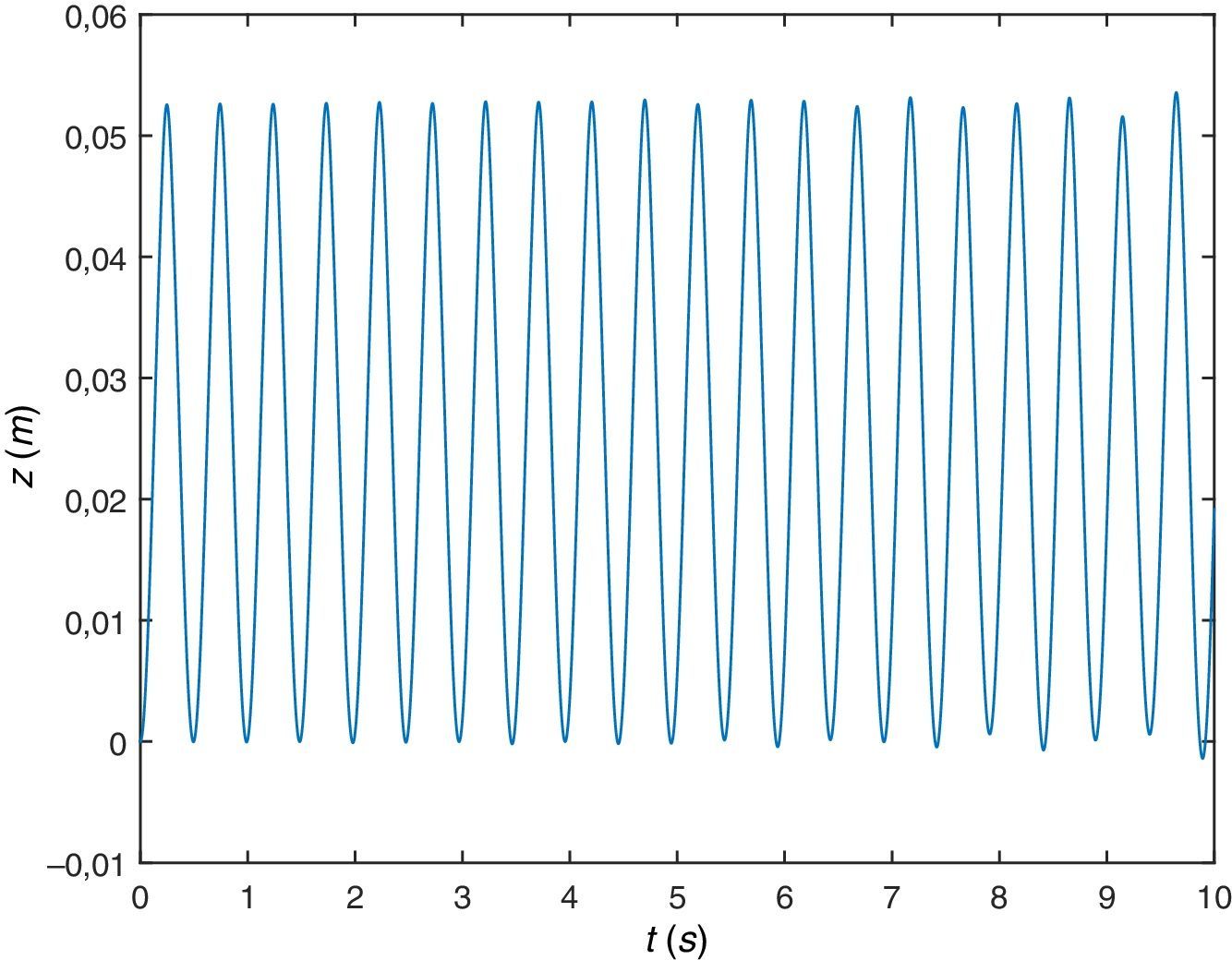
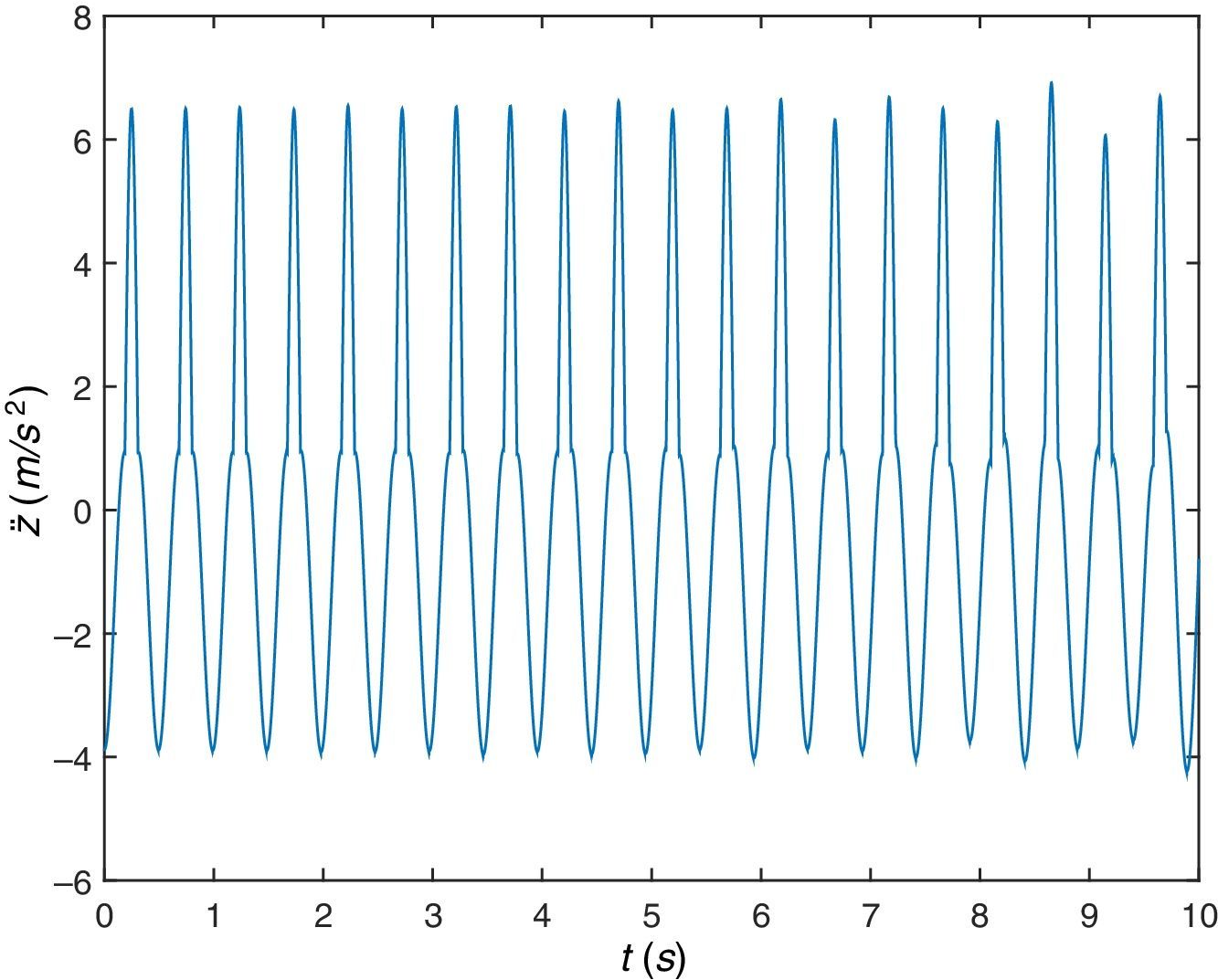
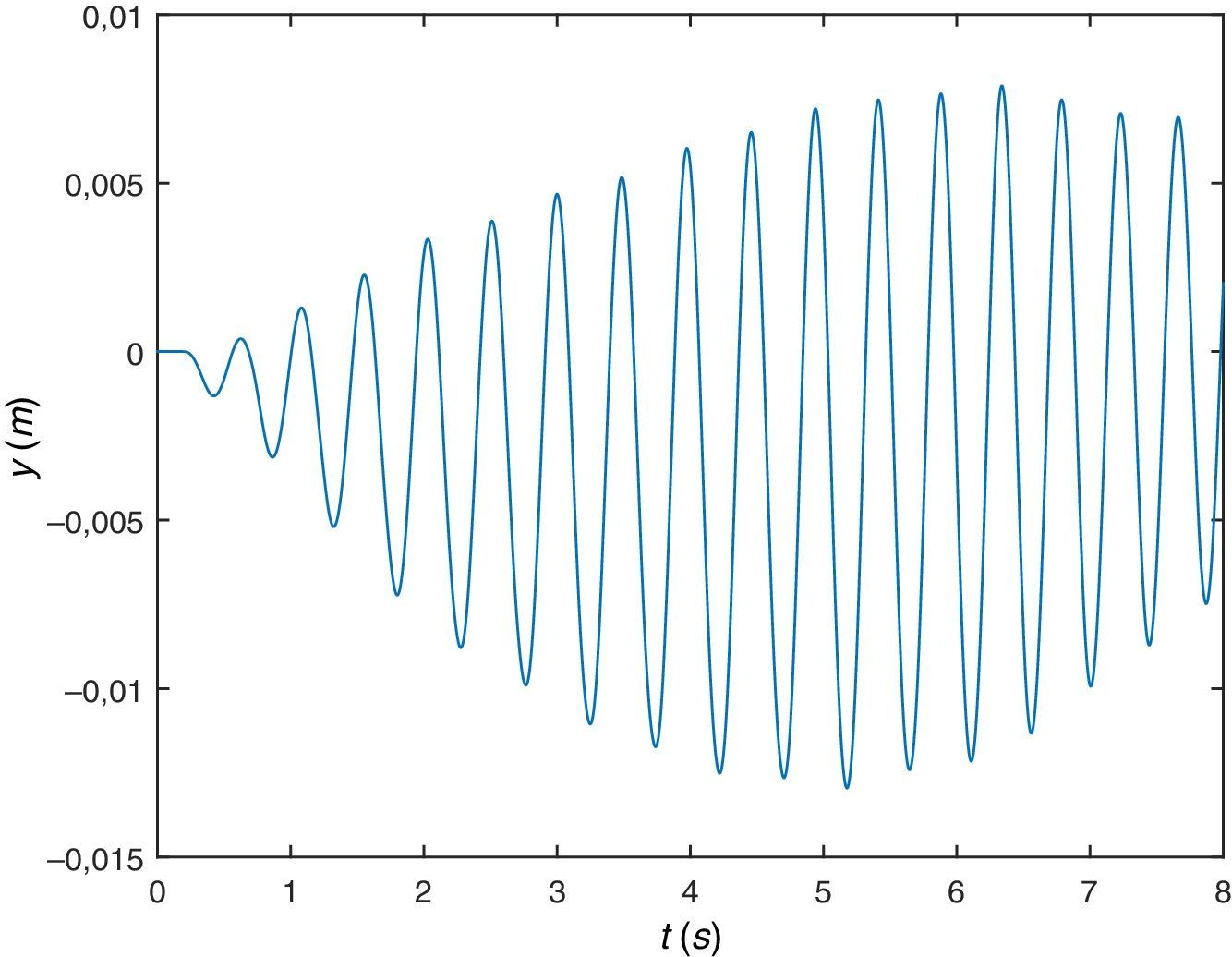
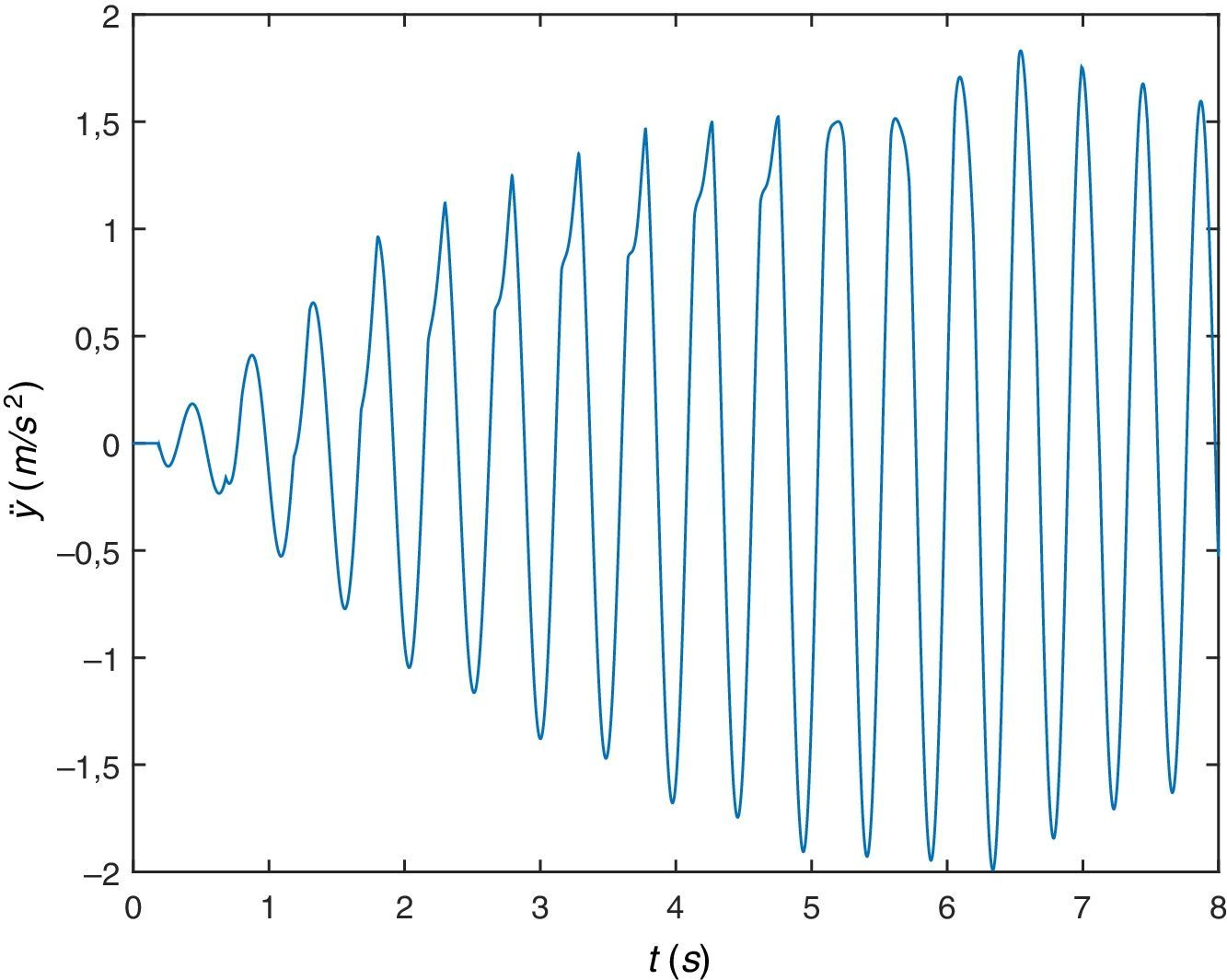
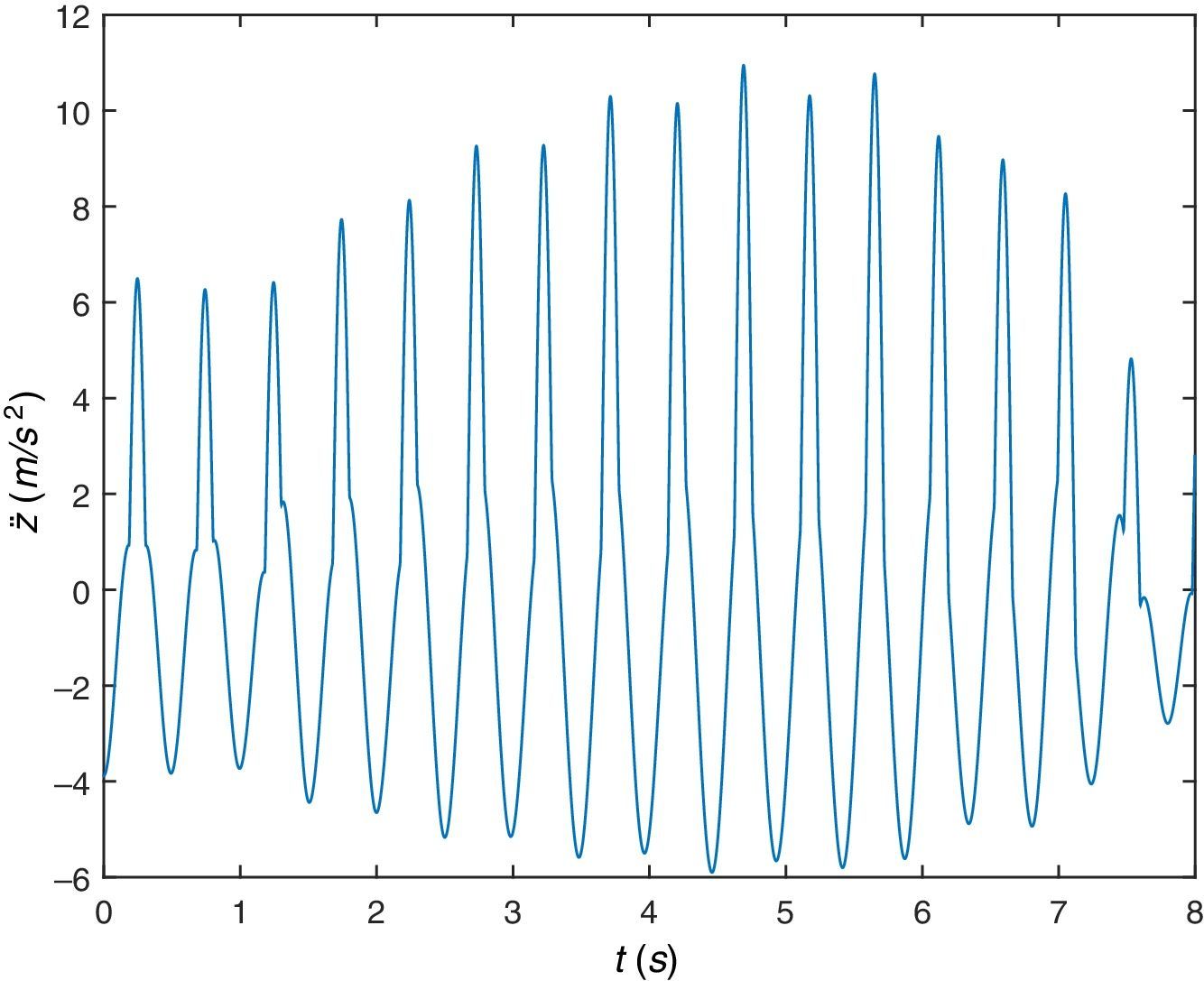
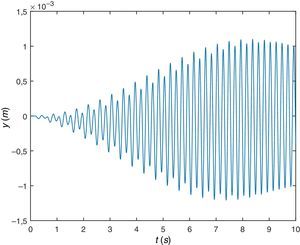
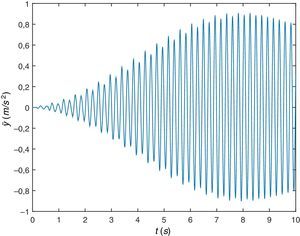
A continuación, se va a simular el peatón caminando sobre la misma viga pero a una frecuencia algo mayor, concretamente a la frecuencia de paso fp=2.25Hz. De la respuesta de la viga en desplazamientos o aceleraciones (figuras 9 y 10), se comprueba que tiene lugar el fenómeno de resonancia, amplificación de la respuesta por coincidencia de algún armónico de la excitación con alguna de las frecuencias naturales o propias de la estructura.
3.2Ejemplo 2 - Viga flexibleA continuación se considera una viga biapoyada de longitud L=9.0 m, ancho b=0.8 m y espesor e=0.12 m. Las propiedades del material de la viga son densidad ρ=2400kg/m3 y módulo de Young E=3·1010 Pa. La frecuencia fundamental de la viga es 2.375 Hz. Los datos del peatón son exactamente los mismos del primer ejemplo.
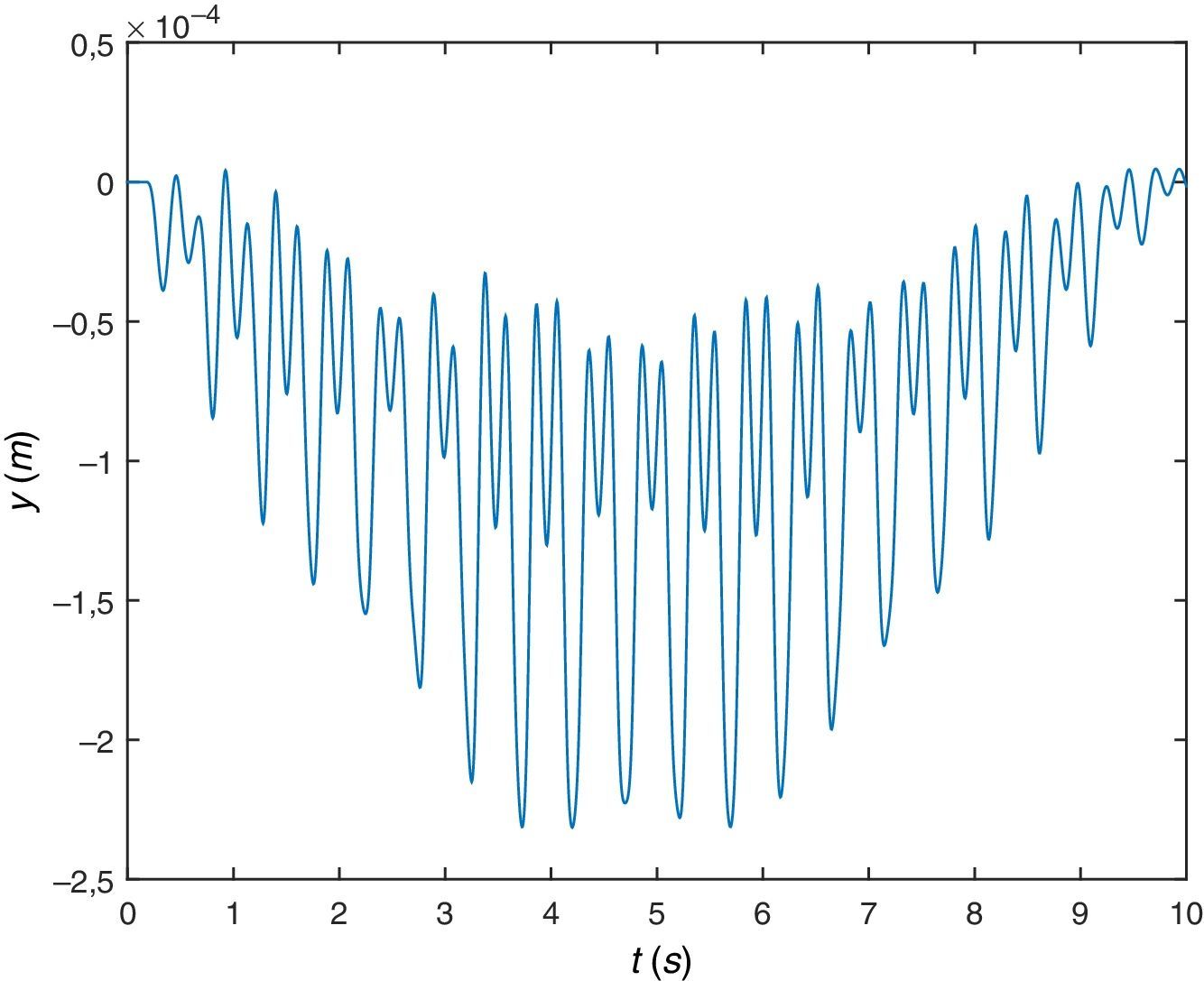
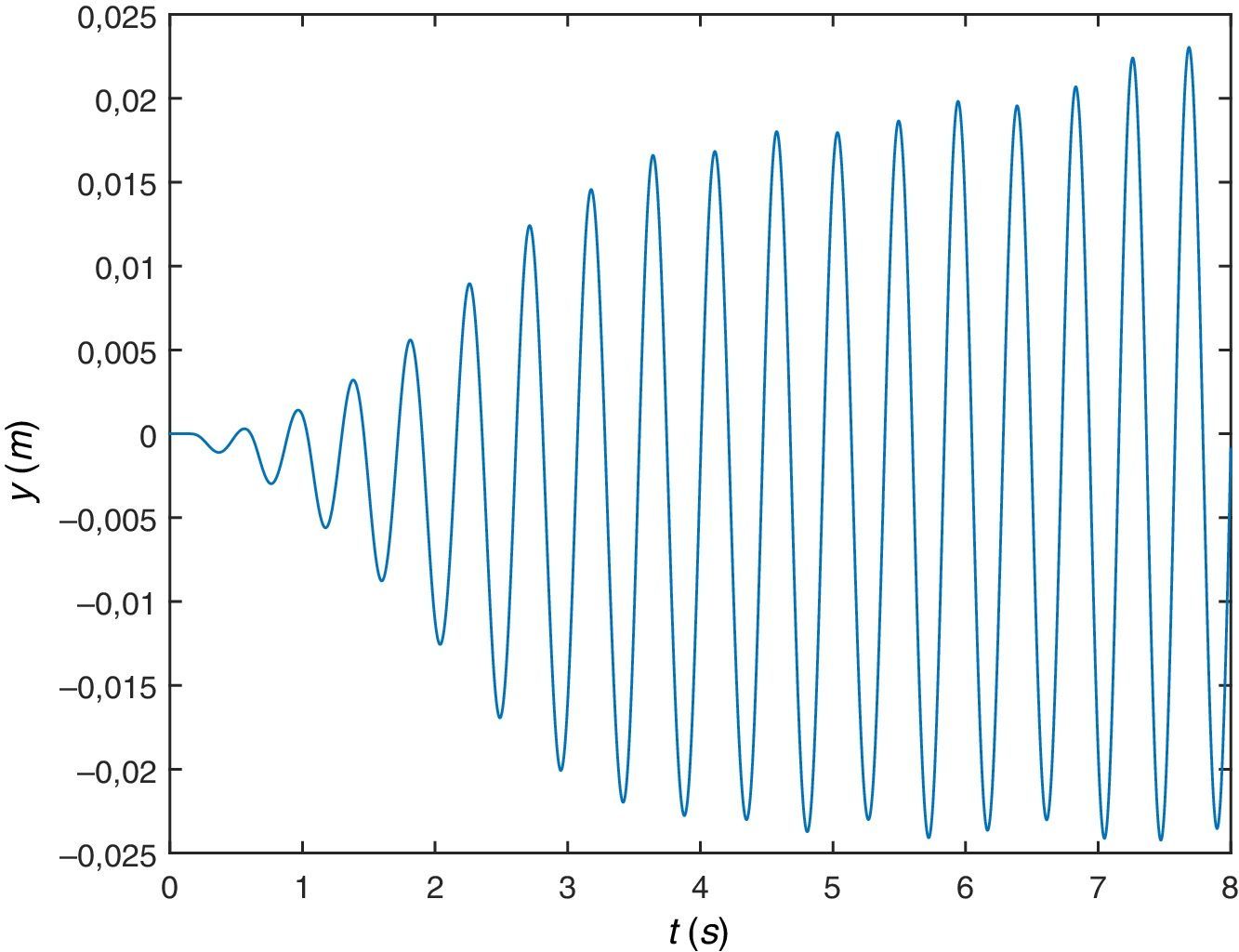
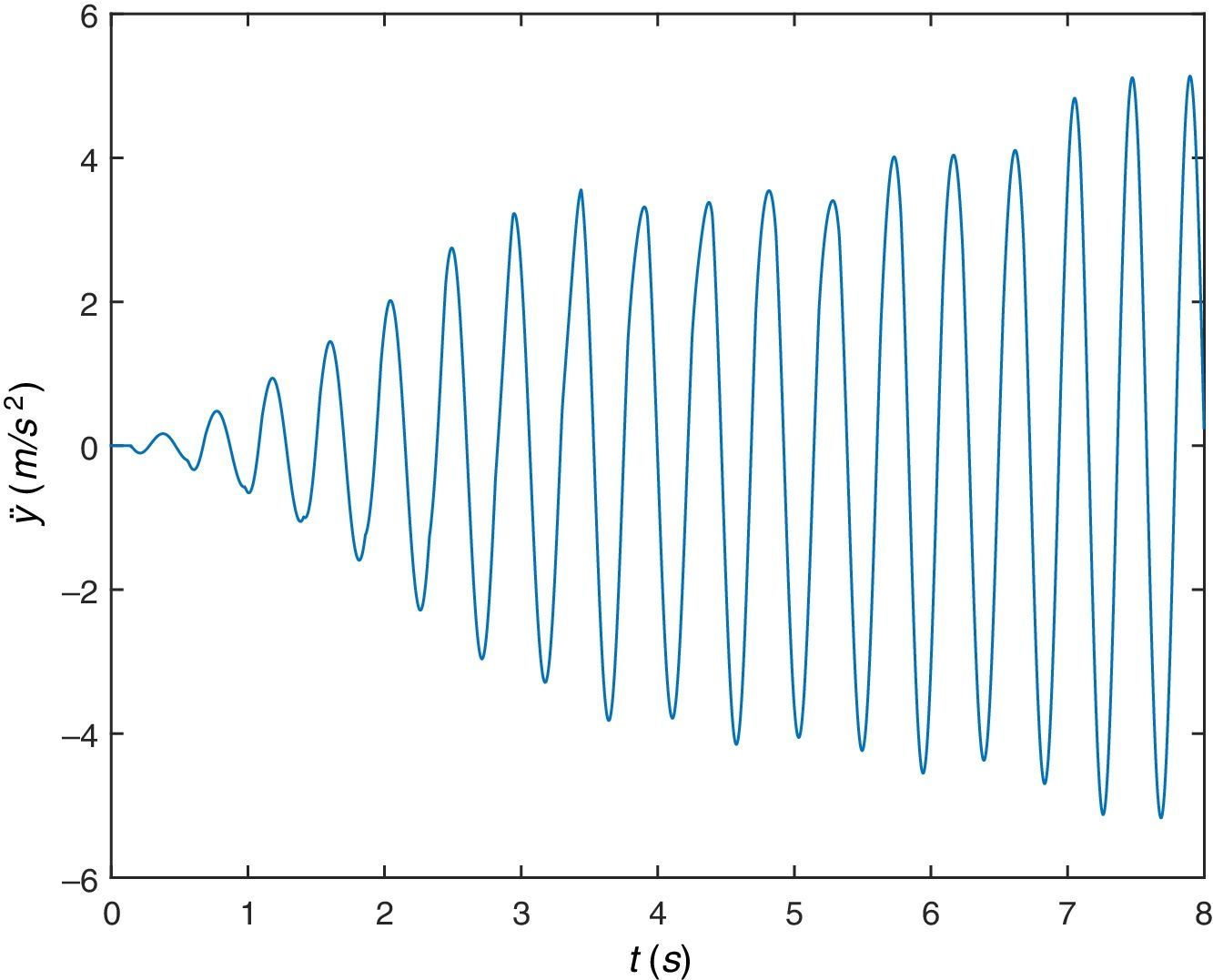
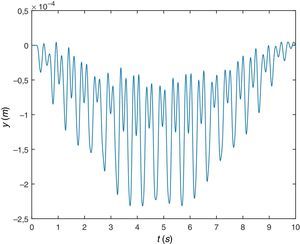
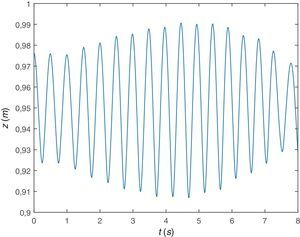
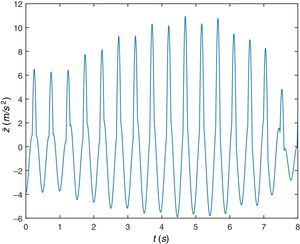
Igual que antes, de nuevo, en primer lugar se muestra la respuesta dinámica de la viga en su sección central, figura 11, desplazamiento y figura 12, aceleración. Se observa que aunque esta viga pudiera suponerse suficientemente rígida (desde el punto de vista de la Resistencia de Materiales), empieza a haber diferencia entre considerar la respuesta del sistema teniendo en cuenta la interacción dinámica peatón-estructura o sin tenerlo en cuenta, existe diferencia apreciable, se trata de una viga flexible (desde el punto de vista del presente trabajo).
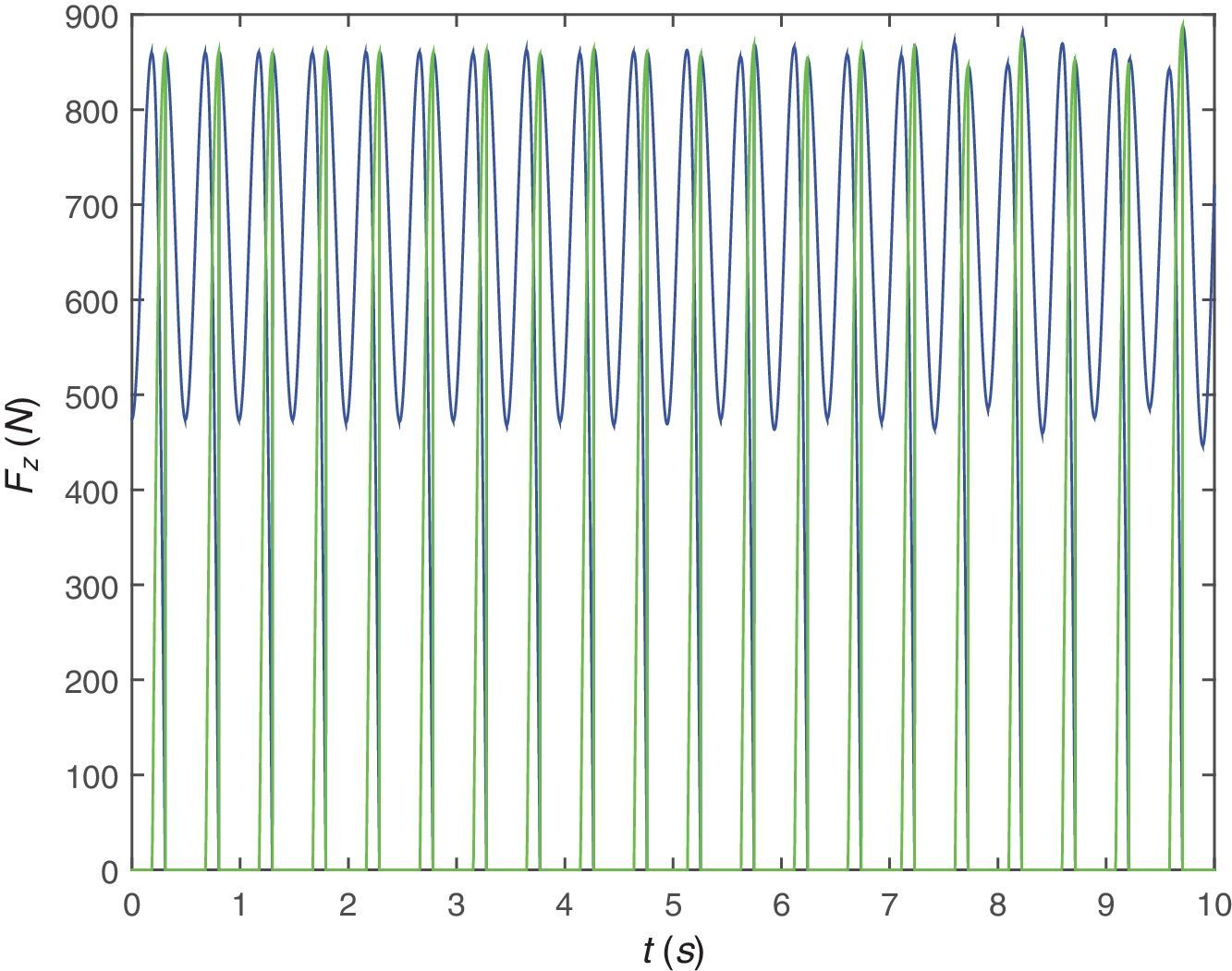
La figura 13 presenta la evolución a lo largo del tiempo de la fuerza vertical de contacto de cada uno de los pies del peatón con la estructura. Aunque todavía se parece mucho a lo medido con una placa de fuerza se puede observar cierta diferencia sobre todo en la parte central, cuando el peatón transita por el centro del vano de la viga.
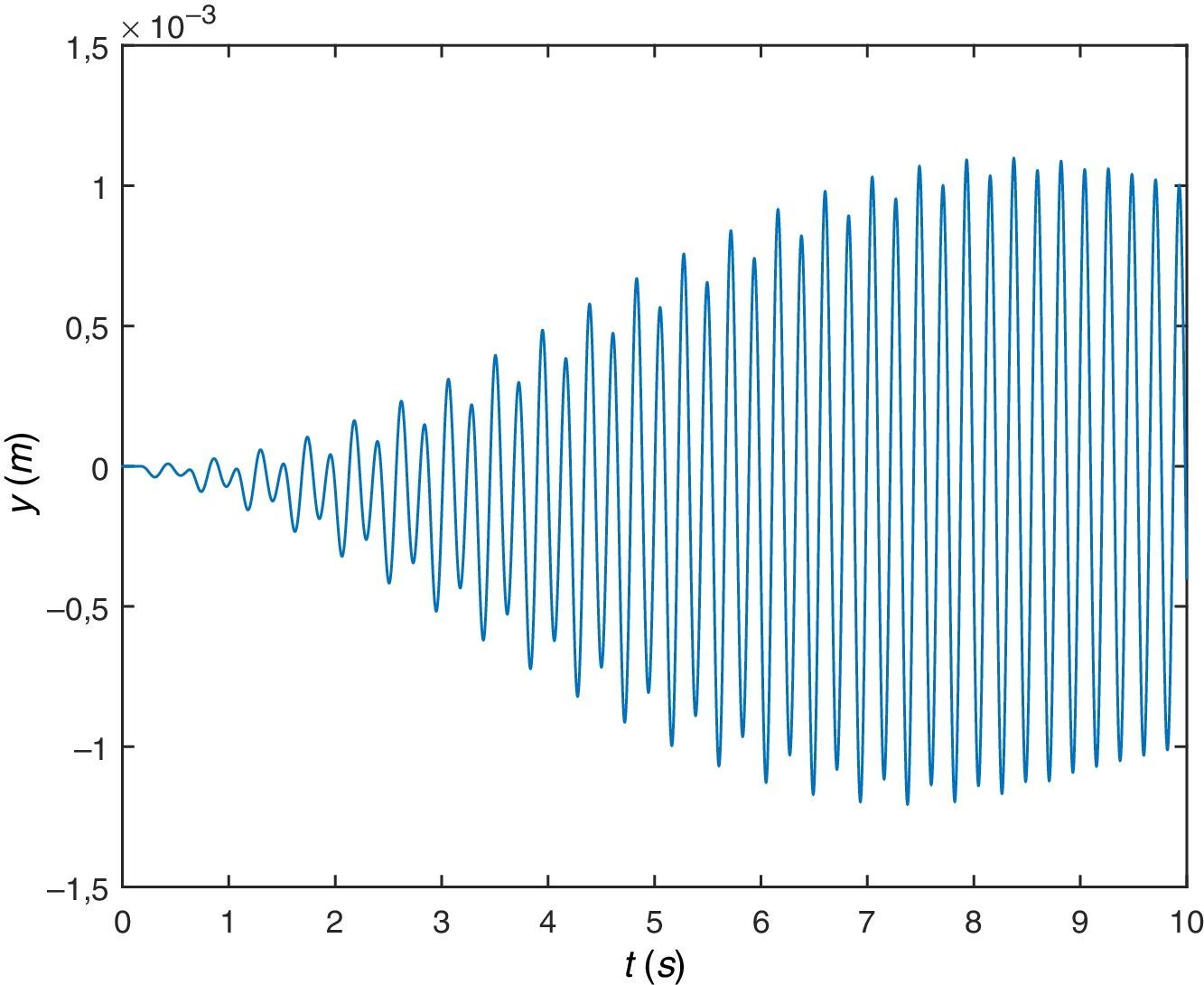
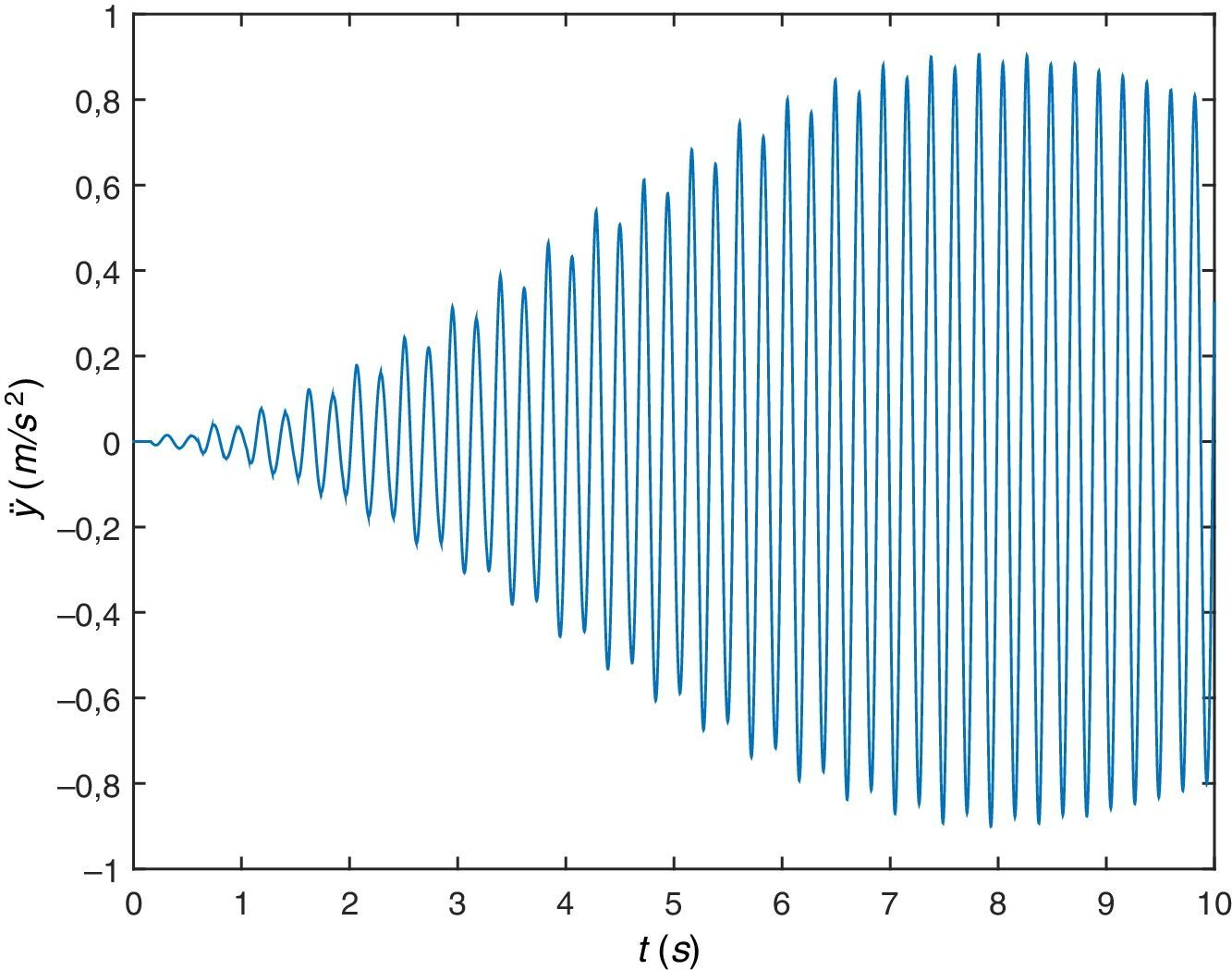
Se representa gráficamente el desplazamiento vertical (figura 14) y la aceleración vertical del COM (figura 15). En cuanto al desplazamiento se comprueba que describe una curva del tipo esperado aunque ya no es exactamente una cicloide y los valores máximos siguen siendo de aproximadamente 5cm mientras que las aceleraciones ascienden a niveles de aproximadamente 12m/s2, valores superiores a los que experimenta la sección central de la viga.
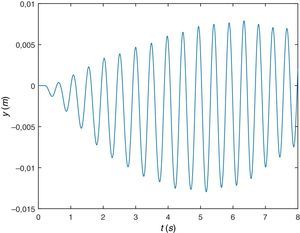
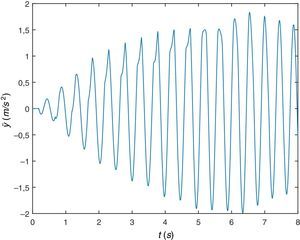
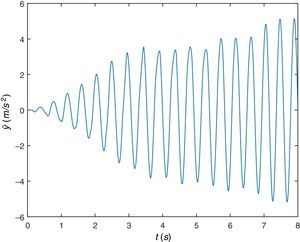
Y por último, se va a simular el peatón caminando sobre la misma viga pero a una frecuencia algo mayor, concretamente a una frecuencia de paso fp=2.4Hz. De la respuesta dinámica de la viga en desplazamientos o aceleraciones (figuras 16 y 17), se comprueba que tiene lugar el fenómeno de resonancia. En este caso la respuesta es similar al caso anterior de fp=2.0Hz, lo que hace pensar en un rango de frecuencias próximo a la frecuencia fundamental de la viga para las que se observa el fenómeno de resonancia.
4ConclusionesLa primera conclusión que se extrae del presente trabajo es la constatación de que un peatón al caminar por una estructura flexible interactúa de forma dinámica con el sistema sobre el que circula y dicha interacción afecta a ambos sistemas, peatón y estructura, como puede comprobarse en la variación de las fuerzas de contacto (GRFs) a medida que la estructura pasa de suficientemente rígida a flexible.
Una observación importante es el hecho de que la estructura presenta un valor de respuesta importante (es decir, valores elevados de desplazamientos, velocidades y aceleraciones) no sólo cuando el peatón circula a velocidad que corresponde con la frecuencia de resonancia de la estructura si no para valores relativamente cercanos a dicha frecuencia. Por lo tanto, es de esperar que para valores próximos a la frecuencia de resonancia ya se estén superando los valores de aceleraciones recomendados por la mayoría de normativas y guías técnicas.
Además, otra apreciación importante es el hecho de que en la práctica se comprueba el estado último de servicio de vibraciones midiendo la máxima respuesta en aceleraciones de la estructura. Sin embargo, en este trabajo se verifica que las aceleraciones que experimenta el peatón son siempre mayores, con lo cual al aplicar los criterios recomendados podemos no asegurar el confort de los peatones usuarios de la estructura.
Este trabajo ha sido realizado en parte con la financiación aportada al proyecto de investigación BIA2011-28493-C02-02 por el programa de apoyo a Proyectos de Investigación Fundamental No Orientada del Ministerio de Ciencia e Innovación.