META-ANALYSIS OF ASPIRIN FOR THE PREVENTION OF PREECLAMPSIA: DO THE MAIN RANDOMIZED CONTROLLED TRIALS SUPPORT AN ASSOCIATION BETWEEN LOW-DOSE ASPIRIN AND A REDUCED RISK OF DEVELOPING PREECLAMPSIA?

The meta-analysis by Ruano et al¹ evaluating 17 randomized controlled trials considering the pooled relative risk (RR) of 16,898 women at high-risk of preeclampsia receiving acetylsalicylic acid (8679 treatment and 8219 placebo) suggested that low-dose aspirin (50-150 mg/day) has a small but significant protective effect on the risk of preeclampsia: Pooled RR = 0.87; 95% confidence intervals (CI) = 0.79 to 0.96, P = 0.004). This conclusion relies uniquely on the estimate from the fixed-effects model using the Mantel-Haenszel method (MH).² However, we would like to raise some issues that allow different interpretations from the same meta-analysis.

First, results of a meta-analysis are model-dependent.³ There are potential differences between models in meta-analysis, since they have distinct properties and assumptions,^2,4 and can model for different effects.³ Second, because the choice between fixed- and random-effect models remains a controversial issue,⁵ results from both models should be considered when drawing conclusions from a meta-analysis,⁶ especially in cases where heterogeneity among treatment effects is observed.⁷ Third, when evidence for publication bias is not properly considered, results from meta-analytic studies can be seriously overestimated, yielding misleading conclusions.⁸

In this regard, we extended further the analysis by Ruano et al¹ and provide an alternative interpretation from the same data set, illustrating practical consequences of fitting different types of statistical modeling in meta-analysis. Furthermore, we illustrate that changes in model selection substantially affect the outcome of a meta-analysis, particularly when the null hypothesis of homogeneity among treatment effects is rejected.

It is well established that in the fixed-effects model, the true treatment difference is often considered to be the same for all trials.² In other words, fixed-effects models assume homogeneity among study estimates, whereas the variance of each trial estimate is based uniquely on sampling variation within the trial (within-study variance). In the random-effects model, however, the true treatment difference in each trial is itself assumed to be a random variable with a normal distribution.⁴ In addition, a second component of the total variance, the variance between-study, is estimated. Thus, in the random-effects model both within-study and between-study variances are taken into account in the assessment of the uncertainty (confidence intervals). While estimates based on fixed-effect models are specific to the particular trials included in the meta-analysis, results of the random-effects models are more amenable to generalization in terms of population.⁶ When there is no heterogeneity between trials, both models tend to provide the same overall estimate and standard error.⁵ However, this is not true when heterogeneity is present.⁵ As the heterogeneity increases, the standard error of the common estimate from the random effects model becomes wider than that from the fixed-effects model.⁴ Thus, the difference between the overall estimates from the two approaches depends strongly on the amount of between-study variation among trials.⁶ Such properties have led some authors to recommend the incorporation of the between-study variance through an implementation of the random-effects model in meta-analysis when heterogeneity is observed.⁹ In fact, published evidence suggests the broad use of random-effects models for the combination of both homogeneous and mild heterogeneous trials,⁷ whereas the combination of highly heterogeneous studies should be avoided.⁶

Hence, although Ruano et al¹ correctly tested the heterogeneity among effect sizes of individual studies, they have not considered adequately this finding. According to these authors, the homogeneity among treatment effects was formally assessed through the Cochran's Q statistic,⁴ which is a weighted sum of squares of the deviations of individual study RR estimates from the overall estimate. This statistic estimates the probability that the observed pattern of results may have occurred simply by chance. When the RRs are homogeneous, the Q statitic follows a chi-squared distribution with r - 1 degrees of freedom (df), where r is the number of studies. Unfortunately, heterogeneity tests in meta-analysis lack power, and statistical significance set at 10% is advocated.^7,10 Running Ruano et al¹ analysis again, we observed a significant evidence for heterogeneity both in the asymptotic (χ² = 25.86, df = 16, P = 0.056) and the parametric bootstrap version (1000 replications, P = 0.049) of the Q statistic. To further explore heterogeneity, we derived the proportion of the total variance of the pooled effect measure⁷ (R_i statistic) due to between-study variance (random-effects model), and quantified the I² metric,¹¹ which takes values between 0% and 100%, with higher values denoting greater degree of heterogeneity. Derivation of the R statistic suggests that almost half (46%) of the total variance from the meta-analysis of Ruano et al.¹ came from between-study variance. In × addition, the I² metric detonates the presence of moderate heterogeneity (38.1%). Thus, we provide compelling evidence for a mild to moderate heterogeneity among study results, suggesting that the conclusion of Ruano et al¹ should not be based uniquely on a fixed-effects model. In this respect, we applied to the same data set a random-effects model using the DerSimonian-Laird method (DL).⁴ Surprisingly, we found no convincing evidence for a protective effect of low-dose aspirin under this model at 5% (DL Common RR = 0.835; 95% CI = 0.697 to 1.001, P = 0.051). In order to scrutinize the heterogeneity, we fitted a random-effects regression model (meta-regression) of the log RR.¹² This regression model investigates whether any study feature influences the magnitude of the relative risk in individual studies. Year of publication, impact factor (according to the Journal of Citation Reports 2004), aspirin dose, sample size, and gestation age of inclusion were assigned as study-level covariates. An exploratory stepwise backward random-effects meta-regression reveals that year of publication and total sample size were associated with reduced magnitudes of RR (year of publication slope coefficient = 0.07; 95% CI = 0.03 to 0.11, P < 0.001 and total sample size slope coefficient = 4 × 10⁻⁵; 95% CI = 6.9 10⁻⁶ to 7 × 10⁻⁵, P = 0.02). These meta-regression coefficients are estimates of the expected increment in the log RR per unit increase in the covariate. In other words, in the studies of low-dose aspirin for prevention of preeclampsia (high-risk women) the log RR is estimated to rise 0.07 per year increase and to increase = 4 10⁻⁵ per individual added in each the study. These findings led us to a perform sensitivity analysis considering total sample size.¹³ In this analysis we separately explored studies with sample size >1000 and <=1000. By combining RR from these 14 small trials (1549 treatment and 1704 placebo) with sample sizes equal or smaller than 1000 subjects, we obtained a marginally significant but stronger protective effect of low-dose aspirin in the prevention of preeclampsia (DL common RR = 0.67; 95% CI = 0.48 to 0.93, P = 0.02, Q statistic, χ² = 23.15, df = 13, P = 0.04). In contrast, by combining the 3 larger studies totaling 13645 individuals (7130 treatment and 6515 placebo) we found no evidence for a role of low-dose aspirin in preeclampsia prevention (MH common RR = 0.91; 95% CI = 0.82 to 1.02, P = 0.094, Q statistic parametric bootstrap version with 1000 replications, P = 0.34). Likewise, stratification of studies by samples sizes >500 and <=500 yielded virtually the same results.

Disagreements between large and smaller trials are compatible with the presence of publication bias,⁸ a tendency on the part of investigators, editors, and reviewers to publish preferentially studies with positive results (“statistically significant results”).^6,8,14 In fact, it is well recognized that earlier trials tend to have smaller samples, less methodological quality, and to give more impressive estimates of treatment effect than subsequent research.¹³ However, publication bias may lead to overestimation of treatment effects in meta-analysis, since negative, nonstatistically-significant small trials are less likely to be published.⁸ Therefore, we tested graphically and formally the presence of publication bias in this set of 14 studies. We carried out analysis of publication bias using the Egger's regression asymmetry statistics⁸ and the Begg-Mazumdar adjusted rank correlation test.¹⁵ In addition, funnel plot asymmetry was also used.^6,8 The funnel plot is based on the fact that precision in estimating the underlying treatment effect will increase as the sample size of the included trials increases.⁶ Results from small studies will scatter widely at the bottom of the graph, with the spread narrowing among larger studies.⁸ In the absence of bias, the plot will resemble a symmetrical inverted funnel. Conversely, if negative small trials are less likely to be published, the graph will tend to be skewed (asymmetric).⁶

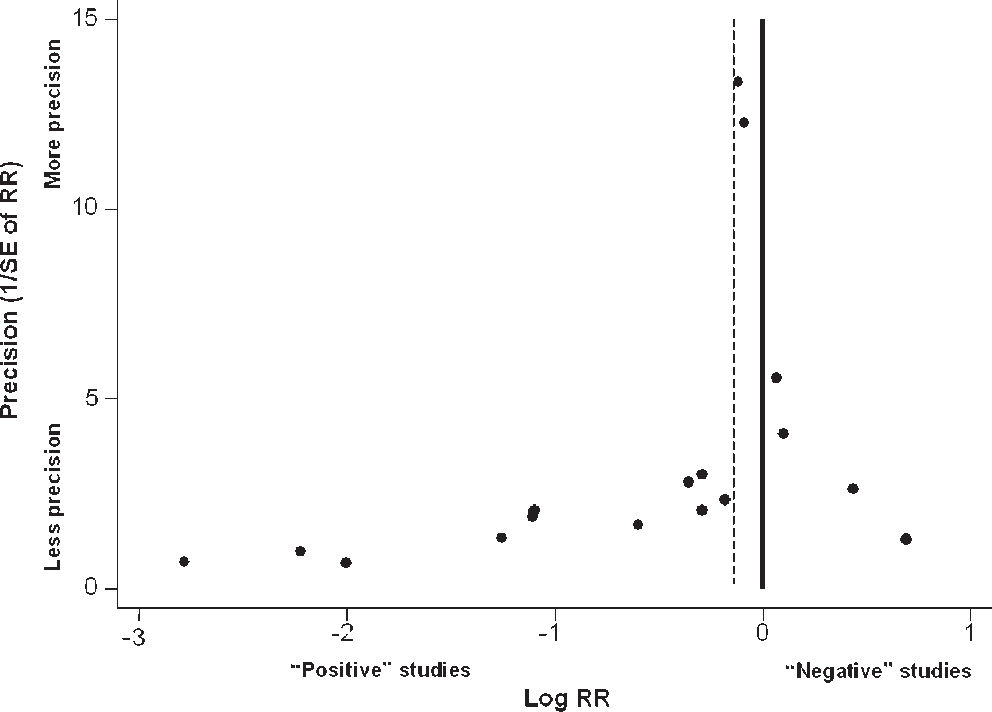
Although heterogeneity may affect these statistics,^8,16 both tests showed reasonable evidence for publication bias in the set of 14 small studies (Begg-Mazumdar's test, P = 0.02; Egger's statistics, P = 0.001). Additionally, as depicted in Figure 1, the visual inspection of the funnel plot comparing precision (1/Standard Error of RR) against treatment effect (Log RR) reveals noticeable asymmetry (all 17 trials included), reinforcing the probable presence of publication bias.

Figure 1.

Funnel plot of 17 studies investigating the effect of low-dose aspirin for preeclampsia prevention (high-risk women) previously analyzed by Ruano et al.¹ Vertical axis depicts the precision represented here by the inverse of the standard error (SE) of relative risk (RR). Horizontal axis represents the logarithm of RR. Solid line denotes null effect and dotted line is the pooled RR under a fixed-effects model (Mantel-Haenszel method). “Positive” studies denote trials showing a protective effect of aspirin in the prevention of preeclampsia (high-risk women), but not necessarily reflecting “statistically significant” studies. “Negative” studies represent trials showing no beneficial effects of aspirin in preeclampsia (high-risk women). Visual inspection of the funnel plot suggests asymmetry. At the bottom right: are small trials showing no beneficial effects missing?

These results do not completely rule out a role for aspirin in the preeclampsia prevention. However, taken together, the presence of heterogeneity, the conflicting results between large and smaller trials, the lack of robustness between fixed- and random-effects models, and the putative presence of publication bias call into question the reliability of the evidence for a protective effect of low-dose aspirin on the risk of preeclampsia.

In conclusion, despite the 20 years of research since the first report, the relationship between aspirin treatment and a reduced risk of preeclampsia in women considered at high-risk still remains an unresolved issue. Further approaches, such as meta-analysis considering language bias or individual patient data meta-analysis,¹⁷ are required.