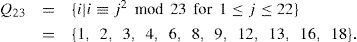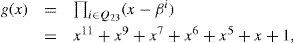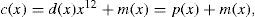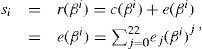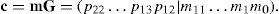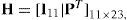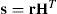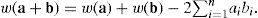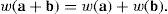High-Speed Decoding of the Binary Golay Code

Abstract

Recently, some table-lookup decoding algorithms (TLDAs) have been used to correct the binary Golay code. This paper proposes an efficient high-speed TLDA called message-syndrome decoding algorithm (MSDA) by using the message syndrome to correct the binary systematic Golay code. The proposed MSDA is based on the novel message-syndrome lookup table (MSLT). The MSLT merely consists of 12 candidate syndromes and its memory size is significantly smaller than other existing lookup tables. Computer software simulation results show that the decoding speed of the proposed MSDA is superior to other proposed TLDAs.

1

Introduction

The well-known binary Golay code, also called the binary (23, 12, 7) quadratic residue (QR) code [2], was first discovered by Golay [1] in 1949. It is a very useful perfect linear error-correcting code; particularly, it has been used in the past decades for a variety of applications involving a parity bit being added to each word to yield a half-rate code called the binary (24, 12, 8) extended Golay code. One of its most interesting applications is the provision of error control in the Voyager missions [2]. The Golay code can allow the correction of up to t=⌊(d-1)/2⌋=⌊(7-1)/2⌋=3 errors, where ⌊x⌋ denotes the greatest integer less than or equal to x, t is the error-correcting capability, and d is the minimum Hamming distance of the code.

In the past few decades, several decoding techniques have been developed to decode the binary Golay codes, for example, the famous algebraic decoding algorithm (ADA) developed by Elia [3], the notable shift-search algorithm proposed by Reed et al. [4] after that, and the inverse-free Berlekamp–Massey algorithm used to obtain the error-locator polynomial by Chen et al. [5]. The above is some representative literature on ADAs used to correct Golay codes.

Recently, the TLDAs given in [6-9] have acquired a prominent role in error-correcting decoding. A TLDA with a refined lookup table (RLT) has been proposed by Lin et al. [8]; the RLT only needs 168 bytes memory size. The memory size of the RLT is the smallest memory size required to correct the Golay code until now. In general, the TLDA makes considerably faster decoding speeds possible for the cyclic codes, in comparison with the ADA. However, the TLDA requires an extra memory space in the decoder chip or software and it increases the decoding cost rapidly when the code length is large. Although the ADA does not need any lookup table, it requires a large number of complicated computations in the finite field. These complicated computations will degrade the decoding performance and lead to a serious decoding delay as the code length increases [10].

Chen et al. [7] proposed the fast lookup table decoding algorithm (FLTDA) with a lookup table of 1.35K bytes by using the shift-search algorithm [4] to decode the Golay code. The famous syndrome decoding algorithm (SDA) with a reduced-size lookup table (RSLT) given in [2, p119] requires 89 syndromes and their corresponding error patterns, whereas the RSLT requires 445 bytes of memory.

Lin et al. [8] proposed the syndrome-weight decoding algorithm (SWDA) with RLT which needs 168 bytes of memory, and the simulation result shows that the decoding speed is approximately 9.7 times faster than the improved Elia’s decoding algorithm (EDA).

In this paper, an efficient high-speed MSDA with a MSLT is proposed to decode the binary systematic Golay code. The novel MSLT consists only of 12 candidate syndromes which have one error in the message part of the received vector, and it merely requires 24 bytes of memory. Software simulation results show that the average decoding speed is the fastest among the TLDAs as mentioned above. In the four-error soft-decision decoder in [11], the improved EDA is the role of the hard-decision decoder. We substituted the proposed MSDA for the improved EDA in the four-error soft-decision decoder. Apparently, the decoding speed of the soft-decision decoder was faster than before.

The remainder of this paper is organized as follows: The background of the binary systematic Golay code is briefly reviewed in Section 2. Some related TLDAs and related theorems are briefly introduced in Section 3. The proposed MSDA is presented in Section 4. Computer simulation results are given in Section 5. Finally, this paper concludes with a brief summary in Section 6.

2

Background of the binary systematic Golay code

The binary (23, 12, 7) Golay code can be defined as a linear cyclic code or QR code [2]. For the binary Golay code over finite field GF(2¹¹), its quadratic residue set is given by

The generator polynomial g(x) of the binary Golay code is defined by

where β is a primitive 23rd root of unity in GF(2¹¹). Let the codeword polynomial C(x)=∑i=0n-1Cixi, where C_i ∈ GF(2) for 0 ≤ i ≤ 22, and the message polynomial m(x)=∑i=0k-1mixi, where k = 12 is the message length and m_i ∈ GF(2) for 0 ≤ i ≤ 11. C(x) is a multiple of g(x), namely, C(x) = m(x)g(x). Also, let the product m(x)x¹¹ divide by g(x), then one has m(x)x¹¹ = q(x)g(x) + d(x). Multiplying both sides of last expression by x¹² and using x²³ = 1, one yields d(x)x¹² + m(x) = (q(x)x¹²)g(x). The term (d(x)x¹² + m(x)), which is a multiple of g(x), is a systematic codeword given by

where p(x)=∑i=1222pixi denotes the parity-check polynomial [12] of a codeword and p_i ∈ GF(2) for 12 ≤ i ≤ 22.

The binary systematic Golay code is practically applied in the standard of the communication system for automatic link establishment (ALE) by the United States Department of Defense [13]. Now, let a 12-bit message be encoded into a 23-bit systematic codeword and be transmitted through a noisy channel to obtain a received word of the form r(x) = c(x) + e(x). e(x)=∑i=022eixi is the error pattern polynomial, where e_i ∈ GF(2) for 0 ≤ i ≤ 22. The syndromes of the code are defined by

where i ∈ Q₂₃.

To simplify the polynomial expressions above, the message, codeword, error pattern, received word, and syndrome polynomials can be expressed as the binary vector forms m = (m₁₁... m₁m₀), c = (c₂₂... c₁c₀), e = (e₂₂... e₁e₀), r = c + e = (r₂₂... r₁r₀), and s = (s₁₀... s₁s₀), respectively. For the binary systematic Golay code, it follows from [2, p85] that the systematic generator matrix G can be expressed as follows:

where P and I₁₂ denote the 12×11 matrix and the 12×12 identity matrix, respectively. The systematic vector form of the codeword can be obtained by

The parity-check polynomial h(x) = x¹² + x¹⁰ + x⁷ + x⁴ + x³ + x² + x + 1 is a factor of x²³ – 1. The 11×23 parity-check matrix H can be expressed as follows:

where PT is a 11×12 transpose matrix of P and I₁₁ is a 11×11 identity matrix.

The HT denotes the 23 × 11 transpose matrix of H; that is, HT=[I11P]23×11. The vector form of the syndrome can be defined by

The following lemma given in [14] shows that the mapping between the syndromes and error patterns under the error-correcting capability is one-to-one.

Lemma 1.

The mapping between the syndromes of a code and the corresponding error patterns of weight ≤ t is one-to-one.

3

Related work and theorems

In this section, some related TLDAs and theorems are briefly introduced in order to develop the proposed MSDA. For the TLDA, the following definition, theorems and corollary given in [9] are needed.

Definition 1.

Let the Hamming norm or weight of a binary vector a = (a_n-1... a₁a₀) be designated by w(a). The Hamming distance between two binary vectors a and b is defined by d(a, b) = w(a + b).

Theorem 1.

Let a = (a_n-1... a₁a₀) and b = (b_n-1... b₁b₀) be two binary vectors, then

Corollary 1.

Let a and b, defined in Definition 1, be two binary vectors. If a_ib_i = 0 for 1 ≤ i ≤ n, then

Theorem 2.

For the binary systematic (n, k, d) QR codes, let us assume that there are v errors in the received word, where 1 ≤ v ≤ t. All v errors occur in the n – k parity-check bits if and only if the weight of syndrome w(s) = v.

As mentioned above, the error-correcting capability of the binary Golay code is t =3. The full lookup table (FLT) in the conventional table lookup decoding algorithm (CTLDA) requires ∑i=1323i=2,047 syndromes and their corresponding error patterns by Lemma 1. Each syndrome and error pattern needs 2 bytes and 3 bytes, respectively, to store in the FLT. Thus, the total memory size needed for the FLT is (2047 × (2 + 3)) = 10,235 bytes. However, such a large memory is less efficient in practice.

Recently, some useful TLDAs have been presented in the literature to reduce the memory size of the FLT. The LTDA [7] used the shift-search method [4] to reduce the memory size of the FLT and the binary-search method to reduce the search time in the FLT. The shift-search method deletes all v = t error patterns and keeps 1 ≤ v ≤ t – 1 error patterns.

Therefore, the LTDA needs ∑i=1t-123i=∑i=1223i=276 syndromes and their corresponding error patterns; that is, the FLT needs 276 × (2 + 3) = 1,380 bytes memory size. Nevertheless, the memory size of the FLT is still large and the simulation result shows that the average decoding time of the proposed MSDA is about 10.6 times faster that the LTDA. To develop the following TLDAs, Theorem 3 is useful to reduce the memory size of the FLT. The well-known SDA with RSLT [2, p119] has the following useful theorem of the cyclic codes to dramatically reduce the memory size of the FLT. For more detailed proof of this theorem, see [2, p118].

Theorem 3.

Let s(x) be the syndrome polynomial corresponding to a received polynomial r(x). Also, let r⁽¹⁾(x) be the polynomial obtained by cyclically shifting the coefficients of r(x) one bit to the left. Then the remainder obtained when dividing xs(x) by g(x) is the syndrome s⁽¹⁾(x) corresponding to r⁽¹⁾(x).

Decoding the binary systematic Golay code by Theorem 3, the RSLT of the SDA only needs 1/23 memory size of the FLT, namely 10,235/23 = 445 bytes memory size [8]. Nonetheless, the memory size of the RSLT is still large and can be further reduced. Similarly, by Theorem 3, r⁽j⁾(x) is the polynomial obtained by cyclically shifting the coefficients of r(x) j bits to the left. Next, the syndrome difference s_di is defined by s_di = s – s_i for 1 ≤ i ≤ N, where s is the syndrome of r, s_i is the syndrome in lookup table, and N is the table size. Similarly, the syndrome difference sdi(j) is defined by sdi(j)=s(j)-si for 1 ≤ j ≤ n, where s⁽j⁾ is the syndrome of r⁽j⁾. By using the property of the syndrome difference, the RLT of the SWDA only requires 168 bytes. However, the decoding speed is not very outstanding according to the simulation result. To overcome this problem, the MSDA is presented by using the syndrome that only one error occurred in the message part of the received word.

4

MSDA for the binary Golay code

In this section, an efficient high-speed MSDA with a MSLT for decoding the binary systematic Golay code is developed to further reduce the decoding time and the memory size of the RLT. By Theorem 2 and (8), it is obvious that at least one error is in the message bits if the weight of syndrome w(s) > 3.

Definition 2.

The message-syndrome lookup table (MSLT) is a table of all the error patterns occurred in the message part with weight 1≤v≤⌊t/2⌋ together with their corresponding syndromes, where ⌊x⌋ denotes the smallest integer less than or equal to x.

Therefore, the novel MSLT merely consists of 12 candidate syndromes which are the syndromes of having one error in the message part; that is, s_i is the syndrome of e_i which is one error located at bit i for 1 ≤ i ≤ 12. The MSLT is listed in Table 1.

Table 1.

MSLT for the Binary Systematic Golay Code.

Syndrome	Syndrome
s1= (01011100011)	s2= (10111000110)
s3= (00101101111)	s4= (01011011110)
s5= (10110111100)	s6= (00110011011)
s7= (01100110110)	s8= (11001101100)
s9= (11000111011)	s10= (11010010101)
s11= (11111001001)	s12= (10101110001)

To develop the proposed MSDA by using the MSLT, the following lemma and properties are necessary.

Lemma 2.

For the binary Golay code, let e be an error pattern, and let e_p and e_m be its parity-check part and message part, respectively. Let s_p and s_m be the syndromes corresponding to e_p and e_m, respectively. Assume that w(e) ≤ 3, then we have

• (i)

  w(s_p) = w(e_p);

• (ii)

  w(s_m) ≥d –w(e_m), whered = 7;

• (iii)

  ((s_m << 12) + e_m) is always a codeword, where “<<“ denotes the logical left shift operator in programming or the extension by zeros on the right in mathematics.

Proof: By Equation (8), (i) is obvious. Again, by Equation (8), given that ((sm<<12)+em)HT=((sm<<12)+em)[l11P]=(sm<<12)[l11P]+em[l11P]=sm+sm=0, ((s_m << 12)+ e_m) is thus a codeword, which proves (iii). Hence, w((s_m << 12) + e_m) = w(s_m) + w(e_m) ≥ d, that is, w(s_m) ≥ d – w(e_m). The proof is thus completed.

By Lemma 2, if v ≤ t, then one can obtain the following two properties.

Property 1.

For the binary Golay code, the weight of the syndrome difference w(s_di) has the following cases:

Case 1:	If w(s) ≤ 3, then all three errors are in the parity-check part and no error is in the message part.
Case 2:	If w(s) > 3 and w(sdi) < 3, then only 1 error is in the message part.
Case 3:	If w(s) > 3 and w(sdi) > 3, than at least 2 errors are in the message part.

Next, for Case 3 of Property 1, the r and s are cyclically shifted left by 11 bits, then one obtains r⁽¹¹⁾ and s⁽¹¹⁾, respectively. Thus, one yields the following property.

Property 2

For the binary Golay code, if w(s) > 3 and w(s_di) > 3, then the weight of s⁽¹¹⁾ and sdi(11) have the following cases:

Case 1:	If w(s^(11)) = 2 or 3, then r has at least 2 errors in the message part and no error is in the parity-check part.
Case 2:	If w(s^(11)) > 3 and w(sdi(11))≤2, then r has at least 2 errors in the message part.
Case 3:	If w(s^(11)) > 3 or w(sdi(11))>3, then 2 errors are in the message part and one of them is at the position of bit 0.

By using the MSLT, the decoding process of the MSDA is as follows:

• (1)

  Giving a received vectorr.

• (2)

  Compute the syndromes = rHT and its weightw(s).

• (3)

  Ifw(s) ≤ 3, then returnc = r – (s << 12), and go to step 13.

• (4)

  For 1 ≤ i ≤ 12, compute the syndromes_di = s –s_i and its weightw(s_di).

• (5)

  Ifw(s_di) ≤ 2, then returnc = r – (s_di << 12) – (1 << (i – 1)), and go to step 13.

• (6)

  Cyclically shiftr ands left by 11 bits obtainingr⁽¹¹⁾ ands⁽¹¹⁾, and then computew(s⁽¹¹⁾).

• (7)

  Ifw(s⁽¹¹⁾) = 2 or 3, then returnc = ((r⁽¹¹⁾ – (s⁽¹¹⁾ << 12)) << 12) – ((r⁽¹¹⁾ – (s⁽¹¹⁾ << 12)) >> 11), and go to step 13.

• (8)

  For 1 ≤ i ≤ 12, compute the syndrome sdi(11)=s(11)-si and its weight w(sdi(11)).

• (9)

  If w(sdi(11)) or 2, then return c=((r(11)-(sdi(11)<<12)-(1<<(i-1)))<<12)-((r(11)-(sdi(11)<<12)-(1<<(i-1)))>>11), and go to step 13.

• (10)

  Computer’ = r – 1 ands’ = s –s₁.

• (11)

  For 2 ≤ i ≤ 12, compute the syndromes’_di = s’ –s_i and its weightw(s’_di).

• (12)

  Ifw(s’_di) = 1, then returnc = r’ – (s’_di << 12) – (1 << (i – 1)).

• (13)

  Stop.

An example is given below. By (6), a message vector m = (100000000000) is encoded into a binary systematic Golay code c = (10101110001100000000000). Assume that a noise vector is e = (00010000000000010000001), then the received word becomes r = c + e = (10111110001100010000001). The decoding steps proceed as follows:

• (1)

  The received vector isr = (10111110001100010000001).

• (2)

  Compute the syndromes = (10000001111) and its weightw(s) = 5.

• (3)

  Given thatw(s) > 3, go to step 4.

• (4)

  Fori = 1, compute the syndromes_d1 = s –s₁ = (11011101100) and its weightw(s_d1) = 7.

• (5)

  Given thatw(s_d1) > 2, go to step 4. …repeating steps 4 and 5…

• (4)

  Fori = 12, compute the syndromes_d12 = s –s₁₂ = (00101111110) and its weightw(s_d12) = 7.

• (5)

  Given thatw(s_d12) > 2, go to step 6.

• (6)

  Cyclically shiftr ands left by 11 bits obtainingr⁽¹¹⁾ = (10001000000110111110001) ands⁽¹¹⁾ = (01101011101), and then computew(s⁽¹¹⁾) = 7.

• (7)

  Given thatw(s⁽¹¹⁾) ≠ 2 or 3, go to step 8.

• (8)

  Fori = 1, compute the syndrome sd1(11)=s(11)-s1=(00110111110) and its weight w(sd1(11))=7.

• (9)

  Given that w(sd1(11))>2, go to step 8.…repeating steps 8 and 9…

• (8)

  Fori = 12, compute the syndrome sd12(11)=s(11)-s12=(1100010100) and its weight w(sd12(11))=5.

• (9)

  Given that w(sd12(11))>2, go to step 10.

• (10)

  Computer’ = r – 1 = (10111110001100010000000) ands’ = s – s1 = (11011101100).

• (11)

  Fori = 2, compute the syndromes’_d>2 = s’ –s₂ = (01100101010) and its weightw(s’_d2) = 5.

• (12)

  Given thatw(s’_d2) > 1, go to step 11. …repeating steps 11 and 12…

• (13)

  Fori = 8, compute the syndromes’_d8 = s’ –s₈ = (00010000000) and its weightw(s’_d8) = 1.

• (14)

  Ifw(s’_d8) = 1, then return the correct codewordc = r1 – (s’_d8 << 12) – (1 << (i – 1)) = (10111110001100010000000) – (00010000000000000000000) – (10000000) = (10101110001100000000000). Go to step 13.

• (15)

  Stop.

Therefore, the correct message can be retrieved from the received vector.

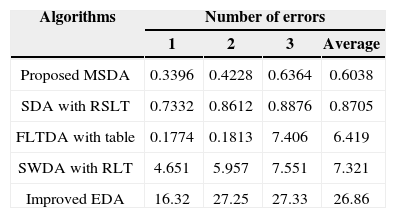
5

Simulation results

The proposed MSDA has been programmed in C++ language. On an Intel Q6600 PC, all codewords with up to three errors, namely 212×∑i=13Ci23=8,384512 received vectors, were created to check every possible error pattern. The detailed decoding times for decoding the binary systematic Golay code with different decoding algorithms are given in Table 2. The proposed MSDA has the fastest average decoding time and works perfectly with an average decoding time of 0.6038 μs per error pattern.

Table 2.

Computer Decoding Time for Decoding the Binary Golay Code (in μs).

Algorithms	Number of errors
	1	2	3	Average
Proposed MSDA	0.3396	0.4228	0.6364	0.6038
SDA with RSLT	0.7332	0.8612	0.8876	0.8705
FLTDA with table	0.1774	0.1813	7.406	6.419
SWDA with RLT	4.651	5.957	7.551	7.321
Improved EDA	16.32	27.25	27.33	26.86

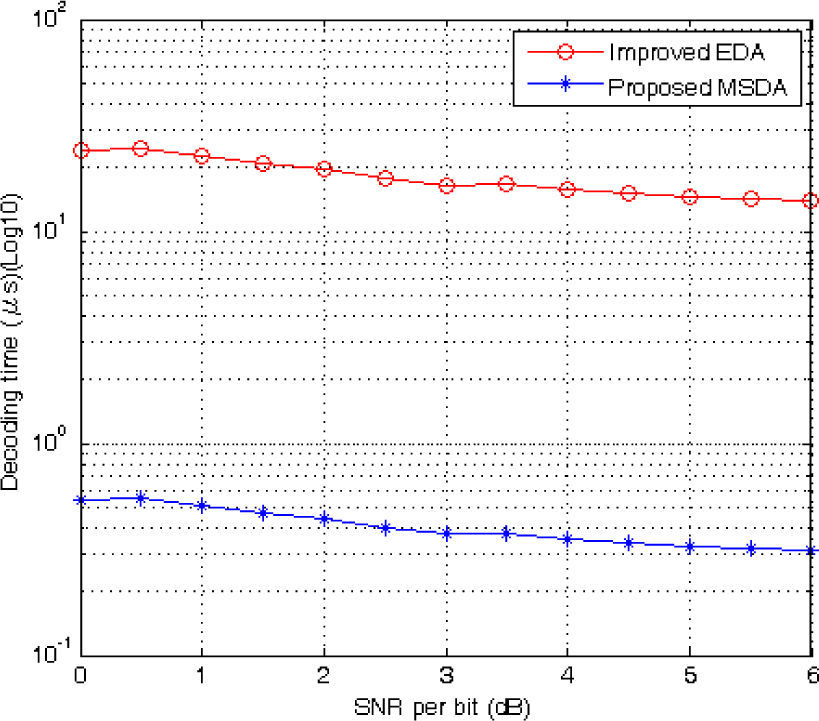
From Table 2, the proposed MSDA has the fastest average decoding time and is about 44.5 times faster than the improved EDA. Furthermore, we substituted the proposed MSDA for the improved EDA in the four-error soft-decision decoder [11]. Apparently, the decoding speed of the soft-decision decoder was about 44.5 times faster than before. The decoding time of the two hard-decision decoders with respect to the SNR values is shown in Figure 1.

Figure 1.

Decoding Time of Two Hard-Decision Decoders at SNR of 0~6 dB.

6

Conclusions

This paper presented a simple and more efficient decoding algorithm for decoding the binary systematic Golay code. The key ideas of the MSDA are based on the properties of cyclic codes, the one-error syndrome in the message part, the weight of syndrome, the weight of syndrome difference, Property 1, and Property 2. The MSLT of the MSDA merely requires a very small memory size of 24 bytes. These facts lead to a substantial improvement in decoding the binary systematic Golay code. Simulation results show that, following the new decoding strategies, the proposed MSDA achieves the best efficiency. Hence, it is naturally suitable and proper for DSP or embedded system software implementation.