La resolución de problemas desempeña un papel de gran relevancia tanto en la educación matemática como en el aprendizaje de las demás disciplinas científicas. El objetivo de esta investigación es analizar las diferentes estrategias de resolución de problemas algebraicos en función del sexo. Para tal fin, se han estudiado las formas de resolver problemas de 598 estudiantes de 2.°, 3.° y 4.° de Educación Secundaria Obligatoria. El alumnado se clasifica en 3 grupos de resolución, en función de los procedimientos empleados en la resolución de los problemas: el grupo de resolución algebraico, el grupo mixto (emplean el álgebra y la aritmética) y el grupo no definido (procedimiento ni algebraico ni aritmético). Los datos obtenidos indican que no se encuentran diferencias estadísticamente significativas entre chicos y chicas en cuanto a procedimientos de resolución. Se discuten las implicaciones cognitivas, educativas y sociales de los resultados.
Problem solving plays a very important role in both mathematics education and in the learning of other scientific disciplines. The objective of this study is to analyze the different strategies used to solve mathematical problems according to sex. To do this, the ways 598 students in 8th, 9th and 10th grade of Secondary School solved problems were studied. The students were classified into 3 groups, according to the different problem solving procedures: the algebra problem solving group, the mixed group (algebraic and arithmetic solving) and the undefined group (neither algebraic nor arithmetic). The data showed that there were no statistically significant differences between boys and girls in terms of solving processes. The cognitive, educational and social implications are discussed.
La resolución de problemas va más allá del aprendizaje de las matemáticas, ya que adquirir competencia en dichos procedimientos es de gran ayuda en cualquier disciplina científica (Lorenzo, 2005). En la actual sociedad de la información, el aprendizaje de las matemáticas se asocia con la resolución de situaciones complejas y las competencias conceptuales que requieren habilidad verbal del alumnado (Sciarra y Seirup, 2008). Dichas destrezas, principalmente adquiridas gracias al dominio de la resolución de problemas, fomentan el razonamiento verbal y constituyen la base de multitud de currículos y programas de estudios de matemáticas a lo largo del mundo.
La cuestión de la resolución de problemas aritmético-algebraicos ha sido estudiada en relación con el cambio cognitivo que supone para el alumnado la transición de la aritmética al álgebra (Bednarz y Janvier, 1996; Filloy, Rojano y Rubio, 2001; Puig y Cerdán, 1990a; Stacey y MacGregor, 2000). Se han explorado los problemas con el fin de hacer frente a la dificultad de especificar las diferencias entre los problemas aritméticos y los algebraicos. En este contexto, se ha discutido si es posible realizar una clasificación dicotómica de este tipo, debido a que los elementos que componen un problema verbal son aparentemente insuficientes para su caracterización; es más plausible pensar que sea la relación de dichos elementos con las estrategias de resolución puestas en juego la que defina la naturaleza aritmética o algebraica de los problemas.
Ciertos estudios se centran en la naturaleza de los problemas verbales, analizando los procesos de traducción del problema del lenguaje natural a la expresión matemática (Puig y Cerdán, 1990a; Puig y Cerdán, 1990b). Así, si el proceso de traducción conduce a una expresión que solo contiene valores conocidos, la resolución se considerará aritmética. Por el contrario, si la expresión deriva en uno o más valores desconocidos, la resolución será de naturaleza algebraica; dichos procesos de traducción dan lugar al método de análisis-síntesis y al método cartesiano (Cerdán, 2008; Puig y Cerdán, 1990a).
Los cambios profundos que acarrea el aprendizaje del álgebra en los hábitos aritméticos no tienen lugar de forma espontánea en el alumnado. La intervención de la enseñanza, en ese momento de transición de la fase aritmética al conocimiento algebraico, puede ser crucial para la mayoría del estudiantado que comienza el aprendizaje del álgebra.
En la transición de educación primaria a secundaria se han detectado 3 tipos de situaciones (Filloy, Puig y Rojano, 2008). Un tipo se refiere al síndrome de la reversibilidad de la multiplicación y consiste en no hacer uso de la reversibilidad de la multiplicación a la hora de resolver ecuaciones de tipo Ax=B. La interpretación de la x como cantidad desconocida hace que el alumnado no sepa qué hacer y que recurra al método de ensayo-error. Este método puede resultar complicado si la cantidad B es alta. Un segundo tipo es el concerniente a los diferentes usos de la noción de igualdad. Este caso se debe, principalmente, al uso operacional de la igualdad heredado de la aritmética. Esta concepción choca con la función relacional de la igualdad que caracteriza a las ecuaciones algebraicas. La tercera situación es la dificultad para traducir el enunciado del lenguaje natural al algebraico y viceversa. En este último caso se refiere al hecho de que los tipos de notación del álgebra son básicamente los mismos que los empleados en la resolución aritmética: los números, las operaciones y el signo igual, entre otros; sin embargo, su significado y su función difieren en ambas estrategias de resolución. Esto implica dificultades en la traducción del lenguaje natural del enunciado al lenguaje algebraico y viceversa.
Más generalmente, los problemas matemáticos se presentan como un excelente laboratorio natural en el que se puede estudiar, con claridad y precisión, cómo el alumnado adquiere, elabora y emplea destrezas para resolver situaciones problemáticas (Mayer, 1986).
La resolución de problemas tiene una gran relevancia educativa y evolutiva. En este sentido, se han destacado varias características: su estructura formal permite poner de relieve la forma y organización de los procesos mentales; es posible presentar problemas con soluciones definidas y exactas; se emplean algoritmos que acentúan la visibilidad de los procesos mentales; los contenidos ofrecen una estructura jerárquica más clara que en otros campos del conocimiento; y, por último, se pone de relieve que los errores en esta disciplina resultan de más fácil detección que en otras disciplinas (Rivière, 1990).
En definitiva, si se tiene en cuenta el papel destacado que tiene la resolución de problemas en la educación científica y las dificultades que su aprendizaje genera, este estudio consiste en analizar las diferentes estrategias empleadas para resolver problemas, para comprobar si se dan diferencias de sexo en dichos patrones resolutorios.
La variación en las estrategias de resolución no han sido exploradas detalladamente en función del sexo en la etapa de educación secundaria, aunque sí con relación a otros parámetros (Halpern, Wai y Saw, 2005; Nuttall, Casey y Pezaris, 2005; Rilea, Roskos-Ewoldsen y Boles, 2004). El indicador más investigado con respecto a las diferencias de sexo ha sido el aprendizaje de las matemáticas medido a través del rendimiento académico; históricamente, los chicos han destacado más que las chicas en matemáticas, considerada una disciplina masculina (Meece, Glienke y Burg, 2006; Watt, 2004). El último informe PISA 2012 (IE, 2013), que evalúa la competencia matemática en alumnado de 15 años, muestra que los alumnos obtienen mejores resultados que las alumnas en la mayoría de los estados pertenecientes a la Organización para la Cooperación y el Desarrollo Económicos (OCDE). En el Estado español, concretamente, la diferencia es mayor que la del promedio de los países de la OCDE, si bien es cierto que en algunas comunidades autónomas las variaciones no son estadísticamente significativas. Otros estudios detectan cambios en la superioridad de los varones (National Center for Education Statistics NCES, 2004).
A juzgar por lo recogido hasta el momento, el objetivo de esta investigación es analizar las formas de resolver problemas algebraicos de chicas y chicos con el fin de discutir los resultados en relación con la presunta mayor capacidad de estos últimos. Pedagógicamente, resulta importante conocer las posibles diferencias que se puedan producir para poder así plantear cambios educativos que favorezcan la igualdad de oportunidades entre sexos.
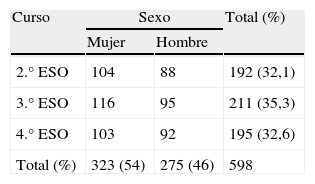
MétodoParticipantesLa muestra la componen 598 estudiantes de 2.° de Educación Secundaria Obligatoria (ESO) (8.° grado, 13-14 años), de 3.° (9.° grado, 14-15 años) y de 4.° (10.° grado, 15-16 años), de los cuales 292 eran mujeres y 242, hombres.
La recogida de datos se ha realizado en 8 centros educativos pertenecientes al País Vasco (España), de los cuales 5 eran integrantes de la red pública y 3 de la red privada concertada. Tras contactar con varios centros, finalmente se seleccionan aquellos que responden positivamente a la oferta de participación, por lo que se trata de una muestra de conveniencia.
Toma parte en la investigación todo el alumnado que se encuentra en el aula en el momento de la realización. Además, en cada centro educativo, todos los grupos de los cursos seleccionados participan en la prueba.
En la tabla 1 se muestra la distribución de la muestra en función del curso académico y del sexo.
Instrumento de medidaLos 3 problemas propuestos son introducidos por Stacey y MacGregor (2000) y van de menor a mayor complejidad en cuanto a su resolución con métodos no algebraicos. El segundo problema es análogo al primero, con la diferencia de que se piden 3 resultados en lugar de 2 (ver Anexo).
Con el objetivo de medir las estrategias llevadas a cabo en cada problema propuesto, la codificación se ordena en 4 categorías propuestas por Khng y Lee (2009): algebraica, si el planteamiento está definido por una o más incógnitas y se resuelve mediante una o más ecuaciones; aritmética, si tanto el planteamiento como la resolución se basan en una técnica aritmética, esto es, sin recurrir ni a incógnita ni a ecuación; mixta, categoría donde se ubican los problemas en los que se usa una letra en alguna parte de la resolución pero la técnica es predominantemente aritmética y, por tanto, se consideran procedimientos aritméticos; y sin estrategia/sin respuesta, donde se agrupan los métodos sin identificar o los problemas sin resolver.
A la hora de clasificar la resolución como aritmética, se han dado como válidas la resolución aritmética y la mixta.
El instrumento de medida para las estrategias de resolución de problemas aritmético-algebraicos consta de 3 problemas verbales a resolver. A cada individuo de la muestra se le agrupa en una categoría de las 3 siguientes: el grupo G3 (grupo de resolución de perfil algebraico), correspondiente a los sujetos que resuelven correctamente la totalidad de los problemas algebraicamente, o, en su defecto, resuelven 2 algebraicamente y en el tercero hacen un planteamiento algebraico (planteando las incógnitas y la ecuación), aunque no den con la solución correcta por un error de cálculo, y no procedimental; el grupo G2 (grupo de resolución de perfil mixto), compuesto por los individuos que utilizan estrategias tanto algebraicas como aritméticas, dependiendo del problema a resolver. Por tanto, se incluye en este grupo al alumnado que resuelve correctamente 2 problemas algebraicamente y uno aritméticamente, o viceversa (2 aritméticamente y uno algebraicamente); y el grupo G1 (grupo de resolución de perfil no definido), al que pertenece el alumnado que no encaja ni en G3 ni en G2, es decir, no resuelve sistemáticamente ni de modo algebraico ni de modo aritmético, ni tampoco alternando ambas técnicas. Se incluye en este conjunto a los sujetos que obtienen en algún problema (en uno, en 2, o en los 3) la clasificación de sin estrategia/sin respuesta.
El grupo G3 pertenece a los individuos que resuelven los problemas algebraicamente. El grupo G2 lo componen individuos que resuelven de manera mixta, en algunas ocasiones aritmética y en otras algebraicamente. Por último, en el grupo G1 se incluyea los sujetos que no hacen uso del álgebra o lo hacen escasamente, y tampoco dominan las técnicas aritméticas. Esta categorización, que prima el control sobre el empleo del álgebra y no sobre el de la aritmética, se debe a que, desde los primeros cursos de la ESO, el objetivo es que los problemas verbales se resuelvan algebraicamente. Las técnicas aritméticas (o heurísticas) que, tras la educación primaria, todavía se enseñan, responden a la experiencia previa del alumnado (Khng y Lee, 2009) y deberían ser complementarias al aprendizaje del álgebra como motor de resolución.
La pertinencia de tomar en cuenta el grupo G2 se debe a un estudio previo (Gasco y Villarroel, 2012) que indica que un gran número de sujetos usa la aritmética en problemas adecuados para ello y sin embargo emplea el álgebra para resolver otros de muy difícil desarrollo aritmético.
El enunciado de los problemas se ha presentado en euskera o en castellano, dependiendo del modelo lingüístico del centro educativo.
ProcedimientoCon el fin de realizar la recogida de datos, se ha solicitado una cita con la dirección de cada centro elegido. Una vez obtenido el visto bueno, se expone la naturaleza de la investigación y las pruebas propuestas al profesorado de matemáticas de 2.°, 3.° y 4.° de la ESO. Cuando el profesorado acepta realizar la prueba en su aula, se acuerda una hora lectiva para llevarla a cabo. Las 2 únicas condiciones propuestas para la investigación son, por una parte, que la unidad didáctica referida a la resolución de problemas aritmético-algebraicos se haya impartido y finalizado con anterioridad a la fecha de la prueba y, por otra, que no se revele al alumnado la naturaleza concreta de la prueba matemática, más allá de comentar que se tendrán que hacer unos ejercicios matemáticos, sin especificar que serán problemas aritmético-algebraicos.
Se asegura la presencia en el momento de la administración de la prueba. Previamente al comienzo de la misma, se advierte que la prueba es anónima y que los datos personales que se requieren son la fecha de nacimiento y el sexo. Además, se informa de que los resultados obtenidos no influirán en la calificación escolar.
Dependiendo de cada individuo, la realización de la prueba ha tenido una duración de 10 a 25 min.
Finalmente, se adquiere el compromiso con el profesorado para dar información sobre los datos obtenidos una vez se hayan publicado.
Análisis de datosTras la corrección en papel de los problemas verbales aritmético-algebraicos, todos los datos obtenidos han sido guardados en una tabla de Excel.
El test empleado en el análisis estadístico ha sido la Chi cuadrado de Pearson. El análisis de dichos datos se ha realizado mediante el software estadístico PASW Statistics 18.
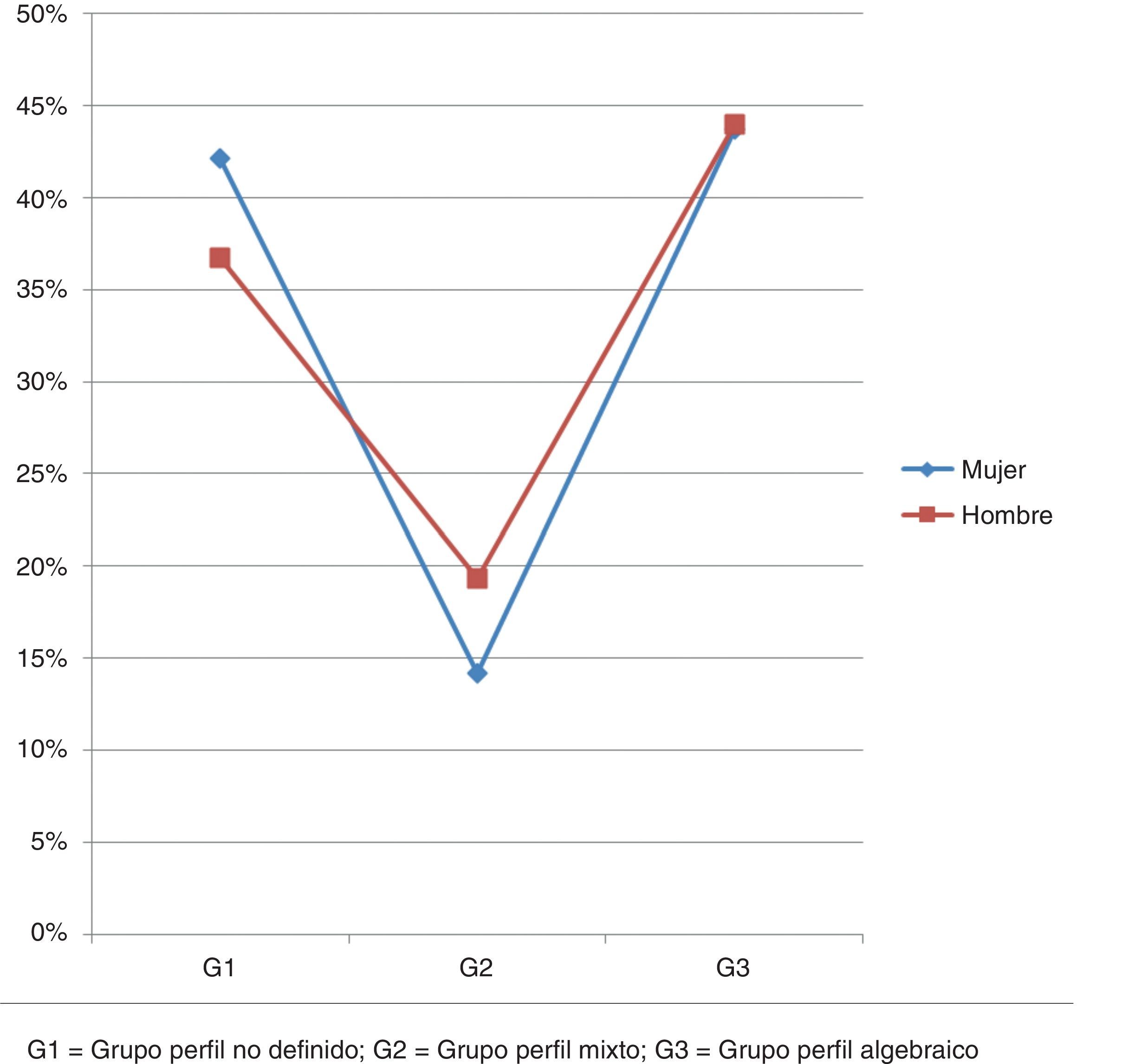
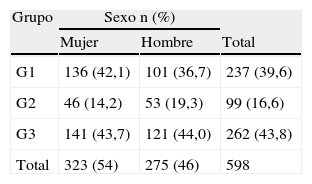
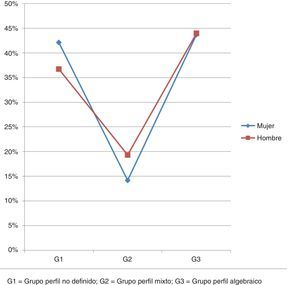
ResultadosEn la tabla 2 se exponen las distribuciones de los grupos de resolución de problemas en función del sexo:
Distribución de los grupos de resolución de problemas en función del sexo en los 3 cursos (frecuencias absolutas y porcentajes)
| Grupo | Sexo n (%) | ||
| Mujer | Hombre | Total | |
| G1 | 136 (42,1) | 101 (36,7) | 237 (39,6) |
| G2 | 46 (14,2) | 53 (19,3) | 99 (16,6) |
| G3 | 141 (43,7) | 121 (44,0) | 262 (43,8) |
| Total | 323 (54) | 275 (46) | 598 |
G1: grupo perfil no definido; G2: grupo perfil mixto; G3: grupo perfil algebraico.
No se ha encontrado relación entre la forma de resolver los problemas y el sexo del alumnado analizado como indica el test de Chi cuadrado de Pearson siguiente: X2(2; N=598)=3,3; p>0,05. En este caso se ha tenido en cuenta el total del alumnado de los 3 cursos. Las porcentajes expuestos confirman el resultado del test: la diferencia máxima entre sexos es de 5,4%. Según estos resultados, los chicos y las chicas emplean el álgebra y la aritmética con frecuencia similar en el momento de resolver problemas.
En la figura 1 se muestran los porcentajes descritos en la tabla 2:
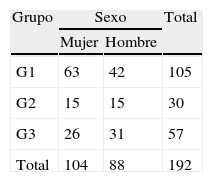
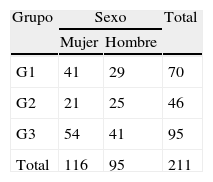
Atendiendo a los datos de cada curso, el test de Chi cuadrado muestra la misma tendencia en los 3 casos (2.°, 3.° y 4.° cursos). En la tabla 3 se presentan los datos obtenidos en 2.° curso de la ESO:
El test arroja los siguientes resultados: X2(2; N=192)=3,2; p>0,05.
En la tabla 4 se muestran los resultados concernientes a 3.°:
La Chi cuadrado ha resultado de la siguiente manera: X2(2; N=211)=2,1; p>0,05.
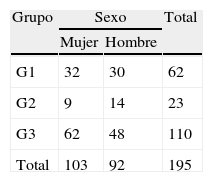
En la tabla 5 se presentan los datos recopilados en 4.° curso:
El test estadístico ofrece el siguiente resultado: X2(2; N=195)=2,3, p>0,5.
Discusión y conclusionesLos resultados indican que no se dan variaciones estadísticamente significativas entre los grupos de resolución en lo que respecta a alumnas y alumnos, o expresado de otra forma, ambos colectivos presentan perfiles de resolución parecidos.
La investigación sobre las diferencias de sexo en matemáticas ha tenido una gran repercusión en las últimas décadas, aunque recientemente no tiene la relevancia que tuvo en el pasado. Los estudios pioneros en este ámbito eran prácticamente unánimes al afirmar que en la competencia matemática los hombres obtenían mejores resultados que las mujeres tanto en la edad temprana como en la adulta (Maccoby, 1990).
En lo que a la resolución de problemas matemáticos respecta, los diversos estudios realizados revelan que la cuestión de las diferencias de sexo es muy compleja (Zhu, 2007). Se reporta una tendencia al alza en la ventaja masculina a medida que aumenta la edad del alumnado y se hace más patente a partir de los 14 años (educación secundaria) hasta la universidad (Hyde, Fennema y Lamon, 1990). Sin embargo, se han hallado diferentes patrones de resolución entre alumnos y alumnas consistentes en el uso de diferentes estrategias y observados desde la etapa de enseñanza elemental (Carr y Davis, 2001).
Estas estrategias se relacionan con las capacidades cognitivas y las características psicológicas y están mediadas por la experiencia y la educación. Los patrones de resolución diferentes entre chicos y chicas se deben a factores que intervienen en dicha resolución tales como las habilidades cognitivas (Nuttall et al., 2005), la velocidad de procesamiento de la información (Geary, Saults, Liu y Hoard, 2000), las diferencias fisiológicas en el cerebro (Rilea et al., 2004), la influencia de las hormonas sexuales (Halpern et al., 2005), los estilos de aprendizaje (Schwartz y Hanson, 1992), las actitudes hacia las matemáticas (Caplan y Caplan, 2005), los estereotipos de género del enunciado del problema (Spencer, Steele y Quinn, 1999) y el impacto de las variables socioeconómicas (Levine, Vasilyeva, Lourenco, Newcombe y Huttenlocher, 2005). La contribución de estos factores en las diferencias de sexo a la hora de resolver problemas matemáticos está todavía en fase de estudio y solo son aplicables en edades y contextos concretos y, por tanto, no deben ser generalizables (Zhu, 2007). Todas estas claves ofrecen una visión de la complejidad de la problemática en cuestión.
Como dato parcial, resulta significativo el informe PISA 2003 (IE, 2008) que realiza un estudio sobre las competencias matemáticas, entre otras, evaluando a alumnado de 4.° de la ESO de 25 países. Una de las 4 áreas evaluadas en matemáticas es la escala de cambio y relaciones, asociada a la resolución de problemas; a pesar de haber diferencias a favor de los alumnos en todas las áreas de matemáticas, en dicha escala las diferencias son más débiles en el Estado español. En informes internacionales posteriores, los resultados obtenidos no son específicos ya que se refieren al rendimiento matemático en general. En ambos diagnósticos se observa un rendimiento superior por parte del alumnado masculino; en el caso del Estado español la diferencia es estadísticamente significativa tanto en 2012 (IE, 2013) como en 2009 (IE, 2010; OECD, 2010) y 2006 (IE, 2007). En el País Vasco los resultados han sido dispares: no se han encontrado diferencias estadísticamente significativas ni en 2006 ni en 2009, aunque sí en 2012 y en el mismo sentido (IE, 2007; IE, 2010; IE, 2013).
Puede considerarse una contribución notable la ausencia de diferencias resultante de este estudio. Cabe destacar que, en educación secundaria, no hay apenas estudios que indaguen en la diferencia entre la resolución de problemas aritmético-algebraicos y el sexo. Como se ha mencionado anteriormente, algunas investigaciones encuentran diferencias significativas en el periodo de educación secundaria, que comprende los cursos 3.° y 4.° de la ESO y los 2 siguientes de Bachillerato. En consecuencia, no se ajusta a los cursos estudiados en esta investigación. Además, si, como se apunta en otros estudios, la diferencia crece con el avance de nivel académico, la ausencia de diferencias era probable, teniendo en consideración los cursos analizados, todavía en periodo inicial.
Habría que mencionar ciertas limitaciones del estudio. Sería conveniente estudiar una muestra que abarcara un mayor número de ciclos educativos con el fin de hacer un diagnóstico más real sobre las diferencias de sexo en la resolución de problemas. Además, la elección de la muestra no garantiza la generalización de los resultados, por lo que se recomienda seguir investigando en este sentido. Asimismo, un mayor número de problemas quizás ofrecería una categorización más exhaustiva de los grupos de resolución.
Finalmente, de cara a futuras investigaciones, se estima muy interesante explorar los métodos de resolución de problemas en otras disciplinas científicas más allá de las matemáticas, así como implementar estudios longitudinales con el fin de observar los cambios en las estrategias de resolución en función de la instrucción planificada.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
- 1.
Se reparten caramelos entre Jon y Maitane. A Jon le dan 5 caramelos más que a Maitane. En total hay 47 caramelos. ¿Cuántos caramelos le tocan a cada uno?
- 2.
Un grupo de estudiantes hace un viaje de 3 días. La distancia recorrida el segundo día es de 85km más que el primer día. La distancia recorrida el tercer día es de 125km más que el primero. La distancia total es de 1.410km. ¿Qué distancia se recorre cada día?
- 3.
Descubre el número que si lo multiplico por 8, resto 3 y divido por 3, el resultado es el doble del número que había pensado.