El trabajo que presentamos forma parte del Proyecto I+D SEJ-2007-66967 centrado en la evaluación educativa de la competencia de Aprender cómo Aprender. El propósito principal del estudio ha sido analizar el potencial de las evaluaciones externas y diagnósticas para estimar el grado de adquisición de estas competencias.
Se han analizado las pruebas de la Evaluación Diagnóstica de la Junta de Andalucía en el área de la ‘Competencia Matemática’ (2006-2007/2009-2010). La metodología empleada se basa en análisis cualitativos y cuantitativos de las diversas pruebas en función de una matriz de categorización de capacidades implicadas, distinguiendo entre el porcentaje de capacidades presentes y el nivel de dificultad en el que aparecen.
La evolución de las pruebas en Primaria y en Secundaria ha sido similar, tanto en los tipos de pruebas como en los niveles de dificultad. De las capacidades predominantes, ‘aplicación’ y ‘comprensión’ son las que están más presentes, aunque en un nivel básico. Por el contrario, los ítems que incluyen la ‘argumentación/comunicación’ han evolucionado en sentido descendente.
A la luz de los resultados obtenidos, valoramos la distancia existente entre el concepto de competencia propuesto en DeSeCo (OECD, 2005) y lo que realmente parecen evaluar estas pruebas.
The present paper is part of the R & D Project SEJ 2007-66967 focused educational competency assessment Learning how to Learn. The main purpose of the study was to analyze the potential of external and diagnostic to estimate the degree of acquisition of these skills assessments.
We analyzed tests Diagnostic Evaluation of Andalusia in the area of ‘Mathematics Competition’ (2006-2007 / 2009-2010). The methodology is based on qualitative and quantitative analysis of the various tests based on a matrix categorization capabilities involved, distinguishing between the percentage of current capabilities and the level of difficulty in which they appear.
The evolving evidence in Primary and Secondary was similar in both types of tests and levels of difficulty. About the predominant capabilities, ‘application’ and ‘understanding’ are those that are more present, even at a basic level. By contrast, items including ‘argument/communication’ downstream evolved.
In light of the results obtained, we value the distance between the concept proposed in DeSeCo (OECD, 2005) and it really seems to evaluate these tests.
El presente artículo recopila los hallazgos más sobresalientes de la investigación sobre las pruebas en el área competencia matemática de la Evaluación Diagnóstica en Andalucía. Para ello, se ha realizado el análisis de los cuadernillos de matemáticas tanto de Educación Primaria como de Secundaria de los cursos académicos 2006/2007, 2007/2008, 2008/2009 y 2009/2010.
Mención especial merece el hecho de que, en el curso 2006/2007, año en el que vio la luz la normativa española en materia de competencias básicas, no existían precedentes normativos con relación a la integración de dichas competencias en el currículum de las comunidades autónomas, salvo algunas experiencias innovadoras poco difundidas. Por ello, hay que destacar que la Evaluación Diagnóstica de Andalucía ha sido pionera en su aplicación a nivel censal. A ello hay que añadir que, en España, no había referentes consolidados sobre evaluación de competencias, a excepción de las pruebas PISA (que empezaron a aplicarse en el año 2000). Dichas pruebas poseen notables diferencias con respecto a las Pruebas de Evaluación Diagnóstica.
Teniendo en cuenta estos breves antecedentes, a lo largo de las siguientes páginas se ofrece un recorrido por el marco general de la investigación en la que se contextualiza el análisis de las pruebas del programa de Evaluación Diagnóstica de la Junta de Andalucía, así como una contextualización teórica de dichas pruebas en el área de matemáticas. Seguidamente, se abordará la descripción del proceso metodológico llevado a cabo en el análisis de las diferentes pruebas; y, por último, se ofrecen los resultados más relevantes de la investigación, así como la discusión de los hallazgos.
Marco general de la investigaciónEl propósito general del proyecto I+D SEJ 2007-66967 en el que se inserta esta investigación es conocer en qué medida los cuadernillos de Evaluación Diagnóstica de Andalucía miden competencias de primer y segundo orden, es decir, si realmente evalúan lo que dicen medir.
Para dar respuesta a este objetivo, se ha tratado de comprender y delimitar la complejidad de competencias, así como de los procesos incluidos en los aprendizajes de segundo orden denominados aprender cómo aprender (Hargreaves, 2005), estableciendo un marco operativo que identifique los componentes básicos de dichas competencias.
Los aprendizajes de orden superior son constructos complejos que incluyen inseparables factores cognitivos y afectivos, que suponen un propósito de autorregulación del proceso de aprender, una decidida tendencia a comprender los procesos en sus contextos, con el objetivo de facilitar la actuación competente del sujeto en su entorno, en función del propio proyecto personal, social o profesional (Gimeno Sacristán, 2008). Por tanto, la evaluación de los aprendizajes de segundo orden requiere la atención simultánea tanto a los factores cognitivos de orden superior como a los factores afectivos o motivacionales que impulsan y estimulan los movimientos de los aprendices (Pérez Gómez, 2007, 2008).
En consonancia con esto, la evaluación externa de los rendimientos educativos, basada en tests estandarizados, como es el caso de la Evaluación de Diagnóstico de Andalucía, ha ido evolucionando desde la medición de aspectos puramente cognitivos a la intención de medir competencias complejas en contextos reales. Como consecuencia, la evaluación externa ha intentado proporcionar información útil que los docentes puedan utilizar a la hora de analizar sus prácticas, al mismo tiempo que ha intentado informar a la sociedad y a la administración educativa. Pero esta evolución es lenta y refleja las contradicciones de intentar medir competencias complejas en situaciones reales con pruebas estandarizadas de lápiz y papel (Monereo y Pozo, 2007; Cumming y Wyatt-Smith, 2009; Serván Núñez, 2011; Pérez Gómez y Soto Gómez, 2011). La evaluación de competencias, por tanto, no se realiza sobre contenidos aprendidos, sino sobre la capacidad de utilizar los aprendizajes en distintas situaciones (Sierra, Méndez-Giménez y Mañana, 2013), lo cual es muy difícil de evaluar mediante dichas pruebas estandarizadas.
La competencia matemática en el Marco General de la Evaluación de Diagnóstico en AndalucíaLa Orden de 28 de junio de 2006 regula las pruebas de la Evaluación de Diagnóstico y el procedimiento de aplicación en los centros docentes andaluces. Estas pruebas se centran en la evaluación del rendimiento del alumnado en las competencias denominadas «básicas», con la finalidad de proporcionar información a los centros, al profesorado y a las familias para plantear acciones de mejoras educativas (Rodríguez Martínez, 2011).
Las pruebas de la Evaluación de Diagnóstico en Andalucía son realizadas por el alumnado de 4.° curso de Educación Primaria y del 2.° curso de Educación Secundaria Obligatoria.
El concepto de competencia en el que se sitúa este modelo de evaluación, según se indica en su marco teórico, se basa en los principios ya planteados por el proyecto DeSeCo (AA.VV., 2008), como ya hiciera también el programa PISA (Gallardo et al., 2010; Yus, Fernández y Gallardo, 2013).
En dicho proyecto, un grupo de expertos de la OCDE se encargó de definir y seleccionar las competencias consideradas esenciales para la vida de las personas y el buen funcionamiento de la sociedad en el siglo xxi. Desde estas premisas, se define el concepto de competencia como la capacidad de responder a demandas complejas y llevar a cabo tareas diversas de forma adecuada. Supone una combinación de habilidades prácticas, conocimientos, motivación, valores éticos, actitudes, emociones y otros componentes sociales y del comportamiento que se movilizan conjuntamente para lograr una acción eficaz (DeSeCo, 2005). Es decir, en el concepto de competencia subyacen procesos complejos que trascienden lo cognitivo (García Quiroga, Coronado y Montealegre, 2011). Una competencia supone un «saber», pero que se aplica; es decir, constituye un «saber hacer», susceptible de adecuarse a diversidad de contextos; posee un carácter integrador (cada competencia abarca conocimientos, procedimientos y actitudes); y se construye con la interrelación de saberes de los distintos ámbitos educativos.
En definitiva, se entiende por competencias básicas aquellas que permiten a los individuos lograr su realización personal y social y su inclusión laboral en la sociedad de la información y el conocimiento.
Al prestar atención al marco teórico establecido para las pruebas de diagnóstico del sistema educativo en la comunidad autónoma andaluza, se define la competencia matemática como: «La habilidad para utilizar sumas, restas, multiplicaciones, divisiones y fracciones en el cálculo mental o escrito con el fin de resolver diversos problemas en situaciones cotidianas. El énfasis se sitúa en el proceso y la actividad, aunque también en los conocimientos. La competencia matemática entraña (en distintos grados) la capacidad y la voluntad de utilizar modos matemáticos de pensamiento (pensamiento lógico y espacial) y representación (fórmulas, modelos, construcciones, gráficos y diagramas)» (AA.VV., 2006: 15).
En dicho documento, se insiste en que las pruebas deben basarse en situaciones-problemas. Pruebas que surjan de casos o situaciones que sustenten la interrogación y que, en la medida de lo posible, remitan a situaciones similares a las que el alumnado puede encontrar en su vida escolar o extraescolar. La competencia matemática, por tanto, es considerada parte principal de la preparación educativa, puesto que las ideas y los conceptos matemáticos son herramientas para actuar sobre la realidad (Rico, 2007); es más, el conocimiento matemático es una construcción personal y social de significados, el resultado de una evolución histórica, un proceso cultural en permanente desarrollo (D’Amore, Godino y Fandiño, 2008). Para la evaluación de la competencia matemática, se consideran aspectos que aluden a la capacidad de organizar, comprender e interpretar información, a la capacidad de expresión y a la capacidad para plantear y resolver problemas. El interés se centra en las capacidades de los sujetos para analizar y comprender las situaciones, identificar conceptos y procedimientos matemáticos aplicables, razonar sobre ellos, generar soluciones y expresar los resultados de manera adecuada.
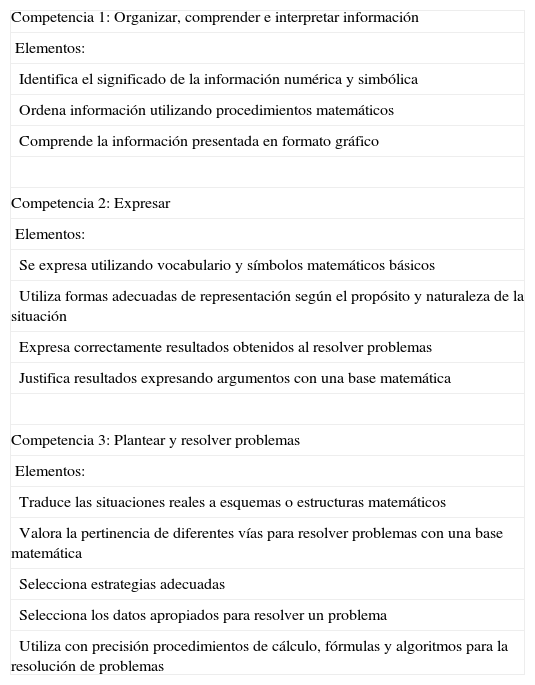
En el marco teórico de la Evaluación Diagnóstica de Andalucía se recogen las competencias y elementos de competencia que aparecen en la tabla 1 (Competencia matemática).
Competencia matemática
| Competencia 1: Organizar, comprender e interpretar información |
| Elementos: |
| Identifica el significado de la información numérica y simbólica |
| Ordena información utilizando procedimientos matemáticos |
| Comprende la información presentada en formato gráfico |
| Competencia 2: Expresar |
| Elementos: |
| Se expresa utilizando vocabulario y símbolos matemáticos básicos |
| Utiliza formas adecuadas de representación según el propósito y naturaleza de la situación |
| Expresa correctamente resultados obtenidos al resolver problemas |
| Justifica resultados expresando argumentos con una base matemática |
| Competencia 3: Plantear y resolver problemas |
| Elementos: |
| Traduce las situaciones reales a esquemas o estructuras matemáticos |
| Valora la pertinencia de diferentes vías para resolver problemas con una base matemática |
| Selecciona estrategias adecuadas |
| Selecciona los datos apropiados para resolver un problema |
| Utiliza con precisión procedimientos de cálculo, fórmulas y algoritmos para la resolución de problemas |
Fuente: AA.VV., 2006: 34.
Posteriormente, la competencia matemática o alfabetización matemática hace referencia a la capacidad del individuo para resolver situaciones prácticas cotidianas, utilizando para este fin los conceptos y procedimientos matemáticos (AA.VV., 2008). Esta competencia engloba las siguientes «dimensiones»: la capacidad de organizar, comprender e interpretar información; la capacidad de expresión; y la capacidad para plantear y resolver problemas.
El desglose de esta competencia, a su vez, en elementos de competencia (Íbidem, 2008) da lugar a que se focalice el interés sobre las capacidades de los sujetos para: analizar y comprender las situaciones; identificar conceptos y procedimientos matemáticos aplicables; razonar sobre ellos; generar soluciones; y expresar los resultados de manera adecuada.
Según los presupuestos teóricos de la evaluación diagnóstica, el dominio de estas capacidades revelará en qué grado el alumnado es competente para hacer uso de las matemáticas en escenarios reales y diversos de su vida cotidiana, aunque existen pocos estudios centrados en el análisis del diseño de los cuadernillos de evaluación de las pruebas (Fernández-Alonso y Muñiz, 2011).
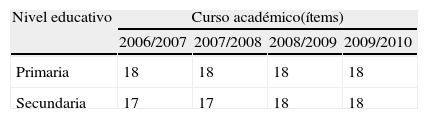
MétodoLa investigación se ha basado tanto en un análisis cuantitativo como cualitativo de las pruebas de Evaluación Diagnóstica. En la tabla 2, podemos ver los ítems analizados en cada prueba por año.
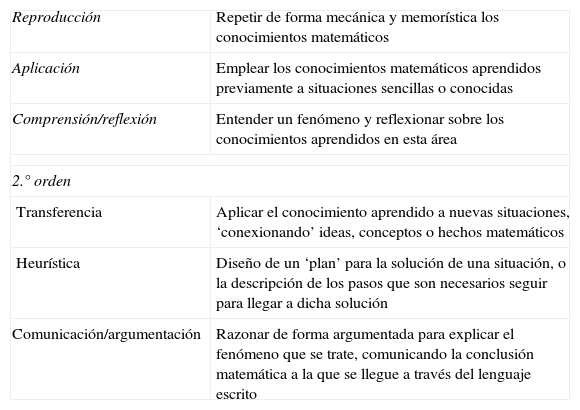
La metodología utilizada se ha centrado en el análisis de contenido de las pruebas por grupos de expertos, que han valorado independientemente los ítems de cada prueba en función de los apartados establecidos en una ficha de análisis, que posteriormente fue volcada en el paquete estadístico SPSS v. 22 para su tratamiento informático. Cada prueba fue sometida a un acuerdo interjueces y al juicio de un nuevo experto en las adscripciones de aquellos ítems que manifestaban importantes discrepancias en la valoración inicial. Para realizar el análisis de contenido, se tuvo como referencia la matriz de capacidades cognitivas que mostramos en la tabla 3.
Capacidades cognitivas
| Reproducción | Repetir de forma mecánica y memorística los conocimientos matemáticos |
| Aplicación | Emplear los conocimientos matemáticos aprendidos previamente a situaciones sencillas o conocidas |
| Comprensión/reflexión | Entender un fenómeno y reflexionar sobre los conocimientos aprendidos en esta área |
| 2.° orden | |
| Transferencia | Aplicar el conocimiento aprendido a nuevas situaciones, ‘conexionando’ ideas, conceptos o hechos matemáticos |
| Heurística | Diseño de un ‘plan’ para la solución de una situación, o la descripción de los pasos que son necesarios seguir para llegar a dicha solución |
| Comunicación/argumentación | Razonar de forma argumentada para explicar el fenómeno que se trate, comunicando la conclusión matemática a la que se llegue a través del lenguaje escrito |
Fuente: Elaboración propia.
Estas categorías de capacidades cognitivas fueron analizadas en función de su predominancia en las diferentes pruebas, para lo que se establecieron 3 niveles: 0-no presente; 1-escasamente presente; 2-moderadamente presente; 3-muy presente.
La matriz de capacidades definida es similar a la establecida en los trabajos de Hopmann, Brinek y Retzl (2007) de la Universidad de Viena, donde analizan y comparan las categorías cognitivas implícitas en las pruebas de PISA, con relación a las pruebas diagnósticas realizadas en Francia, Alemania y Finlandia. Estos autores siguen las revisiones críticas de la taxonomía de Bloom elaboradas por Anderson y Krathwohl (2001).
Como bien se indica en la tabla 3, las capacidades reconocer, recordar, comprender el sentido de términos y proposiciones sencillas, así como aplicar fórmulas o procedimientos sencillos de forma mecánica, han sido consideradas como cualidades cognitivas de orden inferior o de primer orden; mientras que el análisis, la transferencia compleja, la evaluación y la creación se han identificado como cualidades cognitivas de orden superior o de segundo orden.
Para complementar el análisis descriptivo del estudio, se realizó una ANOVA de un factor para delimitar si existían diferencias significativas de variabilidad de las medias de las distintas capacidades observadas en los ítems de los cuadernillos tanto de Primaria como de Secundaria.
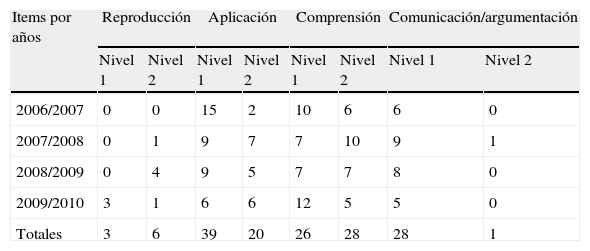
ResultadosCon respecto a las capacidades en las pruebas de Educación Primaria, no se ha encontrado ningún ítem en el que estén presentes las capacidades definidas como transferencia o heurística. La capacidad de reproducción tiene escasa presencia, pero es destacable el hecho de que, cuando aparece, lo hace en un nivel 2, al solicitar al alumnado la memorización de conceptos como la clasificación de ángulos o definir perímetros (conceptos introducidos en el segundo ciclo de Educación Primaria). En el curso 2006/2007, no se les pedía a los estudiantes la memorización de hechos o conceptos, sin embargo, en los cursos siguientes, los estudiantes tienen que responder a preguntas tales como qué es el perímetro o cómo se denominan determinados ángulos o figuras, aumentando, por tanto, la capacidad de reproducción a lo largo de los años. Las capacidades de aplicación y comprensión son las que tienen mayor presencia en todas las pruebas; al observar la evolución a través de los cursos, se aprecia cómo en el curso 2006/2007 hay más pruebas en el nivel 1 en ambas capacidades, lo que sugiere una menor dificultad para los estudiantes. En el curso 2007/2008, hay un mayor número de pruebas en el nivel 2 y, por tanto, las pruebas resultan más complicadas; en el 2008/2009, parece que existe la tendencia a un cierto equilibrio entre el número de pruebas en cada nivel, aunque hay que señalar que en este curso una buena parte de las preguntas constan de varios apartados y esto hace que la demanda de atención y tiempo necesario sea mayor. En el primer año, prácticamente todas las preguntas se refieren a una única cuestión, mientras que en los últimos años se aumentan las demandas al alumnado, ya que en alguna de las preguntas se le pide que responda hasta 4 cuestiones. En Primaria, la capacidad de comunicación/argumentación está prácticamente situada en el nivel 1, pues no requiere un nivel de argumentación elaborado; en su mayoría, se trata de escribir la cadena de operaciones para resolver un problema o justificar una respuesta por el resultado de una operación, sin razonamiento por escrito. Todo ello se observa en la tabla 4 (Capacidades por niveles según curso académico en Primaria).
Capacidades por niveles según curso académico en Primaria
| Items por años | Reproducción | Aplicación | Comprensión | Comunicación/argumentación | ||||
| Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | |
| 2006/2007 | 0 | 0 | 15 | 2 | 10 | 6 | 6 | 0 |
| 2007/2008 | 0 | 1 | 9 | 7 | 7 | 10 | 9 | 1 |
| 2008/2009 | 0 | 4 | 9 | 5 | 7 | 7 | 8 | 0 |
| 2009/2010 | 3 | 1 | 6 | 6 | 12 | 5 | 5 | 0 |
| Totales | 3 | 6 | 39 | 20 | 26 | 28 | 28 | 1 |
Fuente: Elaboración propia.
Si se compara la tendencia a la utilización de cada una de las capacidades por año, se aprecia que no existe una tendencia uniforme, por regla general, excepto en la capacidad de aplicación, que ha sido a la baja.
En la tabla 5 (Valoración de las capacidades por curso académico en Primaria), podemos ver los resultados obtenidos del contraste de medias entre las distintas capacidades.
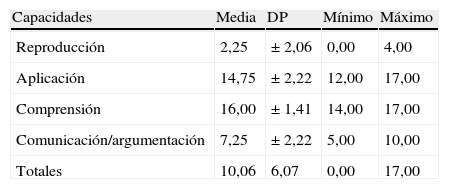
Valoración de las capacidades por curso académico en Primaria
| Capacidades | Media | DP | Mínimo | Máximo |
| Reproducción | 2,25 | ± 2,06 | 0,00 | 4,00 |
| Aplicación | 14,75 | ± 2,22 | 12,00 | 17,00 |
| Comprensión | 16,00 | ± 1,41 | 14,00 | 17,00 |
| Comunicación/argumentación | 7,25 | ± 2,22 | 5,00 | 10,00 |
| Totales | 10,06 | 6,07 | 0,00 | 17,00 |
Fuente: Elaboración propia.
En este análisis, las competencias son significativamente diferentes según el número de ítems (F=41,83 con un nivel de significación p=0,001); esas diferencias son elevadas por juzgar el tamaño del efecto (eta-cuadrado), siendo su valor de 0,913. Las pruebas post hoc informaron que las principales diferencias se encontraban entre la competencia de reproducción y las demás. En definitiva, los grupos de capacidades que difieren con mayor significatividad son las capacidades de reproducción y comunicación/argumentación, de las capacidades de aplicación y comprensión. No obstante, es de resaltar que las capacidades de reproducción y comunicación/argumentación, aunque difieren, no presentan una diferencia muy significativa.
Centrando el análisis en los cuadernillos de Secundaria, sí se puede observar una gran variación en la comunicación/argumentación. En el primer año, casi la mitad de las pruebas exige una justificación, explicación o reflejar cálculos, mientras que en el último año no se solicita en ninguna de las pruebas; es más, se ha ido reduciendo esa exigencia a lo largo de los años, hasta desaparecer. En cuanto a la solicitud de explicar procesos o soluciones, se ha producido una gran variabilidad a lo largo de los años, sobre todo, en Secundaria. En el curso 2006/2007, se pide al alumnado la explicación del proceso seguido para la resolución en 9 ítems de los 17 ítems analizados; este requerimiento de explicación, se limita a 5 preguntas en el 2007/2008, una en el 2008/2009 y ninguna en el curso 2009/2010.
Por otro lado, la capacidad de transferencia está muy poco presente en las pruebas, así como la heurística, que está presente solo en 2 de los cursos y en pruebas conocidas como «pasatiempos».
La capacidad de aplicación sí está presente en todos los cursos y en una buena parte de las pruebas. Dentro de esta capacidad se han incluido aquellos ítems que requieren la utilización de operaciones, porcentajes o lectura de gráficas.
Al tener en cuenta los niveles, podemos observar cómo el nivel 1 es el que prevalece en las capacidades de aplicación y comunicación/argumentación. Esto puede ser debido a que los conceptos, algoritmos o fórmulas que se aplican son, en la mayoría de los casos, pruebas sencillas (se trata de aplicar, generalmente, operaciones básicas o interpretar gráficas simples). En la capacidad de comprensión, sin embargo, sucede lo contrario, predomina el nivel 2, salvo en el curso 2006/2007. El nivel 1 se caracteriza por problemas que se resuelven con una operación básica o interpretación de gráficas sencillas, y la mayoría de las pruebas requieren algo más que esto. En la tabla 6 (Capacidades por niveles según curso académico en Secundaria), se observa la distribución de las capacidades por años y por niveles.
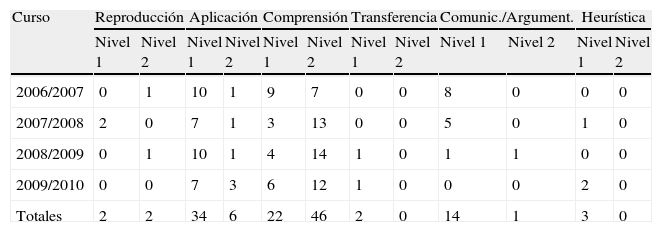
Capacidades por niveles según curso académico en Secundaria
| Curso | Reproducción | Aplicación | Comprensión | Transferencia | Comunic./Argument. | Heurística | ||||||
| Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | Nivel 1 | Nivel 2 | |
| 2006/2007 | 0 | 1 | 10 | 1 | 9 | 7 | 0 | 0 | 8 | 0 | 0 | 0 |
| 2007/2008 | 2 | 0 | 7 | 1 | 3 | 13 | 0 | 0 | 5 | 0 | 1 | 0 |
| 2008/2009 | 0 | 1 | 10 | 1 | 4 | 14 | 1 | 0 | 1 | 1 | 0 | 0 |
| 2009/2010 | 0 | 0 | 7 | 3 | 6 | 12 | 1 | 0 | 0 | 0 | 2 | 0 |
| Totales | 2 | 2 | 34 | 6 | 22 | 46 | 2 | 0 | 14 | 1 | 3 | 0 |
Fuente: Elaboración propia.
Como se puede apreciar en la tabla anterior, la capacidad de comprensión es la que tiene una mayor presencia, lo que es natural, pues es una de las más amplias según las capacidades definidas por la comisión. De hecho, cualquier prueba que no sea mera reproducción o una simple aplicación de algoritmos o fórmulas requiere de la comprensión para su realización. En las únicas pruebas donde no está presente esta capacidad es en 3 de las pruebas de reproducción.
Al igual que en Primaria, en Secundaria, se ha comparado la tendencia de evolución de las capacidades en los distintos cursos académicos, como se puede ver en la tabla 7 (Valoración de las capacidades por curso en Secundaria).
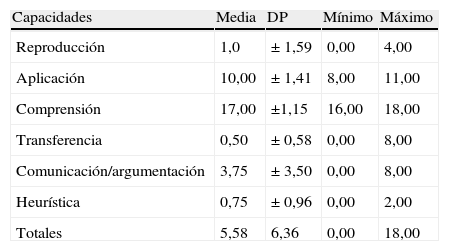
Valoración de las capacidades por curso en Secundaria
| Capacidades | Media | DP | Mínimo | Máximo |
| Reproducción | 1,0 | ± 1,59 | 0,00 | 4,00 |
| Aplicación | 10,00 | ± 1,41 | 8,00 | 11,00 |
| Comprensión | 17,00 | ±1,15 | 16,00 | 18,00 |
| Transferencia | 0,50 | ± 0,58 | 0,00 | 8,00 |
| Comunicación/argumentación | 3,75 | ± 3,50 | 0,00 | 8,00 |
| Heurística | 0,75 | ± 0,96 | 0,00 | 2,00 |
| Totales | 5,58 | 6,36 | 0,00 | 18,00 |
Fuente: Elaboración propia.
Al realizar la ANOVA de un factor, se aprecian diferencias significativas (F=49,99 con un nivel de significación p=0,001); estas diferencias son relativamente elevadas según el tamaño del efecto, con un valor de 0,781. En las pruebas post hoc, se aprecia que, entre las capacidades de reproducción, transferencia y heurística, hay más diferencia que entre la capacidad de comunicación/argumentación. La mayor diferencia estadísticamente significativa está presente en la capacidad de comprensión. Aunque entre aplicación y comprensión también existen diferencias, no son tan distantes como ocurre con las demás capacidades.
Por otro lado, realizando un análisis más cualitativo centrado en los contenidos y dimensiones que se determinan en los cuadernillos de la Junta de Andalucía, parece que las actividades deben referirse a contextos reales y cercanos a los estudiantes, pero en algunas ocasiones se presentan situaciones que, aunque puedan estar inmersas en un contexto real, este contexto es un mero recurso para preguntar alguna cuestión referente a la materia. Prácticamente todas las actividades son similares a las tareas escolares que están presentes en los libros de texto en cuanto a lo que a formato y lenguaje respecta. En los cuadernillos, están presentes situaciones puramente matemáticas, como escribir la fórmula para calcular el área de un rectángulo. Algunos ítems quieren situar los conocimientos en un entorno cotidiano o real, pero son totalmente artificiales, como el ítem 9 del curso 2006/2007, en el que se presenta a un vendedor de globos con formas de poliedros, tales como el tetraedro y el icosaedro, y se preguntan los nombres de las formas geométricas.
Por otra parte, es destacable el hecho de que cada una de las pruebas solo está asignada a un bloque de contenidos y en algunas de las pruebas la asignación no parece acertada, como sucede en la prueba 3 del curso 2006/2007. En dicha prueba, aparecen figuras geométricas, pero no es necesario identificarlas ni utilizar ningún conocimiento geométrico, ya que se pide al alumnado que rellene una tabla con los datos numéricos que se proporcionan. En este caso, la prueba se podría identificar dentro del bloque representación de la información e incluso aritmética y medida. Una buena parte de las pruebas son problemas aritméticos verbales, que claramente pertenecen al bloque de aritmética, pero algunas de ellas, en la descripción, se incluyen dentro del bloque de representación de la información, porque se pide que se vayan colocando los resultados en una tabla (ej.: pregunta 5 del curso 2007/2008). En Secundaria, también hay pruebas en las que las cuestiones que se plantean pertenecen a más de un bloque. Por ejemplo, la pregunta del año 2007/2008 en la que se pide el área de un rectángulo en función de los lados. Dicho ítem está asignado al bloque de álgebra, pero también es un concepto geométrico. Otro ejemplo puede ser la pregunta 7 del curso 2006/2007, la cual está asignada al bloque de geometría porque se presenta un patrón geométrico, aunque lo que se pide es la búsqueda de una serie numérica y, por tanto, pertenece al bloque de números.
No parece estar clara la asignación a cada dimensión y cada elemento de competencia. Como ya se ha indicado, cada pregunta está asignada a una sola dimensión y a un elemento de competencia, lo cual hace que las asignaciones puedan ser diferentes, aunque sean pruebas similares. Un elemento de la dimensión expresión matemática es: «Expresa correctamente los resultados obtenidos al resolver un problema»; en este caso, nos encontramos con preguntas que plantean la resolución de un problema y no están dentro de la dimensión plantear y resolver problemas, sino en expresión matemática y el elemento de competencia que se refiere a expresar correctamente los resultados, cuando debería estar asignada a las 2 dimensiones. Con la dimensión organizar, comprender e interpretar información, así como con la dimensión plantear y resolver problemas pasa algo parecido. La resolución de un problema suele implicar comprender, organizar o interpretar información numérica o simbólica, además requiere que se expresen correctamente resultados e incluso procedimientos de resolución.
Asignar solo una dimensión y un elemento de competencia es algo irreal, por ejemplo, al hacer referencia al elemento de competencia selecciona los datos apropiados para la resolución del problema, este elemento está presente, sobre todo, cuando se muestra información irrelevante. Aunque tras la selección de los datos correctos haya que resolver el problema, y para ello el estudiante tenga que traducir una situación verbal a una cadena de operaciones, que es otro elemento de competencia, de la dimensión plantear y resolver problemas, en el caso de tratarse de un problema aritmético verbal, o bien, seleccionar la estrategia adecuada para resolver el problema (tercer elemento de competencia de la dimensión plantear y resolver problemas) y tras el proceso de resolución, deberá expresar correctamente los resultados o incluso el proceso de resolución (dimensión de expresión matemática). Se podría pensar que se han asignado los diferentes ítems a las dimensiones según el peso que tiene en ellos cada dimensión, pero los ejemplos muestran discrepancias. Por ello, se puede decir que la asignación a una determinada dimensión o competencia es confusa, al no estar claro qué se está midiendo.
Con respecto al formato de pregunta, cabe indicar que, aunque el marco teórico plantea los diferentes formatos de preguntas (elección múltiple, abiertas o cerradas), en Secundaria solo se plantean 2 preguntas de elección múltiple (una en el curso 2007/2008 y otra en el curso 2009/2010), y 2 preguntas abiertas (una en el curso 2006/2007 y otra en el 2007/2008). El resto de las peguntas (67) son preguntas cerradas, solo admiten una solución. En el último año, aumentó considerablemente el número de cuestiones que tenían que responder los estudiantes y, por tanto, la complejidad de la prueba (pues el tiempo de aplicación sigue siendo el mismo). Otra diferencia en los 2 últimos años ha sido una mayor presencia de actividades puramente matemáticas, 6 de las 18 pruebas, mientras que en el curso 2006/2007 solo eran 3.
Con respecto al tratamiento de la geometría y el álgebra, cabe indicarse que se presenta una visión de la geometría, sobre todo en Primaria, centrada en recordar nombres e identificar polígonos o sólidos. Todas las pruebas clasificadas como de reproducción en Primaria son de geometría. La mayoría indican que se especifique qué tipo de polígono o sólido es una determinada figura, que el alumnado diga si es un ángulo recto, agudo u obtuso. De todas las pruebas de geometría que se proponen en Primaria (13 pruebas) entre el 2006 y el 2009, solo 2 de ellas están incluidas en la dimensión plantear y resolver problemas. En el curso 2009/2010, de las 6 pruebas de geometría, 4 son de reproducción (reconocer y nombrar polígonos, sólidos y ángulos), las otras 2 son cálculo de superficies, no hay nada de resolución de problemas.
En Primaria, salvo 2 pruebas en el curso 2007/2008 sobre rectángulos isoperimétricos e isométricos, las pruebas pertenecientes al bloque de geometría se reducen prácticamente a reconocer y nombrar polígonos, sólidos, ángulos, paralelas y perpendiculares, así como a la definición y cálculo de perímetros.
En Secundaria, el porcentaje de pruebas de geometría es menor que en Primaria (10 preguntas en los 4 cursos), 2 o 3 cada curso. Entre dichas pruebas también se encuentran otras de reconocimiento de polígonos y sólidos. En Secundaria, se introducen algunos aspectos nuevos, como son 2 pruebas de perspectivas y visualización espacial, una de cálculo de medidas en un mapa a partir de una escala, otra de cálculo de medidas de ángulos y un problema donde hay que aplicar el teorema de Pitágoras. En esta etapa, de las 10 pruebas de geometría, solo 3 de ellas están incluidas en la dimensión plantear y resolver problemas. En definitiva, se puede indicar que la visión de la geometría que muestran las pruebas de diagnóstico en la Educación Secundaria es limitada y no parece que esta área pueda contribuir a resolver problemas de la vida real, lo que no es adecuado en el marco de las competencias.
También sucede algo similar con el bloque de álgebra en Secundaria. La presencia de este bloque es escasa (9 pruebas), aunque ello puede estar justificado, pues estos contenidos se inician en la Educación Secundaria y los estudiantes no están tan familiarizados con ellos. De esas 9 pruebas, solo 2 se encuentran dentro de la dimensión plantear y resolver problemas, aunque la mayoría de las pruebas se refieran a reconocer o aplicar fórmulas, o a establecerlas a partir de un enunciado verbal, pero de una situación matemática. Prácticamente no existen problemas de la vida real en los que haya que traducir al lenguaje algebraico la situación planteada para su resolución, siendo este uno de los objetivos principales del álgebra en esa etapa. Solo uno de los problemas (balanza, pregunta 7, cuadernillo 2007/2008, Secundaria) presenta una situación relativamente cotidiana. En ese ítem, se trata de pesar en una balanza, lo cual, aunque puede conducir a una ecuación de primer grado para su resolución, no es una situación real.
Es destacable también el hecho de que un enfoque en competencias debe tender a la interdisciplinariedad, por lo que no se deberían plantear bloques tan separados dentro de una misma disciplina; de hecho, la orden que establece el currículum de la Educación Primaria en Andalucía hace hincapié en que hay que poner de manifiesto la conexión entre los diversos núcleos de contenidos.
Por último, si se establece una comparativa entre las pruebas de Primaria y Secundaria, resulta extraña la cuestión de que, en principio, algunas de las pruebas de Primaria sean más difíciles que algunas de Educación Secundaria y otras sean similares. Aunque a grandes rasgos la dificultad en ambos niveles educativos es similar, al igual que su evolución a lo largo de los cursos. En el primer año 2006/2007, las pruebas de nivel 1 eran mayoritarias, tanto en Primaria como en Secundaria, por lo que el nivel de dificultad de este año es menor que los restantes. En estos últimos 3 años, no obstante, no ha habido grandes variaciones en los niveles de dificultad, aunque sí se observa que en el último año hay preguntas que requieren 3 o más respuestas sobre una misma situación, lo que no es habitual en los cursos anteriores, en los que la mayoría de las preguntas solo requerían una respuesta.
DiscusiónDesde que empezaron a aplicarse estas pruebas en Andalucía, han ido evolucionando de manera similar en Primaria y en Secundaria. De todas las capacidades que se pretenden identificar, han sido las capacidades de aplicación y comprensión las que han tenido más presencia, aunque en un nivel de dificultad básico. Es destacable también el hecho de que, con los años, se ha ido aumentando el número de demandas al alumnado dentro de un ítem, llegando incluso a que una pregunta tenga 4 subapartados. Por otra parte, resulta también llamativo que el empleo de ítems que identifican la capacidad de argumentación/comunicación haya evolucionado en sentido descendente, reduciéndose a una mera exposición de los posibles cálculos a realizar en un determinado problema.
Tanto las pruebas de Primaria como las de Secundaria parecen reflejar una marcada influencia del formato de pregunta presente en los libros de textos, presentándose las pruebas con un estilo estándar: problemas cerrados en su mayoría y alejados de la realidad del estudiante en ocasiones. Así pues, aunque las pruebas pretenden reflejar un contexto real y cercano para los estudiantes, la formulación del ítem artificializa el ejercicio, utilizándose dicho contexto como un mero recurso para el empleo de algún procedimiento (operaciones, sobre todo). Asimismo, las preguntas hacen referencia a una única dimensión y bloque de contenido, cuando hay que tener en cuenta que algunos de estos ítems atañen a más de un bloque y a más de una dimensión. Esto refleja una imagen bastante parcelada y compartimentada del conocimiento matemático, a pesar de que los decretos referentes al currículum de matemáticas, tanto en Primaria como en Secundaria, proponen una visión más amplia que relacione los diferentes bloques e incluso que vaya más allá del propio conocimiento matemático, es decir, una visión del currículum más interdisciplinar, basada en el concepto de competencias educativas (otra cuestión claramente desaprovechada en esta evaluación).
En lo que respecta a la evolución a lo largo de estos años, no hay grandes variaciones en los tipos de pruebas y los niveles de dificultad son similares, salvo en la primera de ellas (curso 2006/2007), en la que las pruebas son algo más sencillas. Lo que sí se ha constatado es que, en el último año, han aumentado las demandas, pues en algunas de las pruebas se solicita resolver 3 o 4 preguntas dentro de un mismo ítem.
FinanciaciónProyecto I+D SEJ-2007-66967, dirigido por el profesor D. Ángel I. Pérez Gómez (Universidad de Málaga) y financiado por el Ministerio de Educación de España.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Agradecemos al Ministerio de Educación de España y al Servicio de Evaluación de la Junta de Andalucía su inestimable ayuda para el desarrollo de esta investigación.