El manejo de los pacientes con factores de riesgo cardiovascular precisa del cálculo del riesgo cardiovascular de los pacientes. Los objetivos terapéuticos de control de un factor de riesgo cardiovascular no dependen sólo de la intensidad de su alteración, sino también del riesgo cardiovascular total del paciente. Los diferentes criterios de abordaje del riesgo cardiovascular han ocasionado que existan en la actualidad varios sistemas de valoración del riesgo cardiovascular1-6.
La valoración del riesgo cardiovascular se puede realizar de forma cualitativa o cuantitativa. Un ejemplo de valoración cualitativa es la que ofrece la guía de hipertensión de la Sociedad Española de Hipertensión-Liga Española para la Lucha contra la Hipertensión Arterial (SEH-LEHLA)7, en la que el riesgo se calcula por el grado de hipertensión y la presencia o no de determinados factores de riesgo o lesiones de órganos diana o eventos cardiovasculares. Como ejemplos de sistemas cuantitativos de valoración del riesgo cardiovascular, tenemos las ecuaciones derivadas del estudio de Framingham8 y las derivadas del proyecto SCORE3. Una ventaja de los sistemas cuantitativos es que permiten ciertos cálculos basados en la reducción del riesgo con las intervenciones terapéuticas, como son la reducción absoluta y relativa del riesgo y el cálculo del número de pacientes que es necesario tratar para evitar un evento cardiovascular (NNT). En cambio, tienen otras desventajas, como que el número de factores que intervienen en el cálculo del riesgo es menor que en los sistemas cualitativos.
Cualquier sistema de estratificación o cálculo del riesgo cardiovascular debe adaptarse a la población a la que se quiera aplicar si ésta es diferente de la población de la que se obtuvo las ecuaciones, para evitar una valoración del riesgo exagerada o defectuosa. Así, las ecuaciones del estudio de Framingham deben adaptarse a nuestro medio. En España hay dos adaptaciones de dichas ecuaciones: las procedentes de los estudios REGICOR4 y DORICA5, cada una con una metodología similar, pero con diferente base poblacional. La adaptación se ha realizado mediante una calibración de la ecuación original.
La correcta valoración del riesgo cardiovascular tiene importancia tanto poblacional como individual. Importa conocer cuántos sujetos en una población están en alto riesgo cardiovascular, porque son sujetos que consumirán más recursos sanitarios tanto asistenciales como farmacológicos. Pero también es importante saber a escala individual si un sujeto resulta tener alto riesgo tanto con un sistema como con otro.
Los distintos sistemas de valoración tienen diferentes limitaciones. Además de la posible sobreestimación o subestimación del riesgo, éstas pueden ser diferentes según la edad y el sexo. También hay una limitación en la edad de aplicación de cada sistema de valoración. Con los sistemas de valoración del riesgo, los sujetos jóvenes no tienen riesgo alto, por lo que se ha propuesto el cálculo del riesgo relativo o la proyección a los 60 años como método para valorar el riesgo en los jóvenes6,9.
En el presente estudio se pretende valorar la concordancia de las ecuaciones original y calibradas al aplicarlas a una muestra de población general y presentar las ventajas que supone la aplicación de percentiles como alternativa o complementariamente a cualquiera de las ecuaciones calibradas.
Material y método
Se ha realizado un estudio transversal de prevalencia de factores de riesgo cardiovascular en la provincia de Palencia (España), como se ha publicado previamente10. Se ha seleccionado de la población general, mediante números aleatorios generados por ordenador, a 514 sujetos de ambos sexos en 9 centros de salud de la provincia de Palencia, de forma estratificada por edad y sexo, de 20 a 79 años de edad. A cada sujeto se le realizó una breve historia clínica dirigida, una exploración física y una exploración analítica, con objeto de valorar su riesgo coronario. Las variables analizadas han sido edad, sexo, antecedentes personales de eventos cardiovasculares previos, antecedentes familiares de enfermedad cardiovascular precoz, tabaquismo, presión arterial sistólica y diastólica, talla, peso, glucosa, glucohemoglobina si el paciente era diabético, colesterol total, colesterol de las lipoproteínas de alta densidad (cHDL) y colesterol de lipoproteínas de baja densidad (cLDL) y triglicéridos.
Para el cálculo de las prevalencias de diabetes, hipercolesterolemia e hipertensión arterial, se consideró a los pacientes diagnosticados y en tratamiento farmacológico o no farmacológico por sus médicos de atención primaria, así como a los sujetos que tuvieran glucemias basales en ayunas > 125 mg/dl11, colesterolemias basales en ayunas > 240 mg/dl12 y presión arterial sistólica o diastólica >= 140 mmHg o >= 90 mmHg, respectivamente13.
Para calcular el riesgo coronario se han aplicado las ecuaciones originales del estudio de Framingham en su versión de Wilson8, así como las calibraciones procedentes de los estudios REGICOR4 y DORICA5. Se considera riesgo alto cuando el riesgo coronario calculado a 10 años es >= 20%. A cada sujeto se le ha calculado el riesgo por los tres métodos. Se ha excluido a los sujetos con antecedentes de eventos cardiovasculares previos.
Una vez calculados los riesgos absolutos con cada ecuación, se han calculado los percentiles de riesgo coronario con cada ecuación. Cada sujeto ha sido situado en su percentil de riesgo. Se han comparado los riesgos absolutos con cada ecuación y también los percentiles asignados a cada sujeto con cada ecuación.
Se ha construido una gráfica de percentiles y se expone la posibilidad de proyección por el percentil de los sujetos jóvenes a los 60 años.
Análisis estadístico
Los datos de edad, exploración física y de laboratorio se han registrado como variables cuantitativas continuas. Las demás variables se han registrado como cualitativas. El riesgo coronario se ha calculado como variable cuantitativa continua y se ha dicotomizado como riesgo alto o no alto según el riesgo fuera >= 20% o < 20%.
Se ha realizado un análisis de regresión lineal entre cada par de ecuaciones para comprobar si hay relación entre los valores del riesgo calculado entre ellas.
Se ha calculado el coeficiente de correlación ordinal de Spearman entre cada par de ecuaciones para comprobar en qué medida los sujetos quedan ordenados de igual manera con una ecuación u otra.
Se ha calculado el coeficiente kappa de concordancia entre cada par de ecuaciones valorando el riesgo dicotomizado. También se ha valorado la concordancia mediante el coeficiente kappa entre los percentiles calculados con las correspondientes ecuaciones.
El análisis estadístico se realizó con el software SPSS 10.0.
Resultados
Se ha incluido en el estudio a 514 sujetos de 20 a 79 años, de los que 250 son varones (48,6%) y 264, mujeres (51,4%). La prevalencia de hipertensión arterial fue del 36,6%; la de hipercolesterolemia fue del 27,1%; la de diabetes, del 8,6%, y la de tabaquismo, del 33,9%.
Han tenido eventos vasculares previos el 6,6% de los varones y el 2,4% de las mujeres; se excluyó a estos sujetos del posterior análisis del cálculo de percentiles en prevención primaria. Se ha analizado a 464 sujetos en prevención primaria para ver la concordancia entre las ecuaciones.
En la muestra analizada, de las 240 mujeres, sólo el 2,5% llega a riesgo alto con la ecuación original de Framingham y ninguna tiene riesgo alto con las ecuaciones derivadas de los estudios REGICOR y DORICA; con esta última, los riesgos son superiores. De los varones, tiene alto riesgo el 29,5% con la ecuación original, el 8,5% con la ecuación del DORICA y el 2,2% con la ecuación del REGICOR.
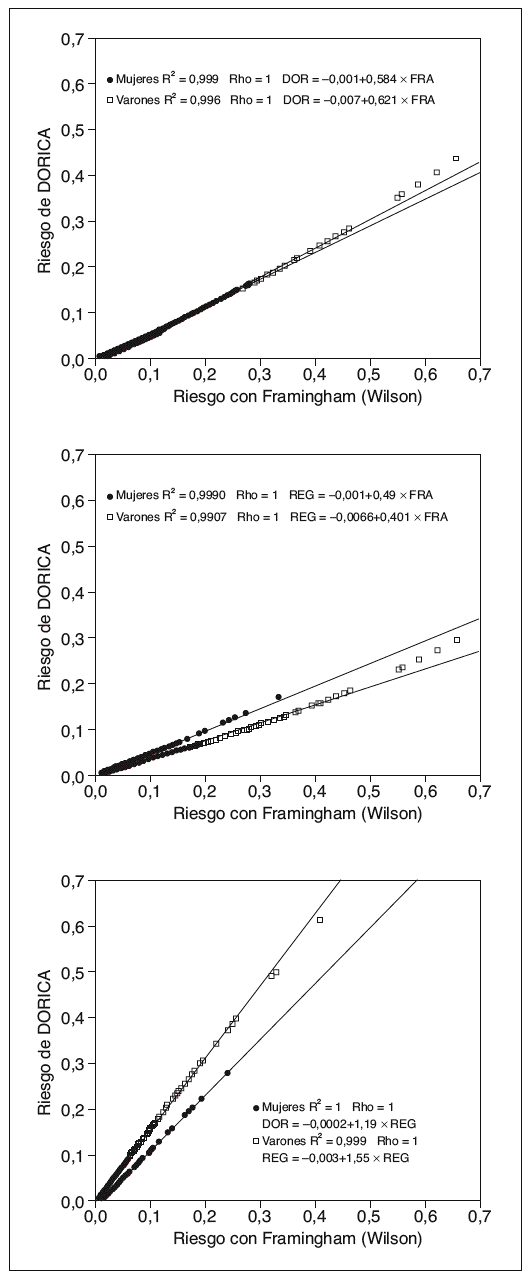
Se han calculado las correspondientes ecuaciones de regresión lineal entre cada par de ecuaciones de riesgo, tanto en varones como en mujeres, y se han apreciado unos coeficientes de correlación lineal muy altos, todos superiores a 0,995 (con r2 entre 0,9907 y 1). Estos resultados se pueden observar en la figura 1. Aproximadamente, el riesgo calculado con DORICA es el 60% del calculado con Framingham; el riesgo calculado con REGICOR es el 50% en las mujeres y el 40% en los varones respecto del calculado con Framingham; y el riesgo calculado con DORICA es 1,2 veces en mujeres y 1,5 veces en varones respecto del calculado con REGICOR.
Figura 1. Análisis de regresión lineal entre pares de modelos predictivos según el sexo con las ecuaciones de Wilson, DORICA Y REGICOR. Se presenta el cuadrado del coeficiente de regresión lineal r de Pearson, la ecuación de regresión y el coeficiente rho de regresión ordinal de Spearman para cada par de modelos. FRA: riesgo coronario con la ecuación de Framingham-Wilson; DOR: riesgo coronario con la ecuación de DORICA; REG: riesgo coronario con la ecuación de REGICOR.
También se han calculado los coeficientes de correlación ordinal de Spearman, cuyo resultado se aprecia en la misma figura 1. En las tres comparaciones, el coeficiente de correlación ordinal es 1, lo que demuestra que con cualquier ecuación los sujetos quedan en el mismo orden en cuanto a su riesgo, es decir, cualquier sujeto que por una ecuación tenga un riesgo superior a cualquier otro también será superior con cualquiera de las otras ecuaciones.
El resultado del análisis de concordancia entre las distintas ecuaciones cuando su resultado se dicotomiza como riesgo alto o no alto ofrece unos resultados diferentes según el par de ecuaciones seleccionadas y el sexo. En el caso de las mujeres, al haber sólo mujeres con riesgo alto con la ecuación original, cuando se analiza la concordancia entre ésta y cualquiera de las otras dos la concordancia es nula. La concordancia entre las dos calibraciones es máxima, ya que todas las mujeres tienen riesgo no alto. Cuando se analiza a los varones, la concordancia entre la ecuación de Framingham y la del DORICA es baja, con un índice kappa de 0,36. Menor es la concordancia de la ecuación original de Framingham con la calibración del REGICOR, ya que el índice kappa es 0,10. El índice kappa entre las dos calibraciones españolas es de 0,39. Si consideramos el conjunto de la muestra de varones y mujeres, los índices kappa correspondientes son 0,34, 0,08 y 0,35, respectivamente, como se aprecia en la tabla 1.
Cuando calculamos el índice kappa entre los percentiles calculados con cualquier par de ecuaciones, el resultado es máximo: hay una concordancia perfecta entre los percentiles de cualquier par de ecuaciones, como se aprecia en la tabla 1.
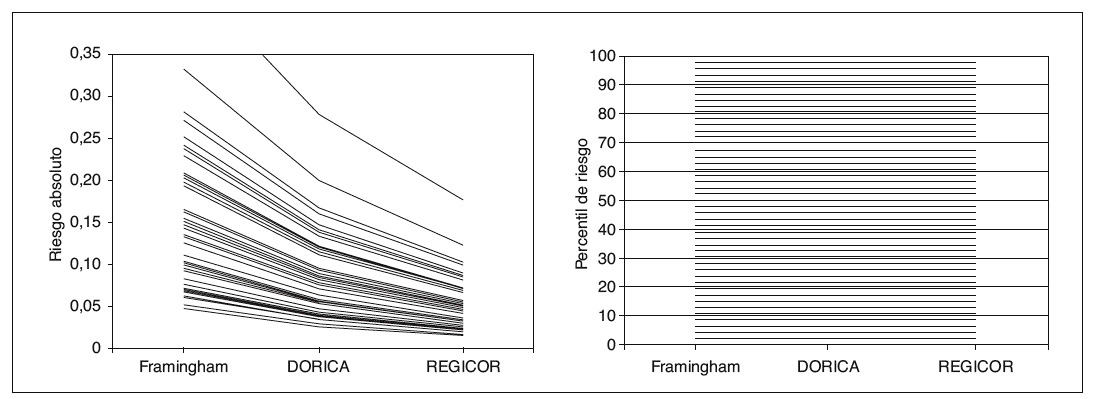
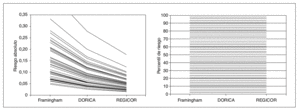
Figura 2. A la izquierda se representa el cambio en el riesgo coronario absoluto en cada varón de 55 a 64 años con las ecuaciones de Wilson, DORICA y REGICOR. A la derecha se representa el cambio en el percentil de riesgo coronario en los mismos sujetos con las ecuaciones de Wilson, DORICA y REGICOR. Cada línea representa a un sujeto de dicha edad.
Este comportamiento diferente en la concordancia según utilicemos el riesgo absoluto o el percentil se puede entender y comprobar gráficamente. En la figura 2, como ejemplo, se puede apreciar el cambio importante en el riesgo absoluto según la ecuación utilizada en cada varón de 55 a 64 años de la muestra estudiada. Se puede comprobar que ningún par de líneas se cruza (no cambian su orden), pero sí cambia claramente el riesgo absoluto. En cambio, al comparar los percentiles, obtenemos líneas perfectamente horizontales ya que, al no cambiar el orden, los sujetos tienen el mismo percentil con cualquier ecuación. Esto mismo ocurre en ambos sexos y en todos los estratos de edad.
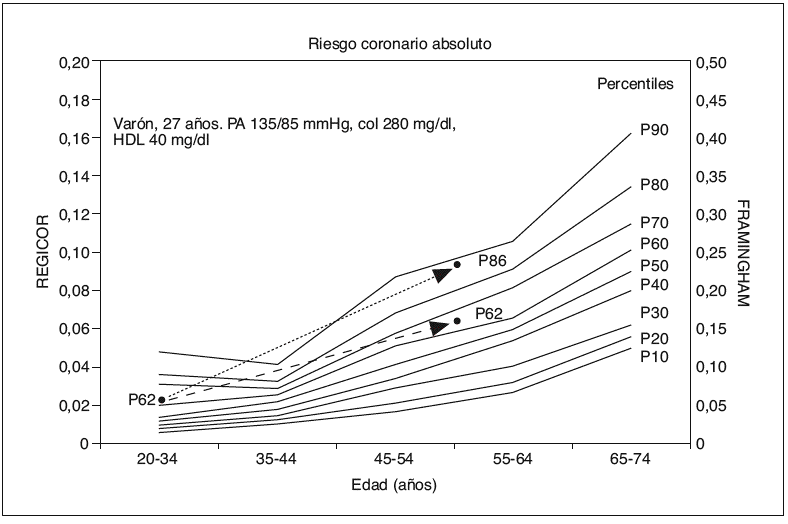
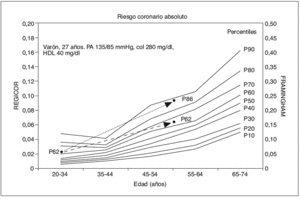
Una vez calculados los percentiles para cada sexo y grupo de edad, es posible la proyección del riesgo de los sujetos jóvenes a cualquier edad proyectando el percentil. En la figura 3 se puede comprobar la diferencia en el riesgo proyectado a los 60 años de un sujeto joven, según se proyecte sólo la edad o se proyecte el percentil. Cuando se proyecta la edad a los 60 años, se está calculando el riesgo absoluto que un joven tendría a la edad de 60 años si mantiene constantes todos sus factores de riesgo. Si se proyecta el percentil a los 60 años, suponemos que los valores de los distintos factores de riesgo van a cambiar con los años como sucede en el resto de sus coetáneos manteniendo su percentil; podremos calcular el riesgo a los 60 años que tendría si se mantiene en su percentil y comprobar que este riesgo es diferente del proyectado directa y exclusivamente con la edad. En el ejemplo de la figura, un varón de 27 años, con una presión arterial de 135/85 mmHg, un colesterol total de 280 mg/dl y un cHDL de 40 mg/dl tiene un riesgo absoluto según la ecuación de REGICOR del 2,2% (un 5,5%, según Framingham), que corresponde a un percentil 62. Si proyectamos su edad a los 60 años, su riesgo proyectado es del 9,8% (el 24,5% con Framingham), lo que constituye un percentil 86, mientras que, si conservamos su percentil 62, el riesgo proyectado es del 6,8% (el 17% con Framingham).
Figura 3. Gráfica de percentiles para varones según la edad. Se representa un ejemplo de proyección de un varón de 27 años no fumador a los 60 años mediante la proyección de la edad o mediante la proyección del percentil. Cuando se proyecta sólo la edad, se supone que los demás factores de riesgo no cambian. Cuando se proyecta el percentil, se supone que la evolución de los factores de riesgo es la que tenga la población de la que procede el sujeto. Se puede observar que el riesgo coronario proyectado es claramente diferente de un método a otro.
Discusión
La validez externa del presente trabajo reside en que se trata de un estudio basado en población general de la que se ha extraído una muestra mediante números aleatorios, a diferencia de otros trabajos de estudio de concordancia en los que se analiza una muestra consecutiva de pacientes atendidos en la consulta general o una muestra de sujetos con determinada enfermedad cardiovascular14. Esta validez respalda la aplicabilidad práctica del método expuesto en la población general.
El estudio epidemiológico de Framingham es el estudio más importante del mundo en el que se haya obtenido ecuaciones de predicción de riesgo cardiovascular. Pero la aplicabilidad a poblaciones diferentes de la original obliga a adaptar o validar dichas ecuaciones. Estas adaptaciones se han realizado en múltiples poblaciones15-17. En España se han adaptado estas ecuaciones mediante dos estudios diferentes, aunque mediante un sistema de calibración similar. Estos estudios son el REGICOR4 y el DORICA5. El REGICOR se basa en los datos del registro gerundense del corazón y el DORICA se basa en datos procedentes de varias regiones españolas. Dichos estudios han dado ecuaciones diferentes con cierto grado de acuerdo o desacuerdo, y el presente estudio es el primero que aporta una fórmula de equivalencia entre unas ecuaciones y otras con un muy alto índice de correlación. Pero además, el presente estudio aporta otra novedad aún más importante: la presentación de los percentiles como alternativa a múltiples ecuaciones o calibraciones, haciendo hincapié en el percentil y no en el riesgo absoluto como forma de adaptar las ecuaciones o como indicador de riesgo alto o bajo.
Nuestro trabajo es el primero que compara la concordancia entre las tres ecuaciones utilizadas. Se ha publicado un trabajo que estudia la concordancia entre las ecuaciones de Framingham originales (en su versión de Wilson, como en nuestro caso) y la calibrada de REGICOR con una base también poblacional18. Con los datos expuestos en dicho trabajo, aunque su análisis es diferente del realizado en el presente trabajo, se puede calcular el coeficiente kappa de concordancia en la clasificación alto o no alto riesgo entre ambas ecuaciones aplicadas a la muestra total de varones y mujeres, que fue 0,141. Dicho coeficiente es muy bajo y similar al obtenido en nuestro trabajo, que ha sido 0,083. Este resultado, obtenido por un equipo independiente del nuestro, respalda firmemente nuestros resultados y refuerza la validez externa del presente trabajo.
Otro trabajo publicado recientemente14 compara las ecuaciones de Wilson y REGICOR, y obtiene una concordancia baja para la clasificación de riesgo alto, con un índice kappa de 0,07. Aunque la muestra estudiada consiste en pacientes dislipémicos consecutivos atendidos en una consulta, este resultado también es similar al aquí presentado.
Es conocido que las ecuaciones que derivan directamente del estudio de Framingham sobreestiman el riesgo absoluto en nuestra población, por lo que es preciso calibrar dichas ecuaciones. Las ecuaciones derivadas del estudio REGICOR, que son una calibración de las originales, son más adecuadas a nuestra población, pero es llamativa la baja proporción de sujetos con alto riesgo cardiovascular en nuestro medio (un 2,2% de los varones), por lo que es posible que subestimen el riesgo. La última calibración española ha sido la procedente del estudio DORICA y, como podemos ver en nuestros resultados y en las gráficas presentadas, ofrece un riesgo intermedio entre la original y la del REGICOR. No obstante, no podemos todavía conocer cuál de las dos es más acertada en nuestra población.
Cuando el parámetro estadístico que medimos no es el riesgo absoluto sino su percentil, el panorama cambia radicalmente. La concordancia entre cualquier par de ecuaciones (Framingham, REGICOR o DORICA), tanto en varones como en mujeres, es pobre, pero la concordancia de los percentiles es total. Por lo tanto, puede ser más correcto calcular el percentil a un sujeto que calcular su riesgo absoluto. La limitación inicial de los percentiles es que no hay un percentil que defina lo que es riesgo alto o bajo. Pero esta limitación es relativa. El percentil alto lo determinará la morbimortalidad por enfermedad cadiovascular que tenga cada población. Así, no es tan importante si el riesgo es superior al 20% o no, sino si el percentil de un sujeto es superior al percentil determinado por la incidencia en su población coetánea de enfermedad cardiovascular. Cuando en una población se determina la incidencia de enfermedad cardiovascular, se puede determinar el percentil que indique riesgo alto, y entonces será de menor importancia escoger la ecuación original o una calibración u otra porque cualquiera dará lugar al mismo percentil.
Utilizar las ecuaciones originales o las calibradas y tomar el riesgo absoluto como medida del riesgo tiene inconvenientes muy importantes. El primer inconveniente es que cualquier ecuación hay que calibrarla si la población de origen es diferente de la población a la que queremos aplicarla. En España ya tenemos dos ecuaciones calibradas y no sabemos cuál es la idónea. Pero otro problema mayor es la elección del punto de corte que define riesgo alto. Se ha admitido por consenso que el punto de corte es el 20% (con las ecuaciones basadas en el estudio de Framingham como las que se ha emplea do en este trabajo), a partir del cual las diferentes guías y consensos aplican medidas de intervención en prevención cardiovascular más exigentes (con el sistema SCORE3 europeo, el punto de corte es el 5%, ya que sólo mide mortalidad cardiovascular y no morbimortalidad coronaria). Pero este punto de corte es cuestionable, ya que puede depender de la mayor morbimortalidad cardiovascular de la población, la disponibilidad de recursos económicos u otros factores. Así, en el Reino Unido el punto de corte seleccionado es el 30%19. También en nuestro medio se ha estimado la proporción de sujetos en riesgo alto según el punto de corte elegido con las ecuaciones del REGICOR20 o la proporción de sujetos no diabéticos candidatos a tratamiento hipolipemiante según el punto de corte18.
Otro problema importante es la limitación del intervalo de edad en que se puede aplicar la ecuación. Cada ecuación tiene un intervalo diferente. En el estudio de Framingham, el intervalo es el de 30 a 74 años y en el proyecto SCORE, de 40 a 65 años. Si aplicamos las ecuaciones fuera de su intervalo, se puede sobreestimar o subestimar el riesgo. Este inconveniente se puede paliar al menos en parte mediante la aplicación de los percentiles, ya que si utilizamos los percentiles la sobrestimación o subestimación del riesgo absoluto se produciría en todos los sujetos de la misma edad, por lo que los percentiles se verían poco o nada afectados.
Una tercera limitación importante es la utilización del riesgo absoluto en los sujetos jóvenes, ya que éstos no alcanzan riesgo alto con las ecuaciones. Para compensar la posible subestimación del riesgo en jóvenes, se ha propuesto dos soluciones diferentes. La primera es la utilización del riesgo relativo6, pero esta solución carece de puntos definitorios claros de riesgo alto. La otra solución es la proyección de la edad a los 60 años6,9. Esta solución tampoco es correcta, ya que al proyectar la edad se está asumiendo que los demás factores no cambian, lo cual sabemos que es falso: la presión arterial, el colesterol, etc., cambian con la edad. Además, elegir los 60 años para la proyección se basa en consensos. Con los percentiles proponemos una solución diferente: o establecemos unos percentiles definitorios de riesgo alto en los jóvenes o proyectamos su percentil a una edad determinada, con lo que suponemos que el sujeto se comportará como sus coetáneos, es decir, cambiará su presión arterial y su colesterol como lo hacen sus congéneres. Esta suposición es más plausible que suponer que no van a cambiar los factores de riesgo con la edad.
La aplicación de los percentiles exige ver los métodos de valoración del riesgo cardiovascular desde otra perspectiva. Siguiendo una analogía deportiva, las medallas en una carrera no se dan a los que superen cierta marca absoluta, sino a los que corran más rápido. Es el percentil y no la medida absoluta lo que determina quién gana o pierde, independientemente de que el cronómetro del comisario esté adelantado o retrasado.
Podemos concluir que la utilización de los percentiles abre una nueva puerta de valoración del riesgo cardiovascular en la que se descubre un nuevo camino que seguir: hay que realizar estudios epidemiológicos de riesgo cardiovascular para conocer la realidad de la enfermedad cardiovascular, determinar los percentiles de riesgo y establecer nuevas instrucciones operativas en cada población. El camino sería no tanto cuál es la ecuación mejor, sino cuál es la morbimortalidad poblacional. Los percentiles se pueden aplicar a cualquier ecuación de riesgo cardiovascular basada en cualquier modelo matemático.
Grupo ERVPA (Estudio de Riesgo Vascular de Palencia)
Complejo Hospitalario de Palencia, Servicio de Medicina Interna: José Ignacio Cuende Melero; Hospital Universitario del Río Hortega de Valladolid, Sección de Nefrología: Alfredo Acebal Botín; C.S. de Frómista: Amalia Durántez Nevares, Andrés Sánchez Bosch, Alejandro Suárez Fernández, Priscila García García, Eduardo Useros Fernández, M. Luz Hermoso Elices, Lourdes Sanz Gaite, Pilar Abarquero Coloma, Jesús M. Triana Sánchez; C.S. de Villarramiel: Roberto Jiménez Gómez, Rafael Magdaleno Pérez, Francisca Capa Espejo, Florentino Salado Cuadrado, Gladys Hurtarte Cabrera, M. Milagros Zoreda Aguado, Ángel de Miguel Gutiérrez, M. Vega Panedas Gómez; C.S. de Torquemada: M. Victoria Bertolín Burillo, Santiago García Millán, M. Concepción Mancebo Allende, Manuel I. Corral Moro, Miguel A. Martínez Flores, M. Irene Pardo García, Javier Romero Cristóbal, Ángela García Santos; C.S. de Baltanás: Esperanza Fernández González, Margarita González; C.S. de Paredes de Nava: Fernando Sánchez García, Carlos Flores Farrán, Juan Ignacio Gutiérrez Díez, Ángela Báscones Cobb, Ismael Blanco Urzáiz; C.S. de Jardinillos y La Puebla: Luis Jolín Garijo, Azucena Carrera Camarón, M. Dolores Pérez Lezcano, Ana Marcos Rodríguez, María Redondo Valdeolmillos, Mercedes Durántez Cacharro; C.S. de Herrera de Pisuerga: Enrique Conde del Teso, M. del Valle Alaiz Poza, Isaac Villalba, Pilar García Medina, M. Felipa Pedroso Gutiérrez, Sol González Gago, José Ignacio de la Fuente, Rosa María González, Juan M. Cacharro; C.S. de Saldaña: José Donis Domeque, Juan Carlos Luppi Bustillo, Alicia Fernández Nieto, Nélida García Vallejo, José Álvarez López, Antonio Martín Bueno, Jesús María Díez Ruiz, Francisco Díez Cordero, María Muelas García y José Luis Abad Fernández.