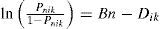Difficulties of items related to energy and matter: Implications for learning progression in high school chemistry

Abstract

Understanding the development of high school students’ ideas and ways of reasoning about matter and energy is of central importance to foster meaningful learning in chemistry courses. Similarly it is critical to investigate student understanding of models and modeling. In this work, we used computer model-based assessment questions to investigate student understanding of: a) matter and energy, and b) models and modeling, in the context of nine different chemistry topics. The comparison of item difficulty across topics allowed us to elicit a possible learning progression for high school chemistry. The results of our study can inform the development of secondary school chemistry curricula.

Resumen

La comprensión de cómo se desarrollan las ideas y las formas de razonamiento de los estudiantes sobre los conceptos de materia y energía es de central importancia para favorecer el aprendizaje significativo en cursos de química. Es también crítico investigar la comprensión de los estudiantes sobre modelos y modelaje. En este trabajo utilizamos preguntas de evaluación basadas en modelos computacionales para investigar la comprensión de los estudiantes sobre: a) materia y energía, y b) modelos y modelaje, en el contexto de nueve temas diferentes de química. La comparación del nivel de dificultad de preguntas sobre diferentes temas nos permitió hacer visible una posible progresión de aprendizaje sobre temas de química en el bachillerato. Los resultados de nuestro estudio pueden informar el desarrollo de currículos de química en ese nivel educativo.

Introduction

There have been many advances in chemical education research in recent years; among them we find two promising approaches that can potentially transform how student learn chemistry: a) computer models and modeling, and b) learning progressions. There is overwhelming evidence that computer models and modeling facilitate students’ understanding of chemical concepts (Ardac & Akaygun, 2004; Chang et al., 2010; Dori & Sasson, 2008; Doymus et al., 2010; Frailich et al., 2009; Ozmen, 2011; Plass et al., 2012; Scalise et al., 2011; Shen et al., 2011; Snir et al., 2003; Stieff, 2004; Talib et al., 2005). For example, in a literature review of 61 empirical studies over the last decade, Smetana and Bell (2012)found that computer simulations can be as effective, and in many ways more effective, than traditional instructional practices (e.g., lecture-based, textbook-based, and/or physical hands-on) in promoting student knowledge acquisition, developing process skills, and facilitating conceptual change. In a similar synthesis of the research literature in the last decade, Rutten et al. (2012)found that there is robust evidence that computer simulations can enhance traditional instruction. Computer models and modeling can promote student scientific exploration, facilitate model-based reasoning (e.g., qualitative and quantitative thinking, systems thinking, and computational thinking habits), and enhance collaborative learning (Shen et al., 2011).

Recently, the concept of learning progression has been promoted as a useful tool for organizing science curricula and conducting science instruction (NRC, 2007), and it has informed the development of the next generation science education standards (NRC, 2012; Achieve, 2013). While a number of tentative learning progressions have been developed in different areas (e.g., Alonzo & Steedle, 2009; Duncan et al., 2009; Jin & Anderson, 2012; Songer et al., 2009), little empirical research is available on a learning progression for high school chemistry. When examining the sequence of chemistry topics taught in secondary schools, we may find various orders, which suggests that there is not a commonly agreed upon curricular sequence. Experienced chemistry teachers using the same textbook may decide to follow a different sequence of topics for various valid reasons, and often these reasons are not explicitly articulated to new and more inexperienced teachers. Consequently, there is a need in chemical education research to articulate a learning progression for high school chemistry.

In order to develop such a learning progression, we first need a rationale or framework for the progression of core concepts and ideas. Fostering the development of chemical reasoning can be a powerful way to approach this task. We can conceptualize chemical reasoning as consisting of two main dimensions: understanding of matter, energy, and their interactions, and understanding of models. Matter and energy are foundational for chemistry. Chemistry is the study of the structure, composition, and changes of matter, where the concept of energy serves as a mathematical account for stability and transformation. A combined matter and energy approach to studying chemistry provides a systematic view of the material world; it represents how experts approach questions related to the physical world. This systematic way of thinking was better described by Feynman in one of his well-known lectures, Atoms in Motion (Feynman, 1963). Using a water drop as an example, Feynman explained how various chemistry concepts and ideas, including kinetic molecular theory, structure of matter, evaporation and condensation, chemical change, physical change, and so on, are the result of our systematic imagination and thinking about the world. In the same way that we can use our imagination to envision “the whole universe is in a glass of wine” (Feynman, 1963, p. 66), we can find all chemistry within a single natural phenomenon. This systematic approach to the study of matter demands finding the answer to the following essential questions: How does matter exist? How can we classify it? What is its structure? How does it change chemically? How does it change physically? The answer to these questions requires the understanding of states of matter, classification of matter, atomic structure, chemical bonding, and intermolecular forces. Similarly, systematic thinking about energy demands the answer to the following questions: What is the form of energy? How can it be transferred? What is lost during transfer? How is it conserved? The answers to these questions involve the understanding of forms of energy, energy transfer, energy degradation, and energy conservation. Together, the above questions serve as a guide for systematically thinking about matter and its changes.

Using items designed specifically to measure high school chemistry students’ understanding of matter and energy within the context of computer models and modeling, the present study was designed to answer the following questions:

• 1.

  What are the difficulty levels of items designed to measure students’ understanding of matter and energy in the context of various high school chemistry topics? Is there a significant difference in the average difficulty of items addressing different chemistry topics?

• 2.

  How are the difficulty levels of items designed to measure students’ understanding of models and modeling in the context of various high school chemistry topics? Is there a significant difference in the average difficulty of items addressing different chemistry topics?

• 3.

  Is there a significant interaction effect between the above mean difficulties of items for matter and energy and models and modeling?

The answers to these questions can advance our knowledge and understanding about students’ development of the core concepts: matter, energy, and models. Such answers have critical implications for a learning progression within a high school chemistry course.

Method

Data for this study came from a project called Connected Chemistry as Formative Assessment (CCFA) funded by the National Science Foundation (please refer to Liu et al., 2012; Waight et al., 2013 for more information). CCFA integrates formative assessment, computer models and modeling, and learning progression. The development of assessment items followed the construct modeling approach (Wilson, 2005). Progress variables on matter, energy, and models were conceptualized to consist of three levels. Table 1 presents the different levels within each of the progress variables associated with these core concepts.

Table 1.

Levels of Understanding of Matter-Energy and Models.

	Matter-Energy	Models
Level 1	Describes that matter exists in different states and has various types, and that different states and types of matter are associated with different forms of energy	Uses models for literal illustration of a single phenomenon
Level 2	Explains chemical properties using structural theories of matter (atomic structure and bonding theories) and energy transfer	Uses models to depict a range of phenomena
Level 3	Explains physical properties by considering the whole system that is characterized by interactions among particles (e.g., intermolecular forces), entropy, and energy conservation	Uses models as tools to make predictions and test hypotheses

Students’ behaviors on each of the progress variables were solicited by computer model-based assessment questions. That is, students first interacted with a computer model, and then answered questions related to specific aspects of the model. Computer model-based assessments on matter, energy, and models were developed for the following nine commonly taught topics in a high school chemistry course: Atomic Structure, States of Matter, Solutions, Gases, Stoichiometry, Chemical Bonding, Chemical Equilibrium, Redox, and Acids and Bases. The topic of periodic properties was dropped due to lack of items fitting the Rasch model (described below). Each assessment included at least one Flash animation, one NetLogo model, and a set of assessment questions. Assessment questions were in the format of Ordered Multiple-Choice (OMC) (Briggs et al., 2006), with answer choices matching different levels of a progress variable (all computer models are available at http://wings.buffalo.edu/research/ConnectedChemistry/).

The following sample questions are illustrative of the items used when students worked with computer models for the topic of States of Matter:

Sample Matter Question: Which of the following statements best describes the commonalities or differences among three phases of the substance in the container?

• a.

  The substance in different phases has the same composition. (level 1)

• b.

  The chemical bonds of the substance in different phases are the same. (level 2)

• c.

  The intermolecular forces in different phases are different. (level 3)

Sample Energy Question: In the temperature-energy diagram, which of the following best describes why the two horizontal lines have different lengths?

• a.

  They represent different amounts of energy. (level 1)

• b.

  They represent different amounts of transferred energy. (level 2)

• c.

  They represent different processes of conserving energy. (level 3)

Sample Model Question: Which of the following statements best describes the white substance in the container?

• a.

  ice at the room temperature. (level 1)

• b.

  a solid substance at the room temperature. (level 2)

• c.

  any solid substance of my choice. (level 3)

The initial versions of the computer models and assessments were pilot-tested with one group of students during the academic year 2009-2010 (n = 15-25). Three individuals with expertise in chemistry, psychometrics, and science assessment reviewed these initial versions. The revised models and assessments were then field-tested in two high school chemistry classes in two schools during the academic year 2010-2011. Based on data collected during the year, further revisions to the questions were made. An extended field-testing of the assessments was conducted during the academic year 2011-2012. Ten chemistry teachers from 10 schools participated in the extended field-testing. During the year, each of the 10 teachers incorporated the computer models and computer-model based assessments into at least one of his/her chemistry classes.

Students’ responses to the nine computer model-based assessments were analyzed using the Rasch model. Rasch measurement is based on an equation originally developed by a Danish mathematician named George Rasch (Rasch, 1960/1980). We used the partial credit Rasch model (Masters, 1982), which takes the following form:

where P_nik is the probability for student n with an ability Bn responding successfully at level k instead of level k - 1 to item i;. D_ik is the difficulty of level k of item i.

Although matter and energy are conceptually distinct concepts in chemistry, previous Rasch analysis indicated that they are psychometrically highly correlated and can be treated as one dimension. A combined matter and energy dimension is consistent with our emphasis on systematic thinking about a chemical system. The conceptual framework for next generation science standards also includes “energy and matter - flows, cycles, and conservation” as one of the crosscutting concepts in science and engineering. Multi-dimensional Rasch models, specifically the Multidimensional Random Coefficients Multinomial Logit (MRCML) model (Adams et al., 1997), together with Con-Quest computer software (Wu et al., 1997) were used for the above analysis.

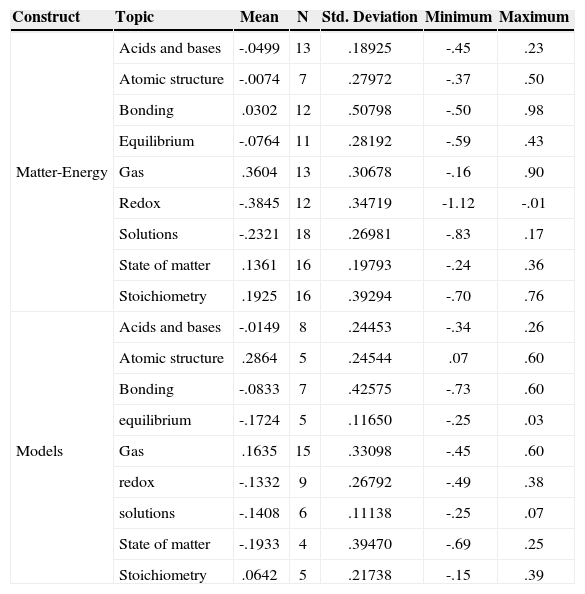
Results

In Rasch analysis, item difficulty is measured in a logarithm unit defined as the natural logarithm of the odds of answering a question at one level over the probability for answering a question at a lower level. This unit is also called logit. The more positive the logit value for a question, the higher its difficulty. Logit measures are interval, and can be transformed linearly to a scale with any mean and standard deviation. Table 2 presents descriptive statistics of item difficulties related to different chemistry topics.

Table 2.

Descriptive Statistics of Item Difficulties.

Construct	Topic	Mean	N	Std. Deviation	Minimum	Maximum
Matter-Energy	Acids and bases	-.0499	13	.18925	-.45	.23
	Atomic structure	-.0074	7	.27972	-.37	.50
	Bonding	.0302	12	.50798	-.50	.98
	Equilibrium	-.0764	11	.28192	-.59	.43
	Gas	.3604	13	.30678	-.16	.90
	Redox	-.3845	12	.34719	-1.12	-.01
	Solutions	-.2321	18	.26981	-.83	.17
	State of matter	.1361	16	.19793	-.24	.36
	Stoichiometry	.1925	16	.39294	-.70	.76
Models	Acids and bases	-.0149	8	.24453	-.34	.26
	Atomic structure	.2864	5	.24544	.07	.60
	Bonding	-.0833	7	.42575	-.73	.60
	equilibrium	-.1724	5	.11650	-.25	.03
	Gas	.1635	15	.33098	-.45	.60
	redox	-.1332	9	.26792	-.49	.38
	solutions	-.1408	6	.11138	-.25	.07
	State of matter	-.1933	4	.39470	-.69	.25
	Stoichiometry	.0642	5	.21738	-.15	.39

Data in Table 2 indicates that, for the matter-energy construct, items related to the topic of Gases had the highest mean difficulty, while items in the Redox category had the lowest mean difficulty. We can also note that difficulties among items within the same topic also varied, with the greatest variation associated with questions about bonding (sd = 0.50). For the model construct, items in the Bonding category had the highest mean difficulty, while items about states of matter had the lowest mean difficulty. Similarly, there was a variation in difficulty among items within a given topic, with the greatest variation associated with questions about chemical bonding (sd = 0.43).

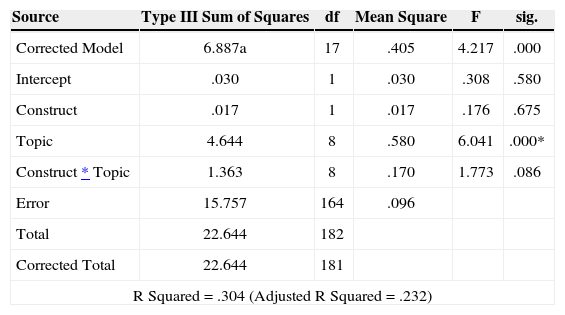
A two-way analysis of variance on item difficulties using topics (e.g., Gases, Bonding) and construct (e.g., Matter-Energy Models) as independent variables found that there was no topic by construct interaction effect. Differences in item difficulties were mainly linked to the nature of the topic, and not to the nature of the construct. Table 3 presents the quantitative data that supports these results.

Table 3.

Analysis of Variance by Construct and Topic.

Source	Type III Sum of Squares	df	Mean Square	F	sig.
Corrected Model	6.887a	17	.405	4.217	.000
Intercept	.030	1	.030	.308	.580
Construct	.017	1	.017	.176	.675
Topic	4.644	8	.580	6.041	.000*
Construct * Topic	1.363	8	.170	1.773	.086
Error	15.757	164	.096
Total	22.644	182
Corrected Total	22.644	181
R Squared = .304 (Adjusted R Squared = .232)

*

p<.05

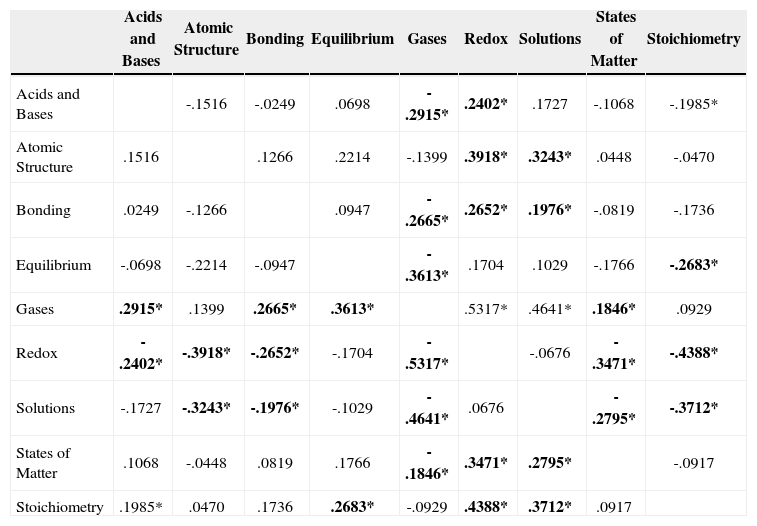
Post-hoc comparison using a liberal method, i.e., Fisher’s Least Significant Difference (LSD), indicated the following statistically significant differences in the mean difficulty of items associated with different pairs of topics:

• —

  Acids and Bases when compared with Gases, Redox, or Stoichiometry;

• —

  Atomic Structure when compared with Redox or Solutions;

• —

  Bonding when compared with Gases, Redox, or Solutions;

• —

  Equilibrium when compared with Gases or Stoichiometry;

• —

  Gases when compared with Acids and Bases, Bonding, Equilibrium, Redox, Solutions, or States of Matter;

• —

  Redox when compared with Acids and Bases, Atomic Structure, Bonding, Gases, States of Matter, or Stoichiometry;

• —

  Solutions when compared with Atomic Structure, Bonding, Gases, States of Matter, or Stoichiometry;

• —

  States of Matter when compared with Gases, Redox, and Solutions;

• —

  Stoichiometry when compared with Acids and Bases, Equilibrium, Redox, and Solutions.

Table 4 presents the quantitative data associated with these different pair-wise comparisons.

Table 4.

Mean difference in item difficulty for questions sets corresponding to two different topics. Numbers in bold correspond to statistically significant differences (p*<.05). A positive (negative) number indicates that items for the topic in a given row were more (less) difficult than the items in a selected column.

	Acids and Bases	Atomic Structure	Bonding	Equilibrium	Gases	Redox	Solutions	States of Matter	Stoichiometry
Acids and Bases		-.1516	-.0249	.0698	-.2915*	.2402*	.1727	-.1068	-.1985*
Atomic Structure	.1516		.1266	.2214	-.1399	.3918*	.3243*	.0448	-.0470
Bonding	.0249	-.1266		.0947	-.2665*	.2652*	.1976*	-.0819	-.1736
Equilibrium	-.0698	-.2214	-.0947		-.3613*	.1704	.1029	-.1766	-.2683*
Gases	.2915*	.1399	.2665*	.3613*		.5317*	.4641*	.1846*	.0929
Redox	-.2402*	-.3918*	-.2652*	-.1704	-.5317*		-.0676	-.3471*	-.4388*
Solutions	-.1727	-.3243*	-.1976*	-.1029	-.4641*	.0676		-.2795*	-.3712*
States of Matter	.1068	-.0448	.0819	.1766	-.1846*	.3471*	.2795*		-.0917
Stoichiometry	.1985*	.0470	.1736	.2683*	-.0929	.4388*	.3712*	.0917

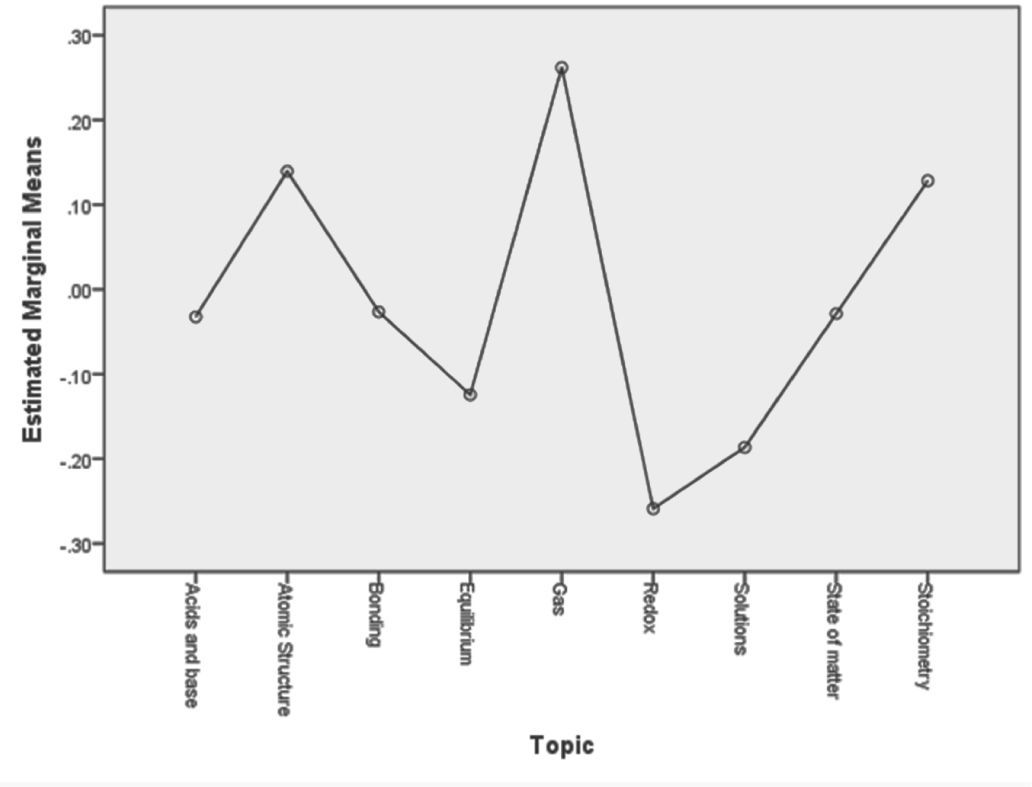
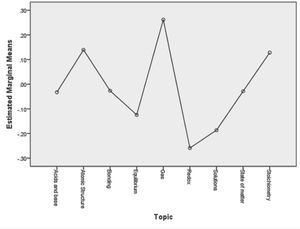
Figure 1 plots the marginal item difficulty means for all items within a given topic. Based on this data, topics can be arranged into the following four clusters from most difficult to least difficult: (a) Gases, (b) Atomic Structure and Stoichiometry, (c) Acids and Bases, Bonding, and States of Matter, and (d) Equilibrium, Solutions, and Redox.

Figure 1.

Mean difficulties of items on matter-energy and models among nine chemistry topics.

Discussion

Learning progressions are “descriptions of the successively more sophisticated ways of thinking about a topic that can follow one another as children learn about and investigate a topic over a broad span of time” (NRC, 2007, p. 219). If we assume that differences in item difficulty correspond to differences in levels of sophistication in the ways of thinking about various chemistry topics, then the results presented in the previous section may suggest a possible learning progression. This progression would move from understanding chemical equilibrium, solutions, and redox reactions to understanding acids and bases, chemical bonding, and states of matter, to understanding atomic structure and stoichiometry, to finally understanding gases.

To make sense of the suggested learning progression for high school chemistry, we need to think about potential reasons for such a progression. Research in science education suggests that student development of sophisticated ideas takes time and may involve many intermediate ways of thinking, some of them naive and based on misconceptions. Thus, a learning progression is to make learning “gradual” or “progressive” in the sense that later learning is built upon previous learning. This is what a spiral curriculum intends to achieve (Bruner, 1960). Specifically for chemistry teaching, Taber (2012) has emphasized the importance of building student understanding over time in a spiral format.

Previous research has suggested many different ways to foster learning. For example, Ausubel’s cognitive learning theory gives primary importance to developing new cognitive structures in learning from prior knowledge (Ausubel, 1968). Specifically, Ausubel suggested that an important mechanism for developing new cognitive structures is through integrative reconciliation. Contrary to progressive differentiation, integrative reconciliation involves building new learning based on commonalities or connections with existing knowledge, allowing for the introduction of more inclusive or broader concepts. Joseph Novak has operationalized integrative reconciliation and progressive differentiation into concept mapping (Novak & Gowin, 1984). More recently, various scholars have proposed the notion of curriculum coherence (AAAS, 2001; Schmidt et al., 2005) as an approach to support learning. A coherent curriculum is one that over time follows a sequence of topics and performances consistent with the logical and, if appropriate, hierarchical nature of the disciplinary content from which the subject-matter derives (Schmidt et al., 2005). For high school chemistry, the logic and hierarchy of reasoning may be demonstrated in the following ways: qualitative to quantitative, descriptive to predictive, observational to experimental, macroscopic to microscopic, experimental to computer modeling, and simple to complex.

Based on the above possible mechanisms of learning progression, the sequence of topics that emerged from the analysis of item difficulty in our work may respond to the following logic. First, from primarily qualitative to quantitative, as the most difficult topics, such as Stoichiometry and Gases, involve quantifications of substances and mathematical relationships between and among substances, while other topics may be primarily studied in qualitative ways. Second, the elicited sequence of topics can also be considered as following a logic from descriptive to predictive, as Atomic Structure, Chemical Bonding and Kinetic Molecular Theory (KMT) are theoretical models used to explain chemical equilibrium, solutions processes, redox reactions, and acid-base reactions. Finally, the topical sequence can be considered as following a logic from simple to complex because studying phase changes and gas behavior requires an understanding of not only structure and properties of individual particles (atoms, ions, and molecules) but also of interactions among many particles — a system view.

According to our results, the topic of Gases is the most difficult of all. This finding is consistent with previous research on students’ alternative conceptions about states of matter. Key understandings about gases in a high school chemistry course are based on the KMT and the notion of heat. Students of all ages, including high school and university students, have major difficulties understanding these concepts (Kind, 2004). For example, in one study involving 100 undergraduates, none of them attributed dye diffusion to random motion of particles (Westbrook & Marek, 1991). In a classic study on students’ alternative conceptions about matter, Novick and Nussbaum (1981)found that only about half of students aged 16 and above thought that particles in a flask were in constant motion. The existence of empty space between participles is another very difficult idea for high school or even university students to understand. In a study about heat and temperature (Lewis & Linn, 1994), no clear differences were found in the responses provided by 8^th grade students, adults (first-year chemistry college students, college staff assistants, lab technicians, college counselors and liberal arts faculty), and natural scientists (physicists and chemists). In that investigation, eighty percent of the middle school students responded that objects sitting in a room would be at a different temperature; adults stated that metals did not retain heat as well as other materials; and two scientists were either unwilling or unable to differentiate between heat and temperature.

The sequence of topics that emerged from our analysis is just one of many possible learning progressions a high school chemistry course may follow. Different learning progressions aim at developing different ideas foundational to chemistry. The sequence suggested in this study aims at developing student understanding about matter, energy and models; it is a promising way to conceptualize high school chemistry teaching and learning in today’s digital age.

Acknowledgement

The materials reported in this paper are based upon work supported by the National Science Foundation under Grant No. DRL-0918295.