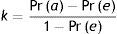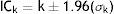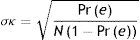Agradecemos los comentarios de Dominguez-Lara, a propósito de la relevancia de reportar los intervalos de confianza para el índice de concordancia kappa.
La estimación de la concordancia entre 2 observadores puede realizarse de distintas maneras. El método más básico es el recuento de los acuerdos, y dividirlo por el número total de observaciones, pero esta técnica no está teniendo en cuenta los aciertos consecuencia del azar. El indicador que tiene en cuenta las concordancias producto del azar es el propuesto por Cohen1 y denominado índice kappa (κ); que es el estadístico más utilizado para estos casos.
Al igual que ocurre con otros estadísticos, como los coeficientes de correlación de Pearson o Spearman, el valor obtenido en el índice de kappa (κ) es una estimación puntual, que se interpreta en función de una tablas de valores2. De tal forma, que cuanto más próximo a 1, mayor será el acuerdo entre los observadores, y cuanto más cercano a −1, menor será el acuerdo.
En nuestro caso, el valor obtenido de κ es de 0,371, lo que nos indica que el grado de concordancia fue entre débil y moderado. Si bien es cierto, que el cálculo de un intervalo de confianza permite establecer un rango de valores entre los que se mueve el verdadero valor con un cierto nivel de confianza, no se consideró adecuado su cálculo, teniendo en cuenta el bajo valor del índice κ obtenido.
Pero siguiendo la sugerencia del lector, hemos calculado el intervalo de confianza (IC) mediante las siguientes fórmulas:
Cálculo del estimador1:
dónde: Pr (a) es el acuerdo observado relativo entre los observadores (Pr [a]=43,75%); Pr (e) es la probabilidad hipotética de acuerdo por azar (Pr [e]=10,55%)Con estos datos, κ=0,3711
Comprobación de la significación del estadístico calculado:
Ho: el coeficiente de κ es igual a cero
H1: el coeficiente de κ es distinto de cero
El estadístico Z calculado ofrece un valor de 5,68 con un p-valor asociado (para un nivel de significación alfa=0,05) menor que 0,001. Por lo tanto, se rechaza la hipótesis nula, y podemos concluir que el coeficiente calculado es estadísticamente significativo3.
Cálculo del IC:
dónde: N=16; nivel de confianza: 95%; Pr (e)=10,55%De donde obtenemos que el IC 95%=0,2028; 0,5394
Por lo tanto, nuestro resultado es diferente al aportado por Dominguez-Lara, debido a que su cálculo de Fe no se corresponden con los resultados obtenidos por nosotros con el programa estadístico (Stata v.12) y confirmados mediante el cálculo manual.