Recently, several mathematical models have been developed to study and explain the way information is processed in the brain. The models published account for a myriad of perspectives from single neuron segments to neural networks, and lately, with the use of supercomputing facilities, to the study of whole environments of nuclei interacting for massive stimuli and processing. Some of the most complex neural structures -and also most studied- are basal ganglia nuclei in the brain; amongst which we can find the Neostriatum. Currently, just a few papers about high scale biological-based computational modeling of this region have been published. It has been demonstrated that the Basal Ganglia region contains functions related to learning and decision making based on rules of the action-selection type, which are of particular interest for the machine autonomous-learning field. This knowledge could be clearly transferred between areas of research. The present work proposes a model of information processing, by integrating knowledge generated from widely accepted experiments in both morphology and biophysics, through integrating theories such as the compartmental electrical model, the Rall’s cable equation, and the Hodking-Huxley particle potential regulations, among others. Additionally, the leaky integrator framework is incorporated in an adapted function. This was accomplished through a computational environment prepared for high scale neural simulation which delivers data output equivalent to that from the original model, and that can not only be analyzed as a Bayesian problem, but also successfully compared to the biological specimen.
Recientemente se han desarrollado modelos matemáticos que permiten explicar y definir a través de la ingeniería la manera como se procesa la información de señales eléctricas producidas por iones en el sistema nervioso de los seres vivos. Se han diseñado numerosas propuestas de este tipo de lo discreto a lo masivo, que operan como segmentos de una neurona, una red, y en últimas fechas con ayuda del supercómputo, hasta conjuntos de núcleos que interactúan en entornos de estímulos y procesamiento a gran escala. De las estructuras neurales más complejas y de más interés ha sido la del grupo denominado de los Ganglios Basales, de los que el Neoestriado forma parte, y sobre el cual se han hecho pocos trabajos de modelado computacional. Se ha demostrado que en esta región residen funciones de aprendizaje, y otras relacionadas con la toma de decisiones bajo las reglas de acción-selección que son ampliamente estudiadas en el aprendizaje autónomo computacional, permitiendo transferir el conocimiento de un campo de investigación a otro. El presente trabajo propone un modelo computacional en tiempo real, a través de integrar el conocimiento obtenido de experimentos ampliamente aceptados en biofísica, aplicando la teorías de compartimientos electrónicos, de la ecuación de cable de Rall, las leyes de potencial de partículas Hodkgin-Huxley, entre otros. Dichos modelos se incorporan en un entorno basado en la función de integrador con fugas, a través de un ambiente computacional de simulación neural a gran escala, que entrega una salida de datos equivalente al modelo biológico, susceptible a ser analizada como un problema Bayesiano, y comparada con el espécimen biológico con éxito.
In the past two decades, researchers have increasingly become interested in building computer simulations of diverse brain structures, based upon morphological and physiological data obtained from biological experimental procedures.
The efforts for building off these constructs are only directed by the findings in biological models, leading to specific algorithms [1, 2]. Thus, they are aimed to the creation of neural simulation platforms --yet specifically designed for suiting a particular characteristic from a given region [3] -- or for general purposes, demonstrating that many functions are present in specific regions of the nervous system and can be applied generally, and at the same time, they are also present among many species at many levels of differentiation [4].
All of these tools have been useful both, for consistently recreating the findings at different scenarios, and for welcoming new proposals and directing new experiments, or even to predict new findings in diverse brain structures [5, 6]. The use of this kind of methodologies have made possible the simulation of neural processes at many levels of detail, analyzing from membrane regions with ionic channels for simulating the effects of neuromodulation and neurotransmitter action in membrane potential, and building off a whole neuron with all the electrophysiological responses [7, 8], to a specific cell network [9, 10]. These algorithms and computational environments are only limited by the current state of art of their respective experimental procedures on the one side, and for the computing capacity on the other [11-13].
Many simulations of diverse regions and networks as well as analysis of several information processing strategies about how this neural network works, have been published elsewhere [14-17]. For supporting this research, plenty of tools for building real time simulations of diverse brain structures have been reported [18]; thus helping and directing the biological findings trough experiment-biological cycles and perfecting each other in every iteration [19]. Given this knowledge production for biophysics, there is understandable growing interest in computer engineering field, to study the information processing in living neural structures, because the so-called “Intelligent Planning and Motivated Action Selection” [20, 21], which is a task well characterized in animal behavior, and also a computational problem intensively studied in artificial intelligence field [22-24].
These particular properties of information processing and decision making have been discovered on some brain structures as the respective methodologies for their study have been developed, and the equipment needed for the experimental procedures has been perfected. In mammals, the specialized brain structures where this functions have been demonstrated -but not well understood- are the basal ganglia (BG), which are located in sub cortical brain region [25, 26]. BG structures are composed by several nuclei, from which neostriatum (NS) is widely accepted as the main input nucleus [27-29]. Although there is a lot of theoretical approach about the information processing form of this region, the construction of respective real time computer models and analysis are just emerging [10, 25, 30, 31].
From the perspective of computational ccience, “Reinforcement-Learning” [32], and “Action-Selection” theories [33] have been developed many decades ago as theory for machine learning strategies [20, 34]. Therefore, they have been associated to some of the functions of BG [35, 36] and more specifically within the activity of NS [37,38]. However, related to this nucleus, only a few dynamical systems in real time have been built allowing integration, comparing and testing the experiences and data acquired from biological models to computational ones [39,40].
The present work extends the use of these methodologies, through the use of a general purpose neural simulator [41, 42] in a high demand computational environment, which served for building a simplified model of NS composed of mathematical models for the best characterized cell types, -- the main output neuron is one of them, organized in regions and delimited by the interconnection of their respective inter- neurons [43, 44]-. This whole structure was added with both excitatory external signaling and bi-modal modulation as inputs, assembling the functions of cerebral cortex and thalamus effect on the NS on one side, and dopaminergic (DA) effect on the other [45, 46]. All this model was strictly built based on morphological and physiological data reported from classical experiments reviewed in biological reports [47-49].
The output data of the model was processed and analyzed qualitatively against the biophysical experiments, and quantitatively by the same component current/voltage analysis methodologies which were used for characterizing separately each ionic currently studied in electrophysiology [50, 51], as is discussed in the results section.
2Neostriatum, Anatomy and FunctionThe anatomical and physiological data which form the basis of our model are well known, and are described in several reviews [43-45, 52]. Their function has been conceptualized as four nuclei that process information from the cerebral cortex related to the pathway regarding movement, posture and behavioral responses [53]. Initially BG function was associated to movement execution and feedback control [54, 55], this is because the first knowledge of BG was a condition known as “Parkinson Disease” which clinically expresses an impairment of motor responses [56, 57, 58]. Actually, it is known that BG are also involved in the process of attention and decision making, as explained above.
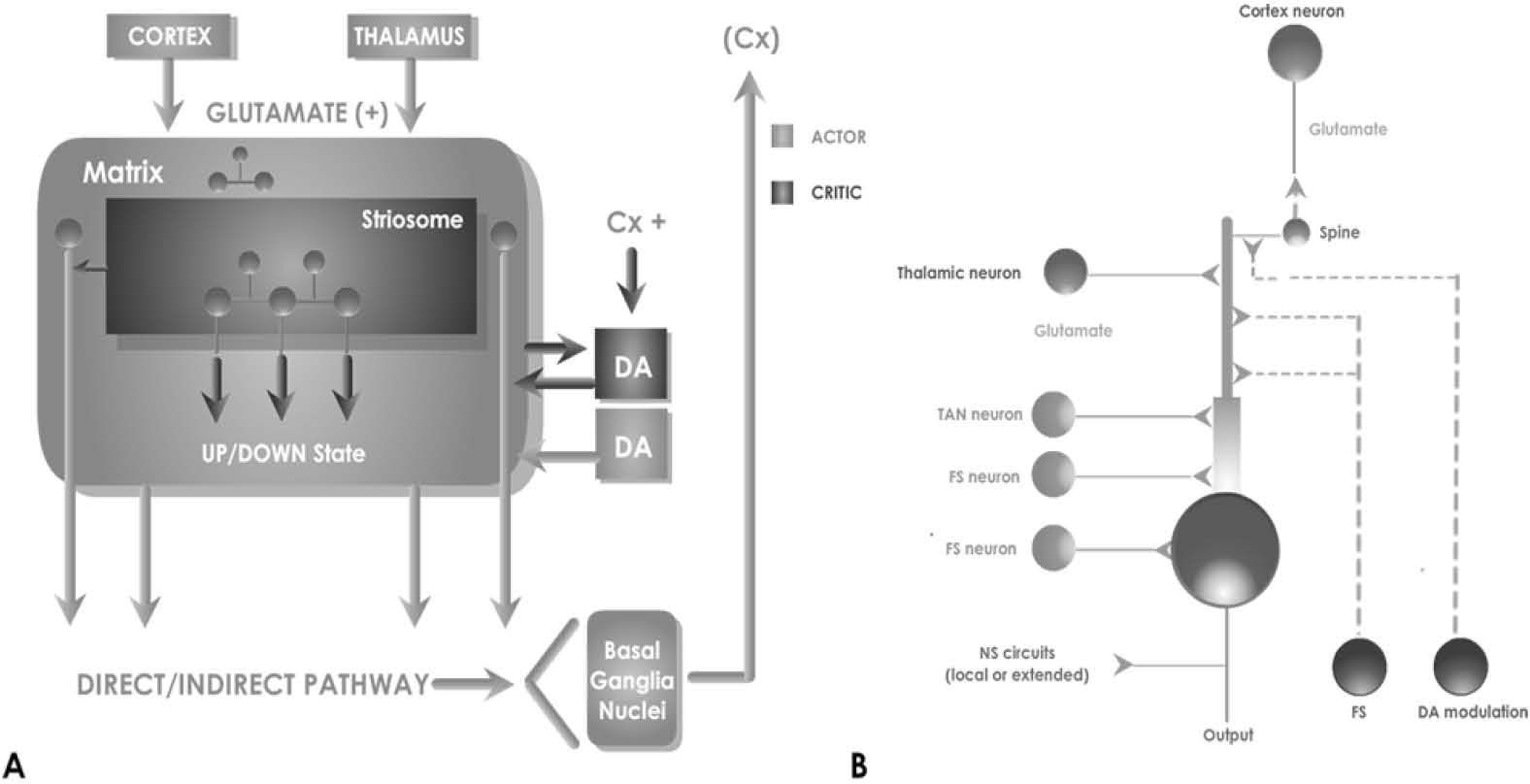
Anatomical and physiological studies have shown NS cellular architecture which reveals an internal network directed to the output of its main neuronal type: the medium spiny neuron (MSN) -an inhibitory type cell which forms a series of loops divided in two main classical circuits- calling direct and indirect pathways [59, 60] (Fig 1a).
A, classical Model of NS Connectivity. This nucleus receives excitatory input mainly from both the cortex and the thalamus regions. Its architecture is composed of patches and matrices which under modulatory influence of DA, determine the output signaling by direct and indirect pathway to the basal ganglia nuclei. The main unit is the MSN, which generates a series of inhibitory, excitatory and modulatory connections inside the NS, as shown in B.
NS would also receive input from a nucleus that can change the internal state of the network: the DA action of “substantia nigra pars compacta”, which is not considered excitatory or inhibitory, but modulatory instead [61]. This means that a dual effect is produced over the natural output MSN neurons. Depending on several network variables this can either enforce or not –or both at the same time-, the action of cortical stimulation on the MSN.
The default function of the BG output nuclei is to exert a widespread tonic inhibitory control over target structures. This starts with the NS over influence of DA modulation, which is able to promote actions through disinhibiting their associated target structures while maintaining inhibitory control over others [62]. This prevailing model was proposed by Albin et al on 1989 [55], nevertheless, a full computational model still needs to be developed [11].
We have opted for a mathematically model simplified as the basis for validating the most relevant variables and incorporating them in more controlled manner. We have chosen to refer the electrical responses and morphology of MSN, within a minimum circuit and adding the least synaptic contacts necessary to obtain comparative results. Although there are several cellular sub types that contribute to affect and modulate the membrane potential of MSN, some of them are not yet fully characterized, or are still under further discussion.
The signaling of the cells that take part in the network within the NS is complex and particular. The MSN is a cell that is normally silent, but presents this special condition in its potential membrane that keeps its value dynamically oscillating, in some moments making it easier to be excited from a summatory input [63, 64]. In their default state, MSNs are largely silent and do not respond to low input levels. However, on receiving substantial levels of coordinated excitatory input, these cells yield a significant output whose magnitude may be subsequently affected by low-level inputs, which are ineffective when presented in isolation. This dichotomous behavior is described using the terms “down state” and “up state” respectively, for these two operation modes [50].
The remain types of interneurons that conform NS architecture have also particular properties for signaling: a) “Giant Cholinergic Aspiny Cell”, electrophisiologically called “Tonically Active Neuron”, (TAN) because it produces spontaneous bursts that affects directly the MSN [65, 66]. b) “Medium GABAergic” interneurons divided electrophisiollogicaly in two types: “Fast spiking and Plateau” (FS) and “Low Threshold” spiking named after these firing characteristics [67]. All these types of interneurons are the 3-10% of the total NS architecture, and profile its input/output function by interconnecting with MSN [68] in a network outlined in Fig 1b.
We chose to consider only afferents provided to the MSN that are better identified, such as FS neurons and TAN, and check the results in the simulations according to the biological model. First, FS [65, 66], characterized histologically as parvalbumin - immunoreactive neurons in MSN affect the proximal synapses with large amplitude IPSPs, and strong effect to block signals from the axons of projection of the MSN [67]. Secondly TAN, which are characterized as cholinergic neurons have a modulatory effect, because they are activated by cortical afferents with lower latency than MSN, which in turn are their respective targets [60].
3Methods3.1 Implementation..of..the..Neostriatum..Computati onal Cell componentsA computational neural model, yet robotic or purely theoretical, has to be composed of elements that are bio-mimetic, --that is, they are intended to directly simulate neurobiological processes with the available computational resources and knowledge [69]. They have to be engineered in such a way that they provide an interface in order to allow the model to ask questions and handle some of all available variables in a controlled and limited way. A model that seeks to simulate complete behavioral competences also results impractical, because of the task scale, or impossibly, because of the lack of necessary neurobiological data, as many experiences have shown [13, 70, 71].
The process of building a biologically realistic model of a neuron, or else a network of such neurons, is based on the compartmental concept and involves the following three steps [72]:
- a)
Build a suitably realistic passive cell model, without the variable conductance.
- b)
Add voltage and/or calcium activated conductance.
- c)
Add synaptically activated conductance, and connect them to other cells in a network and provide artificial inputs to simulate the in-vivo inputs to the neuron.
The first two steps are explained bellow; the last one will be covered in the subsequent section.
For the first step, the key feature for performing excitability in a neuron is the ability for maintaining a voltage difference from inside (Vinside) to outside (Voutside). This is accomplished by the equilibrium potential Ei between ion concentrations divided by [C] given by the Nernst Equation (for the complete mathematical modeling process see the appendix in supplementary material):
In presence of several different ions in the cell, the equilibrium potential depends on the sum of their relative permeability. The eq (1) was integrated in the classical Goldman-Hodgkin-Katz solution [73-77]:
For using this theoretical approach for computing facilities, and solving it in a real time model, we need derivation of it in a linearized version:
With this, and based on experimental data, we obtain a form to predict the value of a membrane potential at a given time. Next, it needs to be implemented on an algorithm that represents a morphological model of the specific cell. We can represent a piece of a neuron as a simple RC circuit, which can be constructed in a connectionist point of view, and can be as complex as the computing facilities allow. Given the known capacitance of a piece of membrane, and starting with an initial voltage V(0), which can be obtained from another compartment serialized, or from an external input, like synapses or another stimuli, we have:
For giving a numerical solution of this passive model, it is much easier to simulate a neural activity by these compartments, where some particularities can be added like ionic membrane behavior, and morphological properties, thus allowing to differentiate neurons within a network [78]. The General Neural Simulator available for working with this technique solves differential equations with different integration techniques. Therefore, for a single compartment under a single ionic stimulation we have the following model:
Where A is the area of the membrane compartment and CM is specific Membrane Capacitance in terms of the area of the membrane, F/cm2. The actual membrane resistance (Rm) can be expressed in terms of area, as Rm = Rm/(4π r2). Thus, allowing to calculate a time constant (t) of the model as Tm=RmCm =AxCMA. We can calculate for a membrane patch:
and, using Tm as
Because of magnitudes (millivolts, milliseconds, and picoamps) and for being consistent to the International Unit System we can solve this equation as follows:
For complete mathematical deploying, see proper section in supplementary material. **
For physiological consistency, we use the inversion of resistance for calculation of ionic currents; thus gM = 103/RM is the membrane conductance in µS/cm2.
Finally for calculating the dissipation of the Voltage (V) between compartments, modeled as a continuous piece of membrane coupled with an axial resistance Ra, given the know morphological properties of the neuron, we use the Rall’s cable equation [79, 80].
This equation can be solved for several boundary conditions. axial resistance (Ra) depends on the cable geometry, diameter, length and if it is a sealed end or finite o semi-infinite cable [64, 81]. With these methodologies we have been coding, arise the three main types of neurons for this particular network: MSN, FS, and TAN. All of them were built using simplified morphological models, well tested and known as “Equivalent Cylinder models” [82, 83].
In the second step, we need to add the dynamic conductance of the ions gated in the cell, as needed for the three types of neurons used in this model. These represent the channels that drive the neuron electrical behavior. For the passive compartment explained above, the value of conductance -as inverse of resistance-, was obtained using a probabilistic function of ion diffusion interpreted as transitions between permissive or not permissive states of the molecular gates that the channels ions can cross trough; hence changing dynamically the conductance of each patch of membrane:
Where αi and βi are voltage-dependent rate constants describing the non permissive to permissive and permissive to non-permissive transition rates, respectively [84, 85]. For each of the three cells we modeled Na+, Ca+ dependent, and K+ ions are well known related variables and documented by their participation on shaping their output frequencies and wave morphology. All those responses where tested separately against the results published on the real neurons.
3.2Integration of Neural models in a NS networkIn the third Step mentioned in the above section, the model was interconnected using a simplified diagram according to Wilson, 1980 [68], and shown on Fig 1b. This schematic connectivity gives relevance to the position within the dendritic tree regarding the other connections, the back propagation between MSN, the relation between patches and matrixes, and the type of synapses within the NS: excitatory or inhibitory, plus modulatory DA effects. Following the consideration that the model is focused in the responses of MSN projections as a result of the simulation of PSP selected neuronal types, and under the modulatory effect of dopamine. This simulation is generic and can be changed in the future with the characteristics of the direct or indirect pathway, and the responses obtained can be validated and discussed.
Finally, this network was tuned with the synaptic weights needed for reproducing the operation conditions. The physiologically experimental data available have not considered data analysis processed in real time, but only qualitative analysis of outputs, thus the network model has to be tuned up empirically in cycles of trial and error [87-90].
For the integration of all constructed algorithms, we have used of the leaky integrator neuronal type as our framework [86, 87]. In principle, this proposal does not completely fit into the scope of our model, because of the idea of a dynamic membrane potential obviating the need to model an abundance of ionic channels [88]. Nevertheless, we have been updated these simplified neuronal units with full conductance-modeled neurons instead, with the cost of a high computing-resource need, but with the benefit of having a more reliable interface to compare against biological experiments. The framework then is defined by the rate of an activation change, which may be interpreted as the threshold membrane potential near the axon hillock. Let u be the total post-synaptic potential generated by the afferent input, k a rate constant which depends on the cell membrane capacitance and resistance, and a¯ the equilibrium activation, then:
Where a ≡ da/dt. The output y of the neuron, corresponding to the mean firing rate is a monotonic increasing function of a. It will be bounded below by 0 and above by some maximum value ymax which may be normalized to 1. We have adopted a piecewise linear output function of the form [89]:
The choice of this form for y is motivated by the fact that the equilibrium behavior of the model is then analytically tractable. The activation space of the model is divided into a set of disjoint regions whose individual behavior is linear, and which may be exactly determined [62, 90].
The NS model built this way admits the possibility of local recurrent inhibition. Within each recurrent net, every node is connected to one other by an inhibitory link with weight w. Let the non-zero slope in the output reaction be m, the equilibrium output of the ith node x, and the output threshold ε, then the network equilibrium state is defined by the following set of coupled equations
Now with Jk = maxi (Ji). If w.m ≥ 1, then one integral solution to (12) and (13) is:
Where δiK is the Kronecker delta. This solution may be easily verified by direct substitution.
In order to make contact with the idea of channel salience ci as input, we put Ji = wsci, where ws, is a measure of the overall synaptic efficiency of the MSN, in integrating its inputs. NS is supposed to consist of many recurrent nets of the type defined by eq. (12). Each one processing several channels; the solution in eq. (14) implies however that only those saliences, which are maximal within each network, are contenders for further processing. Now, suppose there are N NS sub-networks (as in patches or matrixes) and let cri be the salience on the ith channel of network r. Let crc(r) = maxi (cri) and P = {crk(r): r=1, ..., N}; therefore, the set of potentially active channels. Now the next step is re-label each member of P with its network index so that each local recurrent network r obeys, at equilibrium a relation of the form expressed in (14) for its maximally salient channel:
DA Modulation. For activating the action of dopamine modulation on MSN, it would be desirable to model the resulting innervation from substantia nigra compacta, and particularly the short-latency DA signals associated with the onset of biologically significant stimuli [19, 28, 91]. The whole operation of BG resides on the basis that these structures operate to release inhibition from desired actions while maintaining or increasing inhibition on undesired actions, somehow affected by the modulation of DA [92-94].
DA synapses occur primarily on the shafts of spines of MSN computationally speaking, this is suggestive of a multiplicative rather than additive process. This can be done by introducing such a multiplicative factor in the synaptic strength ws; assuming by documentation, the excitatory effects in the direct pathway and in inhibitory effects in the indirect pathway. Thus, for direct pathway, the afferent synaptic strength ws is modified to ws (1− λe), where λe means the degree of tonic DA modulation, and obeys 0≤ λe≤ 1. The function in (15) now becomes H [ci− ε/ws(1−λe)]). The equilibrium output xe−i in the ith channel of the indirect pathway is now:
In order to ease notation, we write the up state as Hi ↑ (λe). Similarly in the direct pathway:
Finally, all these sets of equations coupling compartments with all variables (currents, synapses, modulation) were solved by replacing the respective differential equation trough a difference equation that is solved at discrete time intervals [95]. This has been done through a computer neural simulator system over a high demand computer environment. The single neuron simulations have been built in “NEURON” simulator [96], and then migrated and incorporated into a Network running in a “GENESIS” simulator [41, 97]. The latter was preferred because it used implicit methods of numerical integration for accuracy besides its faster numerical capabilities for integration by these methods [72, 78].
4Results and discussionThe running simulation output was processed in real time for graphical visualization of the network activity. The data was passed through a Cartesian plane, representing the position of MSN neurons as triangles and squares. Then a MSN patch represented by the squares were stimulated and scale colored as their membrane potential changed. Some random MSN potential plots where added (four in the video shown in suppmentary material, representing arbitrarily named cell 1, 1 55, 161, 368. International System Units). The cortical stimulus simulated was defined as a 50 “spot flash” applied 20 milliseconds to only the fifth part of the active patch.
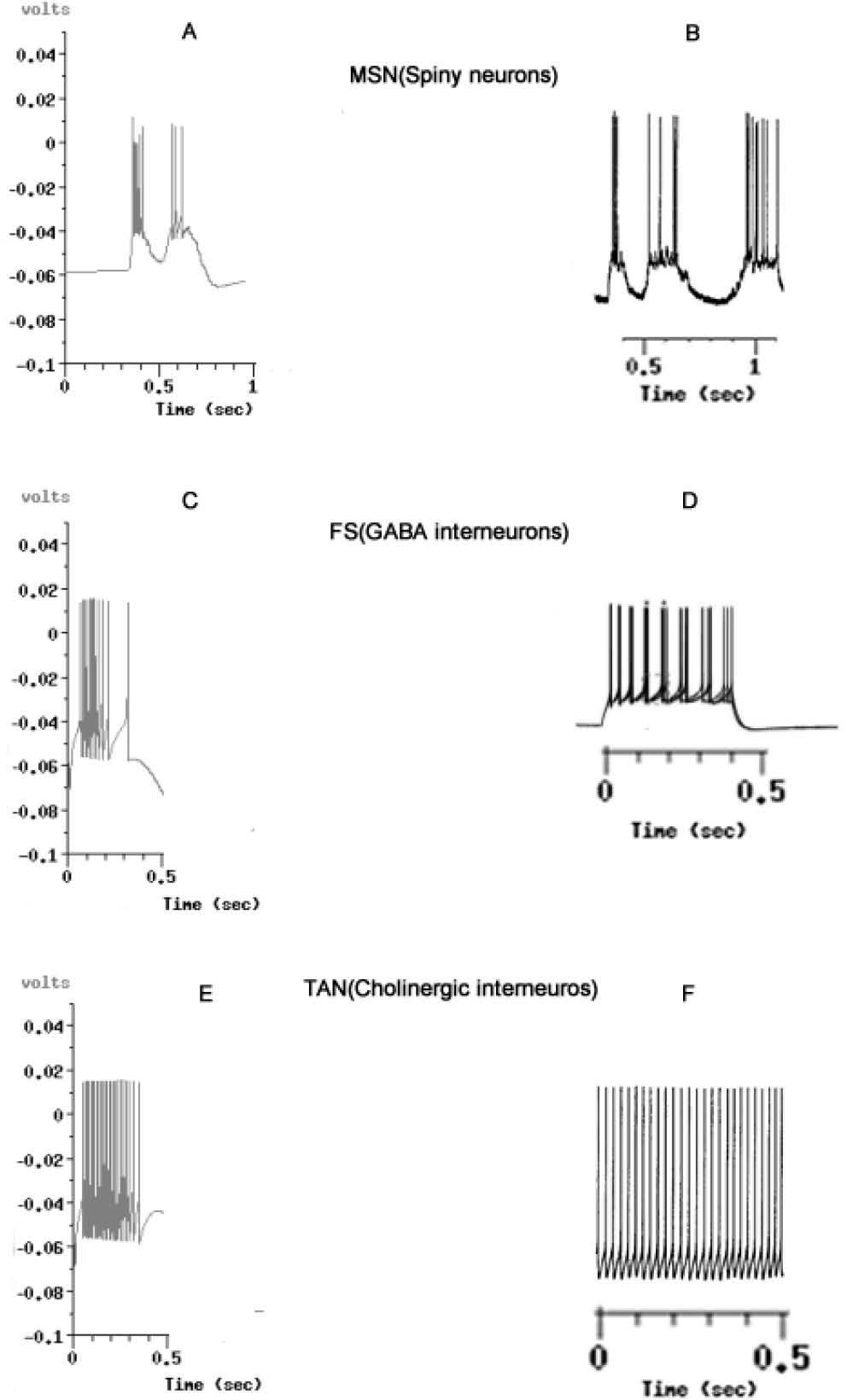
For demonstrating the validity of our model, we analyzed our outputs in two phases: in phase 1 we compared the cell units modeled against the most accepted results in biological research [47, 98-100]. The morphology and activity of those are based in the circuit, shown in Fig 2. The effect and parameters simulated in the circuit are shown in table 1. The effect of the PLTS, not entirely characterized yet as an homogeneous population of cells, has been reported to actively participate in the regulation of the balance between excitation and inhibition in cortical circuits to the NS, Beierlein et al. [122], Silberberg and Markram [123] and Kapfer et al. [124] but only evoke a sparse and relatively weak GABAergic IPSCs in MSN [67]. So, we do not have conclusive results on its direct effect on GABAergic MSN. Although is theorized about whether its main function focuses on the modulation of SOM / NPY NOS [68, 69, 70]. Because of that, for purposes of this model are not considered.
Voltage output graphics simulated against biological models, taken from known and accepted reports. A: Simulated output from MSN. B, MSN from experiments performed by Wilson & Kawaguchi in 1996 [50]. C. Simulated output from FS GABAergic interneurons. D. FS from experiments by Tepper in 2010 [101]. E, Simulated Output from TAN, Cholinergic Inter-neurons. F. Results reported by Bennet et al. in 2010 [102]. In all simulations, ionic environment could be reproduced in the network for the equivalent of 0.5 milliseconds of the biological activity. The graphics B,D and F are not comparatively scaled. With A,C and E.
Cell properties used in simulated NS circuitry.
| Cell Type | Input Resistance MΩ | Time constant (ms) | Effect on MSN | Dopaminergic effect simulated |
|---|---|---|---|---|
| MSN | 20-60 | 5-15 | -- | Only considered Depolarization |
| FS | 50-150 | 7-9 | Proximal synapses. Can delay or block completely spiking on PSP | Depolarization and increase of Input resistance |
| TAN | 71-105 | 17.8-28 | Moderate effect, as modulator of excitability of MSN sensorial activation from cortex (Misgeld 1986) | none |
The main insights of the waves’ morphology of MSN, FS [101] and TAN [102] indicate that neurons could be visualized in the Time/Voltage plots, although some conductance need to be adjusted from the experimental findings to fit the curves obtained from the electrophysiological sets where real neurons are recorded.
The anomalous rectification classically reported in MSN need to be verified in function of the currents modeled [47]. Classically up to six different conductance have been described in MSN [50, 103-105], but data about their respective weights against each other and proper location in the cell compartments, are neither available nor complete [106].
In the state-of-art regarding experimental procedures which have been done with MSN in vitro and in vivo, methodologies that require isolating or blocking each current have been used [107, 108]. Thus, complete model would need the simulation of these six conductances mainly characterized, plus the network parameters selected, which represent a series of variables that are difficult and impractical to analyze as a whole. We have chosen to simplify the model representing the activity of each cell with a leaky integrator function, the procedure for this is explained in supplementary material**. The model used only one projection cell for analysis, leaving the other inactivated for further study. There are different procedures available where some steady values vary such as input resistances or, where time constants are mostly altered by either micro-pipettes, or the type of recording device [109].
Most of the experiments have been carried in different species [110, 28, 54, 85, 86], and tough there is some acceptance on the fact that are equivalent, there is still a lot of variables that must be taken into account for a mathematical model that goes from simple to complex structures, and can deliver a whole output of all these isolated conductances in real time [111-113].
Considering all this background and though the simulated neurons act real enough to be compared to real ones, it is still under consideration whether the encountered differences are due to a variable not considered or to a current or neural integration just not discovered yet. In electrophysiology, reports are still discussed to determine whether the conductances actually characterized are solid enough by themselves or there are still other different interactions to be discovered [114]. The whole picture can be taken with a model that integrates the knowledge really available, that would encourage further use and perfecting of this model. Similarly as MSN’s, in the case of FS and TAN neurons the results were still accurate enough but with more differences derived from the very novel biological data available regarding their function [101, 102, 115].
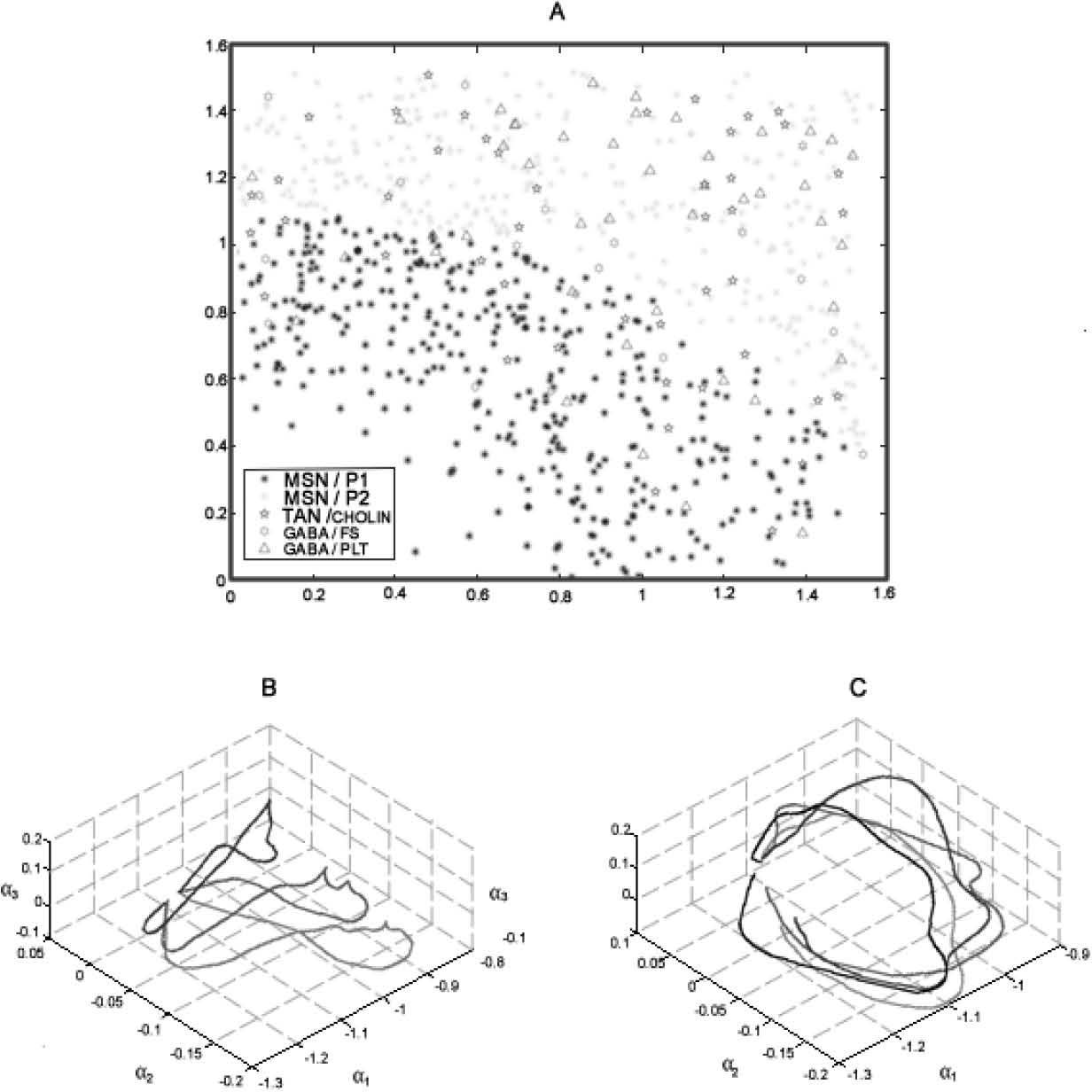
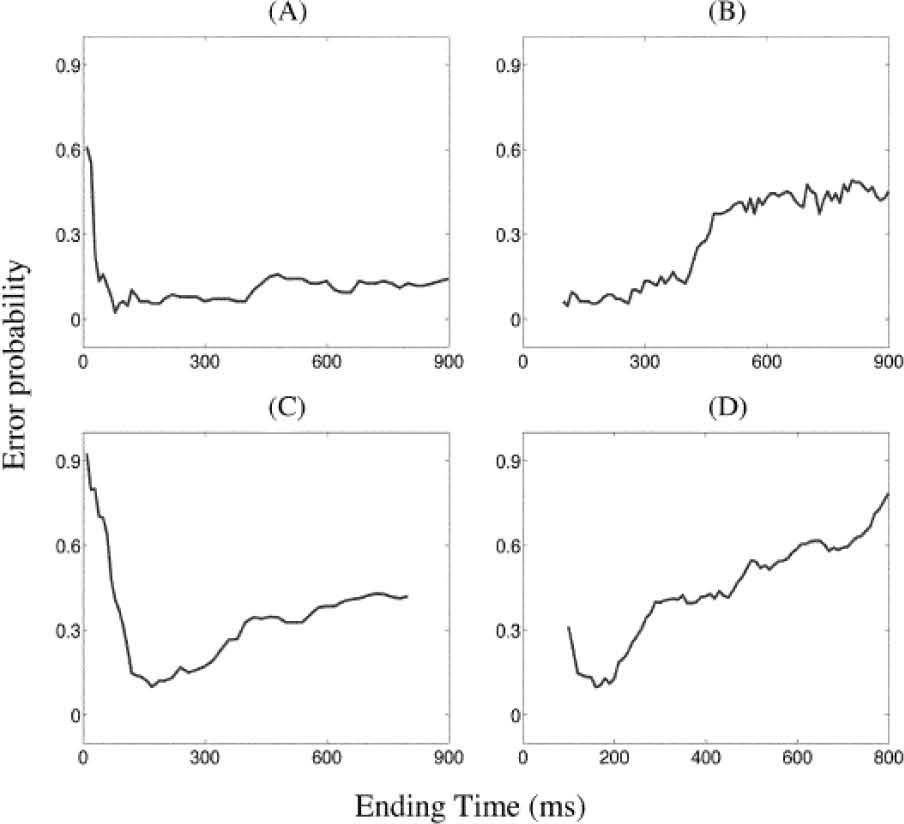
In phase 2 we analyzed the model’s behavior as a whole network (fig 3a). A video reconstruction of this is available in supplementary material** The main issue at this stage is testing against the biological specimen, because there are no experiments available to compare. Nonetheless, we do have information about field responses and postsynaptic responses, which indirectly have been useful for inferring the activity of the NS. Notwithstanding the lack of biological data to compare against, cortical and sub-cortical waves have been analyzed in many computational models as a Bayesian problem [13, 116], using two-step Karhunen_loeve (KL) decomposition. Briefly, each time-step was split up into a sequence of 10 ms overlapped encoding windows. Within each window, the movie was projected as a point using double KL decomposition in a suitable low dimensional B-space (fig 3b). The sequence of point in the B-space rise a strand, called a β-strand. Each NS wave was represented as a vector-valued time series given by the β-strand, and the detection task operated by DA was to discriminate strands from different combination of modulation status, empirically tuned as explained above. That is how the problem was reduced to a Bayesian Problem. Expanding detection windows (EDW) a sliding detection windows (SDW) where applied over the β-strand. The combination of encoding and decoding windows made it possible to localize the NS target in space as a function related to double-input-time-delay stimuli. This means that this analysis enables to show, in a rather simplified way, activation/no activation of NS network patterns against activation/no activation of DA Modulation (fig 4), demonstrating with it that modulation of DA over the tree neuron network configured in the framework is possible.
A, Representation of the Simulated Neural Units over a Cartesian plane. The main neuron MSN is segregated in a patch (MSN/P1) and matrix (MSN/P2) region, representing 97% of the whole population.TAN and FS interneurons, representing 5% of the network, are incorporated and connected using a pattern described in the text. In the bottom: Phase trajectories in A-space, product of double KL decomposition. This represents the responses of three different stimuli on the network, and over two different conditions: B without the influence of DA Neuromodulation (top), C, with the influence of DA Neuromodulation. The first decomposition represents a wave as a linear combination of a series of spatial modes with time-varying coefficients.Thus, the wave is adequately represented (as has already been shown by Senseman and Robbins [10]) by a trajectory in a phase space called A-space. Most of the energy contained in the original wave can be captured by the decomposition coefficients corresponding to the first three principal modes. A further reduction of the dimensionality of the wave is achieved by a second KL decomposition which maps the trajectory in A-space into a point in a low-dimension space. A-space is spanned by temporal modes. The data was processed by using windowing techniques, including a sliding encoding window in the wave encoding process and expanding detection window (EDW) and sliding detection window (SDW) techniques in the information decoding process, to estimate the position of stimuli in space (see supplementary material for visualization**).
Detection of error probability (activation rate) as a function of the ending of time windows. A. Detecting the stimuli by EDW approach. B. By using SDW approach. C. With DA modulation, by EDW approach. D. With DA modulation by SDW approach. This analysis shows the overall action of DA modulation over the probabilistic activation of the NS simulated network.
The leaky integrator function that is present here is a classical framework that uses simplified neuronal units that are just represented as circuits without considering the operation electric properties of ionic conductances within the cell [117]. It has been used for building proposals of data processing in neural structures [78, 111], but all those mathematical constructs cannot be contrasted against the biological models for feedback because their own information nature and mathematical building are not the same, especially from the point of view where the neural tissue processes information in an analogical manner [83, 90, 118, 119]. For this reason, there are different proposals and alternatives against leaky integrator function elsewhere, specially using the fuzzy integrator technique [7, 120, 121].
The modeling work considered above, can be applied to demonstrate signal selection by the BG, and the proper response of the cells that are mathematically simulated and embedded on it, rather than theoretically apply action selection per se. So that we can convincingly show that the basal ganglia model is able to operate as an effective action selection device, we believe it needs to be embedded in a real time sensory motor interaction with the physical world, or else through a given construct that simulates so.
The author thank Posgrado en Ciencias Biologicas of National University of Mexico for the received formation during his postgraduate studies. This work was supported by PAPCA–Iztacala UNAM-2014-2015, and PAPIIT-DGAPA UNAM IN215114 grants.






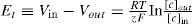
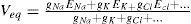
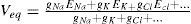
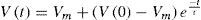
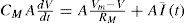
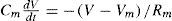
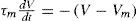

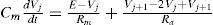

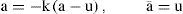
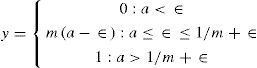
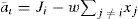
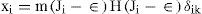
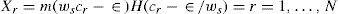
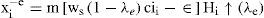
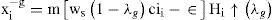
![Voltage output graphics simulated against biological models, taken from known and accepted reports. A: Simulated output from MSN. B, MSN from experiments performed by Wilson & Kawaguchi in 1996 [50]. C. Simulated output from FS GABAergic interneurons. D. FS from experiments by Tepper in 2010 [101]. E, Simulated Output from TAN, Cholinergic Inter-neurons. F. Results reported by Bennet et al. in 2010 [102]. In all simulations, ionic environment could be reproduced in the network for the equivalent of 0.5 milliseconds of the biological activity. The graphics B,D and F are not comparatively scaled. With A,C and E. Voltage output graphics simulated against biological models, taken from known and accepted reports. A: Simulated output from MSN. B, MSN from experiments performed by Wilson & Kawaguchi in 1996 [50]. C. Simulated output from FS GABAergic interneurons. D. FS from experiments by Tepper in 2010 [101]. E, Simulated Output from TAN, Cholinergic Inter-neurons. F. Results reported by Bennet et al. in 2010 [102]. In all simulations, ionic environment could be reproduced in the network for the equivalent of 0.5 milliseconds of the biological activity. The graphics B,D and F are not comparatively scaled. With A,C and E.](https://static.elsevier.es/multimedia/16656423/0000001200000003/v2_201505081651/S1665642314716360/v2_201505081651/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![A, Representation of the Simulated Neural Units over a Cartesian plane. The main neuron MSN is segregated in a patch (MSN/P1) and matrix (MSN/P2) region, representing 97% of the whole population.TAN and FS interneurons, representing 5% of the network, are incorporated and connected using a pattern described in the text. In the bottom: Phase trajectories in A-space, product of double KL decomposition. This represents the responses of three different stimuli on the network, and over two different conditions: B without the influence of DA Neuromodulation (top), C, with the influence of DA Neuromodulation. The first decomposition represents a wave as a linear combination of a series of spatial modes with time-varying coefficients.Thus, the wave is adequately represented (as has already been shown by Senseman and Robbins [10]) by a trajectory in a phase space called A-space. Most of the energy contained in the original wave can be captured by the decomposition coefficients corresponding to the first three principal modes. A further reduction of the dimensionality of the wave is achieved by a second KL decomposition which maps the trajectory in A-space into a point in a low-dimension space. A-space is spanned by temporal modes. The data was processed by using windowing techniques, including a sliding encoding window in the wave encoding process and expanding detection window (EDW) and sliding detection window (SDW) techniques in the information decoding process, to estimate the position of stimuli in space (see supplementary material for visualization**). A, Representation of the Simulated Neural Units over a Cartesian plane. The main neuron MSN is segregated in a patch (MSN/P1) and matrix (MSN/P2) region, representing 97% of the whole population.TAN and FS interneurons, representing 5% of the network, are incorporated and connected using a pattern described in the text. In the bottom: Phase trajectories in A-space, product of double KL decomposition. This represents the responses of three different stimuli on the network, and over two different conditions: B without the influence of DA Neuromodulation (top), C, with the influence of DA Neuromodulation. The first decomposition represents a wave as a linear combination of a series of spatial modes with time-varying coefficients.Thus, the wave is adequately represented (as has already been shown by Senseman and Robbins [10]) by a trajectory in a phase space called A-space. Most of the energy contained in the original wave can be captured by the decomposition coefficients corresponding to the first three principal modes. A further reduction of the dimensionality of the wave is achieved by a second KL decomposition which maps the trajectory in A-space into a point in a low-dimension space. A-space is spanned by temporal modes. The data was processed by using windowing techniques, including a sliding encoding window in the wave encoding process and expanding detection window (EDW) and sliding detection window (SDW) techniques in the information decoding process, to estimate the position of stimuli in space (see supplementary material for visualization**).](https://static.elsevier.es/multimedia/16656423/0000001200000003/v2_201505081651/S1665642314716360/v2_201505081651/en/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
