In the context of China's knowledge economy, cluster-based technological innovation can promote the communication of knowledge among industries, advancing the industrial structure. This study constructs the Ricardian model with the differences in productivity between different sectors to explore the mechanism of connected knowledge spillovers of technological cluster innovation driving efficient industrial structure, applying a spatial Durbin model to Chinese provincial panel data from 2003 to 2017 to analyze spatial effects. The results demonstrate a significant positive correlation between regional efficient industrial structure and technological cluster innovation under connected knowledge spillovers. These effects increase sequentially from the perspectives of the technology introduction, technology upgrade and independent innovation. Moreover, technological cluster innovation exhibits a significant backwash effect, negatively influencing the efficient industrial structure of neighboring areas. Finally, the study discusses some policy recommendations on optimizing the regional technological innovation environment.
Driven by the accelerated adjustment of the global industrial structure and unprecedented development of economic globalization, the global economy has entered a path of rapid growth. The status of industrial structure upgrade and optimization continues to rise and is increasingly becoming the driving force of a new era of global economic development. The innovation-driven is the foundation of economic transformation and upgrade, development of industries toward high- and mid-grade positions in the global value chain, and the sustainable development of economic society. With the accelerated process of global informatization and networking, severe challenges are hindering economic development in China and new modes of development are urgently needed (He et al., 2021). Technological cluster innovation has an important influence on the transformation of economic growth and sustainable economic development (Kihombo et al., 2021). In the context of China's knowledge economy, technological cluster innovation can effectively organize and apply existing knowledge to promote knowledge spillovers among industries to achieve efficient industrial structure. This study focuses on analyzing the spatial effect of technological cluster innovation to promote efficient industrial structure from the perspective of dynamic changes, and mainly verifies the existence of the spatial effect by constructing spatial Durbin model under connected knowledge spillovers.
The relationship between knowledge spillovers and the sustainable development of regional economies is demonstrated, presenting a new theory of economic growth that emphasizes the profound effect of knowledge spillovers (Huber, 2012). There is currently no unified scholarly consensus regarding the definition or the nature of the effect of knowledge spillovers. Marshall (1920) was one of the pioneers in studying the external characteristics of knowledge acquisition. Arrow (1962) used the effect of knowledge spillovers on economic growth to measure the externality of knowledge. Knowledge externalities were divided into “Marshall–Arrow–Romer (MAR) externalities” within the same industry and “Jacobs’ externalities” between different industries by Glaeser et al. (1992). Multiplexity and heteromorphism in knowledge exchanges are confirmed by Giusti et al. (2020). According to the direction of knowledge spillover, scholars divide it into horizontal and vertical knowledge spillover (Le & Pomfret, 2011; Rojec & Knell, 2018). Under the economic branch of new economic geography and endogenous growth theory, knowledge spillover is an important variable in explaining regional economies, technological innovation, and industrial agglomeration (Altunbaş et al., 2013; Serrano-Domingo & Cabrer-Borrás, 2017). Technological innovation has the characteristics of giving real events the novelty of conception and successful realization. The complexity of development process of the technological innovation makes it difficult to define it at home and abroad, but many literatures revealed the internal mechanism of technological innovation in detail (Choi et al., 2016). More scholars explained the development trajectory of technological innovation from the aspects of technological innovation capability, technological innovation efficiency, its influencing factors (Adamides & Karacapilidis, 2020; Cruz-Cázares et al., 2013; Talukder, 2012) and its measure indicators (Taques et al., 2021). Moretti & Biancardi (2020) focused on the effect of open innovation on firm performance. Previous research on technological innovation and industrial structure optimization and upgrade primarily focused on aspects such as the internal mechanism of technological innovation (Zhou & Li, 2012), the effect of technological innovation (Karltorp et al., 2017), the factors influencing the optimization and upgrade of industrial structure (Li & Lin, 2017), and the relationship between industrial structure transformation and economic growth (Dong et al., 2020). Romer (1986) and Lucas (1988) endogenized technological progress in the theory of endogenous economic growth, thus proposing that technological progress could promote the adjustment of industrial structure. From an empirical point of view, Wu & Liu (2021) found that technological innovation has a positive effect on the local industrial structure upgrade, but its indirect effect is not significant.
Although existing research has investigated knowledge spillovers and technological innovation as drivers of industrial structure upgrade, the issues above remain understudied. To address this deficiency, this study aims to analyze the following questions: how does technological cluster innovation affect efficient industrial structure from the perspective of connected knowledge spillovers? Does technological cluster innovation have a positive or negative spatial spillover effect on efficient industrial structure of neighboring areas? What are the differences in the impact of technological cluster innovation driving efficient industrial structure from the perspective of different types of connected knowledge spillovers? Based on the questions above and previous research approaches, this study uses Chinese provincial data from 2003 to 2017 to analyze the spatial effect of technological cluster innovation driving the efficient industrial structure through connected knowledge spillovers.
The contributions of this study are threefold. First, the internal mechanism of technological cluster innovation is investigated from a new perspective, focusing on the formation of a complex interactive mode of technological innovation, wherein the innovation chain embeds and fully integrates into the industrial chain, followed by a quantitative matching approach. Second, referencing previous research, a Ricardian model with the differences in productivity between different sectors is constructed to analyze the mechanism of technological cluster innovation driving efficient industrial structure. Third, a geographical and technological distance spatial weight matrix integrating various knowledge spillover variables is constructed to measure its spatial effect on efficient industrial structure. Existing literature predominantly focuses on spatial weight matrices based on geographical distance, ignoring the effect of knowledge spillovers (Feng et al., 2021; Wu & Liu, 2021). According to the directionality characteristics of knowledge spillovers, we construct a spatial weight matrix based on both geographical and technological distance, build a spatial Durbin model, and explore the spatial effect of technological cluster innovation as a driver of efficient industrial structure.
This study is organized into six sections. Section 1 introduces the background and significance. Section 2 defines the main variables of the study. Section 3 introduces the relevant literature and proposes hypotheses. Section 4 describes the research materials and methods. Section 5 describes the data analyses and related discussion. Section 6 presents the conclusions and makes policy recommendations.
DefinitionConnected knowledge spilloversThe concept of knowledge spillover refers to a reengineering of knowledge and a method of pursuing knowledge diffusion, which measures the spillover effects when it is unconsciously leaked. In this way, enterprises obtain benefits without paying a price. Knowledge spillover has been demonstrated among domestic enterprises (Audretsch & Belitski, 2020; Paci & Usai, 2009) and domestic and foreign enterprises (Guo et al., 2021; Wang & Wu, 2016). Franco & Esteves (2020) tried to understand the cluster network, the mechanism for the share of knowledge. Altunbaş et al. (2013) discovered the differential effects of knowledge spillovers within and between industries on urban development. This study presents a novel perspective regarding the study of directional knowledge spillovers and proposes the concept of connected knowledge spillovers. As shown in Fig. 1, connected knowledge spillovers refer to the knowledge spillover multiplier effect that is generated by multiple bodies or organizations, considering both horizontal knowledge spillovers (between different industries within the same profession) and vertical knowledge spillovers (between upstream and downstream industries).
Technological cluster innovationTechnological cluster innovation is a new mode of innovation that is derived through enterprise or industry clusters. Ruoslahti (2020) explored the complexity of collaboration for innovation. Overall, technological cluster innovation is a complex and sophisticated form of cooperative innovation. It is a process in which an industrial chain is embedded in the front, middle, and back ends of the industrial chain, and industrial and innovation chains are integrated and transformed into a form of technological convergence and diffusion. Through embedding and integration, emerging industries cluster in space through complex network interaction. Regional technological cluster innovation refers to the organic unity of technological and industrial organization innovation. Assume that there is a “craft innovation (C), product innovation (P), and service innovation (S)” innovation chain within an enterprise, and an “upstream enterprise (U), midstream enterprise (M) and downstream enterprise (D)” industrial chain within an enterprise (Nonaka et al., 2000). With increasing specialization in the social division of labor, a complex technological innovation network interaction model emerges to achieve technological cluster innovation when an innovation chain is embedding and integrating with the related industry chain (Fig. 2).
Efficient industrial structureThe main goal of the optimization and upgrading of the industrial structure is to optimize the national economic benefits, improving the efficiency of the industrial structure and the level of the industrial structure through industrial adjustment. The optimization of the industrial structure has been in a state of change. At different stages, the content of the optimization and upgrading of the industrial structure is different. This is also the basic feature of the evolution law of the industrial structure, which lays the foundation for the sustained and rapid development of the national economy (Peneder, 2003). Efficient industrial structure refers to the industrial structure of a country or region with high processing and high technology. It is the existence of an industrial alliance system with significant economic benefits, coordinated industries, and intricately linked industrial structures that reflects such efficiency. With the development of efficient industrial structure, society will establish higher resource allocation efficiency.
Literature reviewExtant studies have primarily focused on several relevant considerations. The first stream of literature has focused on the impact of knowledge spillovers on technological innovation (Philipson, 2020). From the perspective of the internal logic of knowledge spillovers and technological innovation, the spatial attenuation of knowledge spillover efficiency caused by the locality of knowledge spillover will promote the innovation activity within a cluster geographically, increasing innovation output through the formation of a cluster-type innovation network development model (Anselin et al., 1997; Audretsch & Feldman, 1996). In the process of mutual exchanges and contacts between economic entities in different locations, geographical knowledge diffusion occurs unconsciously (Miguélez & Moreno, 2015). Most literature has analyzed the topic from a regional perspective. Jaffe et al. (1993) introduced the mechanism of knowledge spillover to improve regional technological innovation in the context of patent citations. From the perspective of absorptive capacity, Fu & Díez (2010) investigated its role in promoting the transformation of technology flows generated by the network and labor mobility in regional innovation. Some studies have analyzed spillover effects at the industrial or enterprise levels. Ribeiro-Navarrete et al. (2021) explored factors influenced business performance of KIBS. Ode & Ayavoo (2020) found that knowledge management practices could have positive effect on firm innovation. Enterprises’ technological innovation capabilities were also found to be affected by local knowledge spillover effects (Grillitsch & Nilsson, 2015). Qiu et al. (2017) research determined that both local and global knowledge spillovers in relatively developed regions could enhance regional technological innovation capabilities. Lin (2015) demonstrated that firms located near a knowledge center experienced higher volatility, suggesting that knowledge spillovers contribute to corporate innovation. Whether at the micro enterprise level or the macro regional level, the existence and significance of knowledge spillover is irrefutable. Regional technological innovation increases through mutual learning and information exchange between innovation subjects both within and between regions (Caniëls & Verspagen, 2001).
Another stream of research has investigated the effect of technological innovation on industrial structure upgrade. Changes in the demand structure and labor productivity generated by technological innovation are principal driving forces for regional industrial structure upgrade (Antonelli, 2014; Ngai & Pissarides, 2007; Peneder, 2003). Altenburg et al. (2008) examined China's economic development, asserting that China has improved its technological imitation and original innovation capabilities through the establishment of a national industrial innovation system and technological innovation system, thereby achieving the upgrade of its industrial structure. Wu & Liu (2021) found technological innovation to have a significant positive spatial spillover effect on industrial structure upgrade. Xia et al. (2020) focused on the technological advancements achieved through outward foreign direct investment (OFDI), which can significantly promote industrial structure upgrade. Furthermore, some scholars have explored the spatial effect of technological innovation on industrial structure upgrade, indicating that technological progress could significantly promote the industrial structure upgrade of a region; however, it has no significant impact on surrounding areas (Feng et al., 2021).
Research on the joint analysis of the relationships between knowledge spillovers, technological innovation, and industrial structure upgrades is limited. Some scholars have explored and verified the positive role of technological innovation in promoting industrial structure upgrade under the influence of knowledge spillovers from the perspectives of higher education, financial development, and digital economy (Jiang et al., 2020; Su et al., 2021; Wu & Liu, 2021). A few scholars have conducted research on the impact of spillover effects, such as Xia et al. (2020), who constructed a fixed effects model, asserting that technology spillovers brought by OFDI promote industrial structure upgrade through technical structure and technological innovation. Nevertheless, the study did not specifically distinguish the differential effects based on the directions of knowledge spillovers.
In summary, previous literature has largely focused on the mechanism and empirical data between two factors in knowledge spillovers, namely, technological innovation and industrial structure upgrade, and studies investigating the three factors are relatively scarce. Some scholars have attempted to analyze them by proposing theoretical frameworks and fixed effects models, providing policy recommendations for promoting industrial structure upgrade through technological innovation (Xia et al., 2020). However, these studies are insufficient in three ways. First, existing literature lacks the definition of connected knowledge spillovers and technological cluster innovation and fails to acknowledge innovation chain embedding and integration within industry chains. This perspective is helpful for interpreting the driving effect of technological cluster innovation on efficient industrial structure. Second, the application of mechanism model is lacked. Most research analyzes these constructs using a theoretical framework, and mechanism model analysis of technological innovation on industrial structure upgrade is limited. Third, previous empirical research is insufficient for capturing spatial pertinent relationships. Studies have predominantly explored these relationships based on the mediation effect and fixed effects models; therefore, there is a lack of analysis applying spatial effect models. Subsequently, this study constructs a spatial weight matrix of connected knowledge spillovers to examine the direction of knowledge spillovers from the perspective of both geographical and technological distance, which will improve, supplement, and expand upon existing research.
Based on previous research status and real-world circumstances, this study proposes the following hypotheses:
Hypothesis 1 (H1): There is a significant positive relationship between technological cluster innovation and efficient industrial structure with connected knowledge spillovers.
Hypothesis 2 (H2): From the perspective of connected knowledge spillovers, technological cluster innovation inhibits the efficient industrial structure in neighboring areas.
Materials and methodsTheoretical modelIn the context of connected knowledge spillovers, technological cluster innovation promotes the cooperation of regional innovation bodies through full agglomeration of technological factors, such as capital, high-tech talents, and institutional factors in the region. It drives enterprises or industries developing towards becoming technology-intensive, high-tech, and high-productivity, and the efficiency of industrial structure will be improved through internal promotion and pulling effect.
Ricardo's (1817) theory of comparative advantage is an extension and revision of Adam Smith's theory of international trade division. This theory proposes the principle of relative advantage in international trade, laying a foundation for the theoretical development of international trade and division of labor. With the extension of commodity transportation distance and the development and update of various trade policy measures, the assumption of perfect competition in the standard Ricardian model has been objectively broken down. Scholars have incorporated the hypothesis of imperfect competition into the model to enhance the model's ability to anticipate trade flows. According to the proportional relationship between global demand and the production capacity of countries with comparative advantages in supplying products, Dornbusch et al. (1977) studied the conditions of complete and partial divisions of labor. Costinot (2009) considered the differences in productivity between different countries and industries and analyzed the impact of the tradeoff between the benefits of specialization and transaction costs on countries’ degree of labor division across sectors. The above expansion model from Costinot carefully considers different enterprises or industries with different levels of productivity. This perspective is very suitable for this study, as the approach is based on regional differences in technological cluster innovation capabilities that lead to variations in the production efficiency of various enterprises or industries.
This study combines the research of Dornbusch et al. (1977) and Costinot (2009), constructing a Ricardian model with the differences in productivity between different sectors to explore the mechanism of technological cluster innovation as a driver of efficient industrial structure. In the technological cluster innovation network, factors such as technology, knowledge, high-tech talent, and institutional factors will be fully agglomerated under the comprehensive effects of technique acquisition, technological transformation and upgrade, and independent innovation. The agglomeration will ultimately promote efficient industrial structure. There are differences in production efficiency between enterprises or industries due to differences in regional capabilities in technological cluster innovation, which generates production factor flows to high-tech industries with great production efficiency. The number of high-tech industries and the proportion of value added for industrial enterprises are continuously rising, which achieves efficient industrial structure.
Suppose that each enterprise produces only one product, which includes a total of a tasks. We can obtain the following:
where and e−1θis the level of technological cluster innovation, the salary of each employee in the enterprise is M, and the number of fixed teams in the enterprise is R; thus, the number of work tasks for each employee is a/R. Before production, each employee needs to be trained. The learning cost that each employee must pay is also a/R. Therefore, the labor consumed by each task in production is given as follows:It is also assumed that the number of workers employed by the enterprise for production is g, then the expected output can be shown as follows:
thus, the profit function of the enterprise can be written as follows:where the price of the product is p and wage is w. To find the first-order derivative of R in the above formula, the optimal division of labor of an enterprise isR=a+a2+4·a·M2M, and the demand for labor per unit product can be derived asx=[(Ma−1R)·e−Rθ]−1.Based on the Ricardian model, the ratio of labor demand per unit product in Region 1 and Region 2 can be expressed as follows:
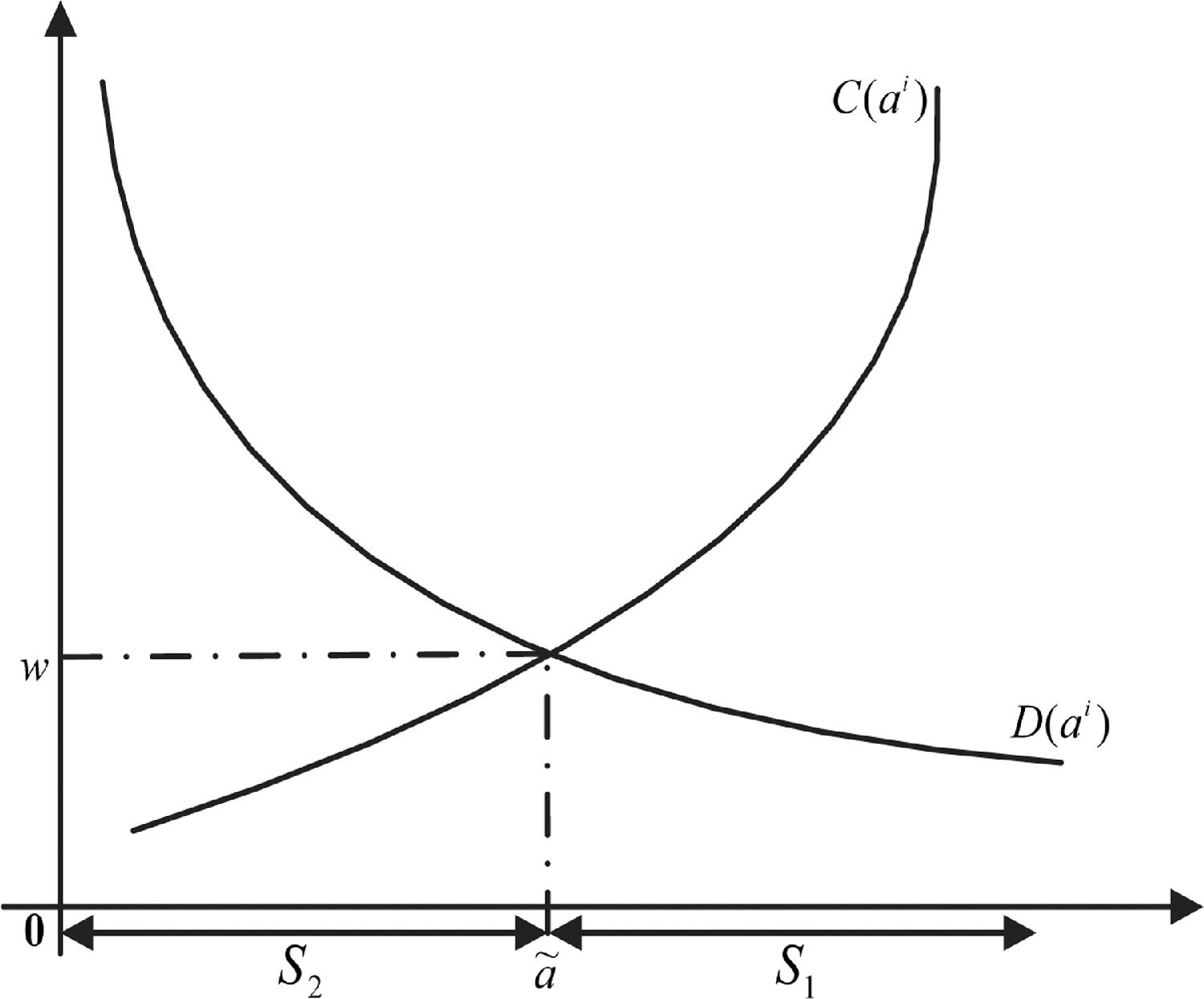
When two regions have the same level of human capital and products, the higher the level of technological cluster innovation is, the greater is the value of B. If θ1>θ2, Region 1 has a comparative advantage in producing high-complexity products. The market gradually approaches equilibrium under the adjustment of invisible forces. When the market is in equilibrium, region c requires the following:Furthermore, according to the Walrasian theory of general equilibrium, we know that the labor market in Region 2 exists as follows:
where a~ exists, while w=C(a~) and w>C(a~) if and only if aiLet C(a~)=D(a~); therefore, there is a~=f(θ), that is faptaradummyentityaptaradummyx27;(θ)>0. Free trade between regions determines the stability of the relative wages; therefore, an increase of θ1 leads to a right shift of D(ai) and the scope of S2 is expanded. The destination of product production will shift accordingly. Region 1 concentrates on producing technology-intensive high-tech products and developing high-tech industries. This further indicates that a high level of technological cluster innovation will drive efficient industrial structure (as shown in Fig. 3).
Establishment of spatial weight matrixHorizontal and vertical knowledge spillovers will occur within an industry, among industries, and among upstream and downstream industries, wherein connected knowledge spillovers will also appear in the form of a network. Spillovers are realized through technical knowledge sharing among regional enterprises or industries; therefore, a geographical and technological distance spatial weight matrix is constructed combining geographical distance measures and knowledge spillover measures (Aiello & Cardamone, 2008). The spatial weight matrix can be expressed as follows:
where H¯i=1/(ti−1−ti+2)∑ti−1tiHit,H=1/(ti−1−ti+1)∑i=1n∑ti−1tiHit,S¯i=1/(ti−1−ti+2)∑ti−1tiSit,S=1/(ti−1−ti+1)∑i=1n∑ti−1tiSit,I¯i=1/(ti−1−ti+2)∑ti−1tiRDitIOit,I=1/(ti−1−ti+1)∑i=1n∑ti−1tiRDitIOit,R¯i=1/(ti−1−ti+2)∑ti−1tiISitIOit,R=1/(ti−1−ti+1)∑i=1n∑ti−1tiISitIOit,Z¯i=1/(ti−1−ti+2)∑ti−1tiZit,Z=1/(ti−1−ti+1)∑i=1n∑ti−1tiZitis geographical distance matrix.1WLDI,WLDRandWLDZ are the spatial weight matrices for connected technology introduction, connected technology upgrade, and independent innovation, respectively. H¯i refers to the stock of human capital in the province, expressed in terms of the per capita years of education.2H represents the total stock of human capital. S¯i represents the total assets of the three kinds of investment enterprises in provincial region i. S refers to the sum of the total assets of the three kinds of investment enterprises.I¯irepresents total R&D activities in provincial region i, expressed in foreign funds of internal expenditures of R&D expenditures. Imeasures the total R&D activities.R¯iis the total R&D activities in provincial region i, expressed in the weighted sum of contract technology fees of foreign technology import and technological transformation, digestion, and absorption of industrial enterprises above designated size. R measures the total R&D activities.IO is the total industrial output value.Z¯i is the independent innovation capability in provincial region i, expressed in terms of the weighted value of the added value of high-tech industry, total high-tech industry import and export, number of authorized patent applications, number of scientific and technological papers, and value of contract turnover in the technology market.3Variable descriptionTechnological cluster innovation (JI)Technological cluster innovation refers to a coordinated process of technology innovation in which technology is clustered between industries. Such cooperation improves industrial production efficiency in a win–win situation. In this study, technological innovation efficiency is used to represent technological cluster innovation (JI) and measure it through input–output indicators. The input indicators represent the market benefits of new technologies, expressed in the new product output value and new product sales revenue of the high-tech industry. The output indicators are measured from the perspective of technological innovation achievements, expressed in the number of new product development projects and patent applications of high-tech industry (Cruz-Cázares et al., 2013). In this study, we use the provincial industrial producer exfactory price index to deflate input the variables of technological cluster innovation and use the Data Envelopment Analysis (DEA) Malmquist index to measure the efficiency of provincial technological cluster innovation the base period 2003.
Efficient industrial structure (EF)Efficient industrial structure is a dynamic process, wherein the proportion of high-efficiency industries is continuously increasing and the proportion of poor-efficiency industries is constantly reducing, resulting in gradual industrial intensive development. This study uses the proportion of high-tech industries to represent efficient industrial structure. Therefore, we can construct the following variable, efficient industrial structure (EF).
Where Heit reflects the number of high-tech industry enterprises of provincial region i in the year t. Areait indicates the administrative area of provincial region i in the year t.Pattern of ownership (OS)The efficiency of industrial structure will be affected by the existing pattern of ownership through incentive mechanisms and governance structure (Thomsen & Pedersen, 1998). The newly increased fixed asset investment promotes enterprises’ technological innovation activities. Sufficient investment funds can enhance research motivation and enthusiasm of scientific and technological researchers, increase the output of innovation achievements, stimulate the supply-and-demand structure of the market, and ultimately realize efficient industrial structure. This research uses the newly increased fixed asset investment, accounting for the proportion of the nation's total investment in high-tech industries to measure the pattern of ownership.
Innovative talents gathering (TG)The effects of technological cluster innovation are primarily exerted through independent innovation and technological knowledge accumulation, which drive efficient industrial structure. Improvements in independent innovation ability and the accumulation of technological knowledge are ultimately attributable to the accumulation of innovative talent, which accelerates the process of regional specialization in scientific research and achieves the refinement and specialization of high-end talent (Jiang et al., 2020). Cooperation between industries will be strengthened, affecting the structure of industrial demand and promoting efficient industrial structure. This study selects the proportion of R&D personnel accounted for in the nation's total high-tech industries to measure the innovative talents gathering.
Foreign investment factor (FI)Independent innovation can significantly promote efficient industrial structure. If an enterprise or industry endeavors to stand firm within the national economy, it must obtain intellectual property rights through establishing independent branding and ultimately achieving the goal of new industrialization. To improve the usage efficiency of advanced global scientific and technological elements in dynamic circulation and to enhance enterprises’ cluster innovation capability, it is helpful to digest, absorb, and reinnovate foreign advanced technologies (Stiebale & Reize, 2011). This study uses the proportion of total investment in foreign-invested enterprises to estimate the FI factor.
Spatial Durbin model constructionUnder the influence of connected knowledge spillover, there is a positive effect on efficient industrial structure with the accumulation of technical knowledge and the cooperative innovation of enterprises or industries in the region. The region attracts high-tech enterprises or emerging enterprises through accumulating factors, such as technology, talent, and innovative elements, which promotes industry agglomeration, enhances the cooperative competition effect of enterprises or industries, and ultimately achieves efficient industrial structure. Spatial evolution maps of regional technological cluster innovation and efficient industrial structure indicate that the hierarchical accumulation of technologies or industries leads to the hierarchical agglomeration of emerging technologies and advanced knowledge. The “polarization” phenomenon appears in efficient industrial structure.
The characteristics of spatial dependence and spatial lag of the explanatory variables improve the equation's estimation accuracy, which is increasingly favored by scholars (Elhorst & Fréret, 2009; Greene, 2005). This study constructs a spatial Durbin model to explore the spatial effects of technological cluster innovation driving efficient industrial structure.
where δ is the spatial association coefficient, reflecting the spatial dependence between the dependent variables. Wij measures the row-standardized spatial weight matrix, and c is the constant term. β refers to the unknown parameter vector of the independent variable, primarily explaining the degree and direction of the influence of the explanatory variable on the explained variable. θ represents the parameter vector of order K×1, indicating the degree of influence of the explanatory variables on the explained variable in the neighboring area. μi refers to the individual spatial effect, capturing the individual heterogeneity between the regions. λt is the time effect, indicating the amount of unobservable information received by an individual during a specific period. This study builds the geographical distance spatial weight matrices from the perspective of technology acquisition, technological transformation and upgrade, and independent innovation ability. We then apply the spatial Durbin model constructed to explore the spatial effects of technological cluster innovation driving efficient industrial structure.Model 1, 2, and 3 can be established as follows:
The data of 30 provinces in China (data from Tibet Province are severely lacking, and hence, were discarded) from 2003 to 2017 were selected for an empirical analysis of technological cluster innovation driving efficient industrial structure.4 Data are from the China Science and Technology Statistical Yearbook, China High-Tech Industry Statistical Yearbook, China Statistical Yearbook, China Urban Database, and EPS Database. Missing data are complemented by interpolation of data from the previous and following years.
Results and discussionResults of empirical analysisWe establish a spatial Durbin model from the perspective of technology acquisition, technological transformation and upgrade, and independent innovation ability, exploring the spatial effects of technological cluster innovation driving efficient industrial structure. From the results, the Hausman test value is 28.87 and the p-value is 0.00, which is statistically significant at the 0.01 level. We then construct an individual fixed effect spatial Durbin model. See Table 1 for the descriptive statistics of each variable.
Statistical characteristics of each variable of the model.
| Variables | Sign | N | Max | Min | Mean | SD |
|---|---|---|---|---|---|---|
| Technological cluster innovation | JI | 390 | 1.00 | 0.04 | 0.56 | 0.32 |
| Efficient industrial structure | EF | 390 | 51.75 | 0.02 | 3.20 | 7.83 |
| Pattern of ownership | OS | 390 | 0.32 | 0.00 | 0.03 | 0.05 |
| Innovative talents gathering | TG | 390 | 0.14 | 0.00 | 0.03 | 0.03 |
| Foreign investment factor | FI | 390 | 0.38 | 0.00 | 0.06 | 0.05 |
Here, we apply the maximum likelihood estimation method to estimate Models 1, 2, and 3, obtaining the following empirical results in the China's nationwide and subregions (Tables 2–4).5
Empirical results of model 1.
| Variables | Nationwide | Eastern China | Central China | Western China |
|---|---|---|---|---|
| WLDI * EF | 0.20 * (1.05) | 0.34 *** (3.19) | −0.27 *** (−2.88) | −0.03(−0.35) |
| JI | 1.12 *** (2.89) | 0.48 (0.55) | 0.21 *** (4.7) | 0.05 ** (1.66) |
| OS | 3.96 (0.61) | 1.15 (0.92) | 2.99 *** (3.04) | 1.35 ** (2.31) |
| TG | 1.41 *** (8.03) | 1.66 *** (5.45) | 1.19 *** (6.81) | 0.51(0.67) |
| FI | 1.41 (0.645) | −1.02 * (−1.05) | −0.10 (−0.41) | 0.01 * (1.06) |
| WLDI * JI | 3.09 ** (2.75) | −1.85 * (−1.17) | 0.13 ** (1.46) | −0.08 * (−1.16) |
| WLDI * OS | 4.68 ** (2.86) | 2.57 *** (4.31) | −0.49 (−0.26) | −2.82 (−0.22) |
| WLDI * TG | 1.35 ** (2.91) | −1.89 (−0.86) | 1.50 *** (5.56) | 1.30 ** (1.37) |
| WLDI * FI | 1.51 (0.32) | 2.75 ** (2.69) | −0.01 (−0.01) | −0.09 ** (−1.62) |
| logL | −636.77 | −278.73 | 131.12 | 208.38 |
| R2 | 0.97 | 0.97 | 0.95 | 0.96 |
| σ2 | 2.19 | 4.24 | 0.00 | 0.00 |
Note: * Significance at the p < 0.1 level; ** Significance at the 0.05 level; *** Significance at the 0.01 level. The t-value is in parentheses.
Empirical results of Model 2.
| Variables | Nationwide | Eastern China | Central China | Western China |
|---|---|---|---|---|
| WLDR * EF | 0.07 (0.867) | 0.31 *** (3.21) | −0.12 (−0.97) | −0.13 (−0.25) |
| JI | 0.99 ** (2.645) | 1.00 * (1.13) | 0.21 *** (4.49) | 0.06 ** (1.67) |
| OS | 1.42 * (1.07) | 1.40 * (1.08) | 3.34 *** (3.61) | 1.38 ** (2.35) |
| TG | 1.67 *** (9.38) | 2.04 *** (6.50) | 1.92 *** (7.43) | 1.13 (0.78) |
| FI | 2.01 (1.01) | 4.50 (0.89) | 2.07 ** (2.30) | −0.08 (−0.70) |
| WLDR*JI | 2.32 ** (2.67) | −0.43 (−0.35) | 2.21 ** (2.38) | −0.08 ** (−1.56) |
| WLDR*OS | −3.67 *** (−3.92) | 3.07 *** (4.42) | −0.62 (−0.32) | 2.29 * (1.12) |
| WLDR*TG | −6.28 *** (−3.86) | −1.47 ** (−1.96) | 3.47 *** (6.43) | 1.05 (0.69) |
| WLDR*FI | 1.59 * (1.656) | 3.445 *** (3.63) | −1.22 (−0.55) | −1.35 * (−1.25) |
| logL | −484.06 | −280.20 | 136.25 | 208.47 |
| R2 | 0.97 | 0.97 | 0.95 | 0.96 |
| σ2 | 2.08 | 4.32 | 0.00 | 0.00 |
Note: * Significance at the p < 0.1 level. ** Significance at the 0.05 level. *** Significance at the 0.01 level. The t-value is in parentheses.
Empirical results of Model 3.
| Variables | Nationwide | Eastern China | Central China | Western China |
|---|---|---|---|---|
| WLDZ * EF | 0.13 ** (1.64) | 0.13 * (1.27) | 0.28 ** (2.47) | −0.05(−0.43) |
| JI | 1.82 ** (2.53) | 2.60 (0.63) | 0.22 *** (4.83) | 0.07 ** (1.96) |
| OS | 1.03 ** (1.81) | 1.54 (1.06) | 3.69 *** (3.83) | 2.99 ** (1.87) |
| TG | 1.74 *** (9.99) | 2.89 *** (5.58) | 1.71 *** (6.67) | 1.50 (0.75) |
| FI | 2.76 (0.87) | 5.72 (0.56) | 3.23 * (1.06) | −0.10 (−1.03) |
| WLDZ * JI | 2.08 *** (3.22) | 1.40 (0.94) | 0.22 ** (2.35) | −0.15 ***(−3.60) |
| WLDZ * OS | 3.80 * (1.11) | 5.80 (0.81) | −2.31 * (−1.05) | 1.87 *** (5.38) |
| WLDZ * TG | 6.51 * (1.04) | −4.65 (−0.62) | 2.81 *** (5.44) | 1.71 * (1.19) |
| WLDZ * FI | 7.45 ** (2.32) | 3.09 *** (3.02) | −0.13 (−0.38) | −0.17 * (−1.12) |
| logL | −581.36 | −288.62 | 133.91 | 224.10 |
| R2 | 0.98 | 0.97 | 0.95 | 0.97 |
| σ2 | 1.61 | 5.02 | 0.00 | 0.00 |
Note: * Significance at the p < 0.1 level. ** Significance at the 0.05 level. *** Significance at the 0.01 level. The t-value is in parentheses.
According to the estimation results of the individual fixed effects spatial Durbin models, we can observe two notable findings. First, the coefficients of technological cluster innovation, pattern of ownership, innovative talents gathering, and FI are predominantly and significantly positive, indicating a significant positive relationship among these variables and efficient industrial structure under connected knowledge spillovers. This is consistent with the results regarding technological innovation and FI of Wu & Liu (2021). Take Model 1 as an example, when technological cluster innovation changed by 1%, the efficient industrial structure in the nationwide changed by 1.12% in the same direction. Technological cluster innovation improves industrial efficiency by changing the innovation model of enterprises or industries and promotes efficient industrial structure. At a 1% significance level, for every 1% increase in the pattern of ownership, the efficient industrial structure in the Central China increased by 2.99%, and the rest of the regions showed positive changes. Promotion of the pattern of ownership accelerates the development of regional high-tech industries, increases the proportion of high-tech industries in the region, and promotes the accumulation of enterprises in high-tech industry regions. When innovative talent gathering changed by 1%, the efficient industrial structure in the nationwide increased by 1.41% at a 1% significance level. Innovative talents gathering increases the proportion of technical innovation talent, the collective potential of which can be better tapped into and released. The efficient transformation of knowledge to technology can be realized and enterprises will gradually improve their competitiveness, both of which promote efficient industrial structure. When foreign investment changed by 1%, the efficient industrial structure in the nationwide increased. The increase of FI factors will help regional enterprises or industries to better introduce, digest, and absorb advanced foreign technologies and management methods. A large amount of professional talent will be cultivated to service enterprises, strengthening regional independent innovation ability. Regional industrial efficiency will be improved to achieve efficient industrial structure. The abovementioned measures improve the demand for regional technological innovation, transform the regional industrial structure, and advance the achievement of efficient industrial structure.
Second, under the impact of technological cluster innovation, pattern of ownership, innovative talents gathering, and FI factors in the three models, an overall phenomenon emerges, which is that the effect of Model 1 is smaller than that of Model 2, which is smaller than that of Model 3. This indicates that the spatial effect from technology introduction is smaller than that from technical transformation and upgrade, which is smaller than the effect from independent innovation capability. This phenomenon indicates that the process of introduction, digestion, absorption, and reinnovation of foreign advanced technology is the most effective approach for driving efficient industrial structure. In the everchanging state of science and technology transformation, the constraints of resources and environment are increasingly strengthened. Enterprises in a region must face the dual international competitive pressure of continuous technological upgrade and technological innovation. The problem of weak independent innovation has become the bottleneck in China's regional development; therefore, commitment toward independent innovation is the focus of China's future efforts. The process of digesting, absorbing, and reinnovating advanced technologies will help to fully leverage existing global technological stock and strengthen the internal driving force of technological innovation in provinces. Subsequently, the motivation for technological innovation in China will be enhanced, and efficient industrial structure in the region will be promoted.
Additionally, this study explains the effect of independent variables on dependent variables. We unravel the spatial effects of technological cluster innovation driving efficient industrial structure to understand the differences among different variables. From the perspective of the direct and indirect effects, we examine the effect of each indicator on efficient industrial structure, taking the nationwide case as an example. This is shown in Table 5.
Direct and indirect effects of the spatial Durbin model. (Nationwide).
| Variables | Direct Effects | Indirect Effects | ||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | |
| JI | −1.12 *** (−3.03) | −0.99 ** (−2.72) | 0.78 ** (2.41) | −3.09 ** (−2.74) | −2.38** (−2.57) | −2.22 *** (−3.06) |
| OS | −4.10 (−0.61) | −2.60 (−0.37) | −1.11 ** (−1.91) | 4.65 *** (2.77) | 3.99 *** (3.74) | −4.75 * (−1.21) |
| TG | 1.41 *** (7.63) | 1.62 *** (8.92) | 1.43 *** (9.26) | −1.34 ** (−2.73) | −6.59 *** (−3.79) | −7.24 *** (−8.66) |
| FI | −1.32 (−0.60) | 2.09 * (1.07) | −1.69 (−0.82) | 1.53 (0.33) | 1.93 (0.84) | 8.38 ** (2.37) |
Note: * Significance at the p < 0.1 level. ** Significance at the 0.05 level. *** Significance at the 0.01 level. The t-value is in parentheses.
The coefficients of the direct and indirect effects of technological cluster innovation driving efficient industrial structure are predominantly negative nationwide as well as in eastern, central, and western China. This indicates that technological cluster innovation will weaken the spatial spillover effect of efficient industrial structure in the region and inhibit the efficiency of industrial structures in other regions. The main reason for this weakness is that technological cluster innovation drives efficient industrial structure, revealing a significant backwash effect. A basic feature of technological cluster innovation is the accumulation of technical knowledge, whereas its core is the accumulation of talent. A region's technology accumulation has significant effects on economic scale, constantly attracting technology and talent from surrounding underdeveloped areas and generating an inhibitory effect on industrial structure optimization and upgrade in the less-developed surrounding regions, leading to the emergence of negative spillover effects. Additionally, there is a diffusion effect of technological knowledge in developed regions and less-developed regions; that is, developed regions and the surrounding less-developed regions can produce spillovers of technological knowledge through economic and technological exchanges between enterprises. Less-developed regions will be affected by driving and demonstration effects from developed regions and then the positive spillover effects of knowledge and technology will appear; however, the backwash effect of technological cluster innovation is greater than the diffusion effect. The diffusion effect is offset, weakening its influence from technological cluster innovation and resulting in a negative effect on the efficient industrial structure of other regions. Additionally, whether the spillover effect is direct or indirect, technological cluster innovation from the perspective of independent innovation capability has the largest effect on the efficient industrial structure model, indicating that regions should continuously improve and strengthen independent innovation capability, enhance its core competitiveness, and promote efficient industrial structure.
Robust testTo ensure the robustness of the spatial Durbin model, this study will further test the robustness of the empirical results by reducing the indicators (removing indicator FI). The results (Table 6) are below (taking Model 1 as an example).
Results of the robustness test.
| Variables | Nationwide | Eastern China | Central China | Western China |
|---|---|---|---|---|
| WLTZ * EF | 0.00 * (1.26) | 0.29 ** (2.66) | 0.27 ** (2.93) | 0.03 (0.34) |
| JI | 1.09 ** (2.81) | 0.14*(1.16) | 0.21 *** (5.03) | 0.05 ** (1.67) |
| OS | 3.74 (0.58) | 11.05 (0.87) | 3.00 *** (3.21) | 1.34 ** (2.29) |
| TG | 1.41 *** (8.01) | 1.57 *** (5.13) | 1.91 *** (7.30) | 3.83 (0.73) |
| WLTZ * JI | 2.95 ** (2.68) | −4.04 ** (−2.96) | −0.14**(−1.60) | 0.08*(1.24) |
| WLTZ * OS | 5.08 *** (3.22) | 2.37 *** (3.86) | 1.06 (0.75) | 4.62 (0.38) |
| WLTZ * TG | 1.30 ** (2.87) | −6.40 (−0.61) | 3.54 *** (5.96) | 2.56 * (1.12) |
| logL | 637.25 | 283.10 | 130.98 | 208.20 |
| R2 | 0.97 | 0.97 | 0.95 | 0.96 |
| σ2 | 2.19 | 4.56 | 0.00 | 0.00 |
Note: * Significance at the p < 0.1 level. ** Significance at the 0.05 level. *** Significance at the 0.01 level. The t-value is in parentheses.
The positive and negative coefficients of each variable in Table 6 are largely consistent with the results shown in Table 2, indicating that the spatial Durbin model constructed in this study is robust.
In the estimation process, the model may have endogenous problems caused by two-way or reverse causal relationships. For example, the inconsistent institutional quality of a region could hinder the process of advancing efficient industrial structure; thus, the instrumental variable method is selected to address this. The instrumental variable must be uncorrelated with the perturbed term of the interpreted variable and be highly correlated with the endogenous explanatory variable. This study constructs the instrumental variable for geographical distance ([WLDZ2JI,WLDZ3JI]) and the instrument variable for technological distance ([WLTZ2JI,WLTZ3JI] (Alvarez & Arellano, 2003). The above analysis indicates that the influence effect of the connected knowledge spillover spatial weight matrix is the most significant in terms of independent innovation capability; therefore, we choose Model 3 for the endogenous test, taking Model 3 as an example (Table 7).
Endogenous testing of Model 3.
| Variables | Nationwide | Eastern China | Central China | Western China |
|---|---|---|---|---|
| Constant | −8.96 (−1.03) | −16.76*** (−3.00) | −0.62 (−0.11) | 0.09 (0.07) |
| WLDZ * EF | 0.56 (0.94) | 3.44 *** (3.60) | 0.37 *** (3.21) | 0.07 (0.04) |
| JI | 2.35 (0.94) | 4.89 ** (1.68) | 0.07 (0.07) | 0.02 (0.06) |
| OS | 5.12 *** (7.39) | 7.21 * (1.05) | 3.88 * (1.29) | 3.79 *** (3.58) |
| TG | 9.60 ** (1.41) | 1.45 ** (2.23) | 1.34 ** (1.77) | 5.05 (0.89) |
| FI | 7.56 *** (5.76) | 7.62 *** (2.11) | 1.34 (0.35) | −0.39 * (−1.27) |
| WLDZ * JI | 1.64 ** (1.60) | 5.21 *** (3.34) | −0.71 (−0.15) | −0.10 (−0.09) |
| WLDZ * OS | 5.09 *** (4.23) | −4.46 *** (−8.93) | 6.73 ** (2.93) | 4.66 *** (7.07) |
| WLDZI * TG | −1.12 *** (−6.00) | 1.57 *** (8.42) | −4.36 *** (−6.94) | 3.80 *** (8.77) |
| WLDZ * FI | −1.45 *** (−9.74) | 7.10 ** (2.17) | 2.13 ** (1.90) | −0.20 (−0.41) |
| F | 70.59 | 55.91 | 25.38 | 41.50 |
| Sargan | 12.15 *** | 1.53 * | 1.09 * | 0.77 ⁎⁎ |
Note: * Significance at the p < 0.1 level. ** Significance at the 0.05 level. *** Significance at the 0.01 level. The t-value is in parentheses.
The result in Table 7 demonstrates that all instrumental variables pass the Sargan test, and the positive and negative levels of each variable remain consistent with previous results. This further verifies that technological cluster innovation under the spatial weighted matrix of connected knowledge spillover from the perspective of geographical and technological distance has a positive effect on efficient industrial structure.
ConclusionsIn the context of the knowledge economy and economic globalization, knowledge, information, and technology continue to overflow, transform, and exchange in multiple ways between enterprises and industries, promoting the upgrade and optimization of the industrial structure. As the backbone and key driving force for the optimization and upgrade of the industrial structure, technological innovation has always played a role of changing the industry ratio and transforming the industrial demand structure. Improvement in technological innovation capabilities generated by knowledge spillovers has become the main approach for advancing the optimization and upgrade of industrial structure. Based on existing theoretical models, this study selects China's provincial data from 2003 to 2017 and constructs a spatial Durbin model to deeply analyze the spatial effect of technological cluster innovation driving efficient industrial structure under connected knowledge spillovers. The following conclusions can be drawn from this study.
First, provinces with strong technological cluster innovation capability have evolved from the eastern region to the central and western regions. A remarkable polarization phenomenon appears in China's regional efficient industrial structure. Second, there is a significant positive correlation among regional efficient industrial structure and technological cluster innovation, pattern of ownership, innovative talents gathering, and FI. Technological cluster innovation improves industrial efficiency by changing the innovation model of enterprises or industries. The promotion of the pattern of ownership increases the proportion of high-tech industries in a region. Gathering of innovative talent and increased FI enhance industrial competitiveness from the perspectives of human capital and financial resources, respectively. These measures contribute to the achievement of efficient industrial structure. Third, in the context of connected knowledge spillovers, the spatial effect of technology introduction is smaller than that of technical transformation and upgrade, which is smaller than that of independent innovation capability. This implies that introducing, digesting, absorbing, and reinnovating advanced foreign technologies are effective approaches to drive efficient industrial structure. Independent innovation capability is the ultimate growth driver for efficient industrial structure. Fourth, technological cluster innovation will reduce the spatial spillover effect of efficient industrial structure in a region; therefore, the efficient industrial structure of neighboring regions will be negatively affected. A region's technology accumulation has significant effects on economic scale, constantly attracting technology and talent from the surrounding underdeveloped areas and producing an inhibitory effect on the optimization and upgrade of the industrial structure in the less-developed surrounding regions, leading to the emergence of negative spillover effects.
Based on our research conclusions, the following suggestions may be helpful for decision makers both from the supply side (government) and demand side (enterprises) in promoting efficient industrial structure. (1) Preferential policies for the development of the central and western regions should be released continuously, promoting the transfer of industrial resources from the eastern regions to the central and western regions. In addition, the backward infrastructure construction is also an important factor restricting their development. The development status of the basic industries should be improved through preferential policies, creating a good external environment for attracting foreign investment and technological innovation talents, and finally realizing the coordinated development in the nationwide. (2) Based on the development of technological innovation in China, the government should prioritize encouraging cooperation between organizations, such as technical achievement transformation enterprises, talent exchange organizations, and intermediaries. Connected knowledge spillovers will be strengthened through cooperation and a complementarity effect among enterprises, which promote efficient industrial structure. The government and other relevant departments should strengthen the construction of regional technology innovation bases to form industrial clusters, emphasizing technology embedded innovation, technology integration innovation, and technology cluster innovation. Regional effects of economies of scale and scope should be realized, enhancing the international competitiveness of industries. (3) Enterprises should gather technological innovation resources, basic and leading-edge technological research achievements, and other innovation factors to strengthen the dominant position of independent innovation. Enterprises’ innovation will be cultivated through the force of synergy, improving the technological innovation capability of high-tech enterprises. On the international side, building an information network for the transformation of technological innovation achievements will help to achieve knowledge sharing at different stages of technological innovation, accelerate the flow rate of technological innovation achievements in the transformation system, and minimize technological innovation risks and cost. The efficiency of regional technological innovation will be improved and the international technological innovation environment will be optimized. (4) The agglomeration of high-tech knowledge will help strengthen the endogenous power of enterprises. It uses technology, knowledge, and talents as the link of interaction to achieve efficient interaction between the innovation chain and the industrial chain. Enterprises should gather their own technological innovation resources, basic research results and frontier research, cultivating innovation mechanism through synergistic forces, and ultimately enhancing the endogenous growth momentum. The optimization and upgrading of the industrial structure will be promoted fundamentally.
With the advancement of knowledge structure and scientific research methods, research will be conducted on the following issues in the future. (1) More systematic theoretical hypotheses and empirical analysis on technological cluster innovation driving efficient industrial structure from the perspective of spatial characteristics. Future research can examine the problem from a broader perspective to draw additional novel conclusions. (2) From the perspective of theory and empirical research, future research could explore the internal mechanism and main sources of the reverse technological spillover in technological innovation and analyze how technological innovation affects the optimization and upgrade of regional industrial structure through technological spillover. (3) According to regional characteristics in the world, a differentiated evaluation system could be established to further explore the regional mechanisms of internal influence.