As the world is fighting against the continuous spread of the COVID-Sars-2 virus and the consequences the pandemic has brought about on economic, political and societal levels, the emergence of the vaccination programs seems to be the biggest hope for a quick return to, popularly called, the “new normal”.
As it is not feasible to vaccinate at the same time the whole population, the states, provinces and cities had arranged – though, admittedly, taking into consideration limited numbers of criteria - homogenous groups of citizens, who, labelled as “risk groups”, have been chosen as those who will be receiving the vaccination before others, adding to the already existing feelings of chaos and shortage.
We want to address the issue that despite the access to the expertise and knowledge of intradisciplinary committees, we still do not have a satisfactory answer regarding the further steps for the vaccination programs. We believe it is due to the persistence of the binary way of reasoning, with its tendency to overlook the complexity of the issue and emphasize objectivity while neglecting the subjective factors that cannot be easily quantified.
For that very reason, we propose the application of the theories of uncertainty with the support of the fuzzy subset theory, which will result in the creation of the humanist algorithms of clustering of populations, allotment of different kinds of vaccine for diverse persons in the groups and, finally, ranking for the priority of vaccination. This approach will allow designing a vaccination model to that will allow to maintain, to the highest possible level, the principles of ethics, morale and solidarity, and efficiency and effectiveness.
From early 2020 and until now, the world has been brought to a halt due to the COVID-19 pandemic. The economic, educational, social, and human costs, not to mention those for health and health systems, are difficult to grasp. As of mid-April of 2021, the World Health Organization (WHO) has reported over 3 million deaths worldwide and 76,882 in Spain alone (World Health Organization, 2021). The health workers and health systems in nearly every country have been stretched to their limits (Pillai et al., 2020). The national economies are suffering, businesses (especially small and medium-sized ones) are reporting record levels of bankruptcy, and the unemployment rates keep growing (Abel & Gietel-Basten, 2020; Brodeur et al., 2020). In the of the European Union, the countries whose economy relies heavily on tourism, such as Italy, Greece or Spain, are in a particularly difficult situation. To give an example, the Spanish economy has reported a shrunk of 11% in 2020 and growing unemployment rates of 19% (Georgiou, 2021). We will have to wait longer in order to get the picture of the of the psychological toll of the situation – confinement, separation from families and peers, growing rates of domestic violence, depressions and suicides, as well as overwork and work under constant stress are just some of the examples of the price that the world will be paying (McIntyre & Lee, 2020; Usher et al., 2020).
Despite this rather pessimistic description, we ought to remember that this is not the first time we have found ourselves in dire situations like this. The outbreak of influenza at the end of the First World War, confusingly and mistakenly labelled as Spanish flu, even though it originated most probably in the USA, infected a fifth of the world population and caused deaths of estimated 20–50 million (!) people (Hays, 2009; Trilla et al., 2008). This data is highlighted not to diminish the importance and graveness of the current situation but rather to draw attention to the ‘advantages’ we now ‘enjoy’ thanks to the sacrifices (especially those of the health care workers) and scientific achievements of the modern world – the vaccine.
Although we constantly keep learning about the new virus and its possible mutations (Fauci et al., 2020), the last hundred year's scientific progress in fields of medicine, virology, sanitation and hygiene, not to mention human rights and equality, has put us ahead when compared with the influenza crisis of 1918. It has to be noted that the ‘record’ time in which the vaccines have been designed, procured and produced on the industrial, together with the heroism of the health care workers, is short of a miracle(Graham, 2020). We are starting the final stage of the vaccination process – the vaccinations of individual citizens, all done to achieve herd immunity, stop the rapid spread of the virus and all its consequences – first, deaths and later, the possibility for the economic revival. However, we are still at the early stages of that process. As of the 24th of April 2021, only 3% of the world population has been fully vaccinated (Our World In Data, 2021). In Spain, the number reaches 8.2% (Ministerio de Sanidad, 2021). We are facing the expected challenges: lack of health care workers needed for vaccine administration, the existence of different kinds of vaccines that are thought more appropriate for a particular group(s) of people (Mills & Salisbury, 2021), and the obvious obstacle of not being able to immunize the whole population at the same time, which causes the general feeling of shortage.
These obstacles have led to different approaches in different countries and parts of the world. First, when it came to the so-called group 0, the front runners of the fight with the pandemic – mainly health care and sanitary workers – were given (and rightly so) the priority to receive the first available shots. However, when it came to the following stages of vaccination processes, the procedures adopted gave the impression of being chaotic and 'a guess work'. When 'selecting' who should receive the jabs before the others, the main criteria have been usually based on age, occupation, and the candidate's medical history (Clínica Barcelona, 2020). Hence, it is of pivotal importance to find 'correct' ways of clustering, allocation, and ranking of the homogenous groups for the correct type of vaccine for populations residing in a given territory (e.g., Spain, Catalonia, Barcelona…). We want to propose a 'method' to obtain a homogenous clustering of groups of people, with the correct allocation of the existing type of vaccines and establishing the priority within every homogenous group obtained. What is crucial is that, while doing so, we maintain, to the highest possible level, the principles of ethics, morals and solidarity, and efficiency and effectiveness (efficacy).
2Literature review and theoretical frameworkWith the beforementioned shortage of medical staff and the vaccines themselves, it does not seem too difficult to appreciate the difficulty of making decisions regarding the ‘order’ in which the vaccines should be administrated (Tran et al., 2020), as prioritizing one citizen over another translates to, in a sense, ‘depraving’ the other.
It seems reasonable to ponder whether the priority for vaccines should be given to those who need them most or to those who are the most vulnerable. We strongly believe that both of these aspects should be considered (Haynes et al., 2020). However, as was mentioned before, the process of finding homogeneous clusters, allotting the correct vaccine, and establishing the order of the priority of vaccination should be based not only on a strictly ‘medical’ basis. It should also include the social and economic aspects without neglecting the principle of solidarity in the process. The level of ‘importance’ of these added aspects can differ (or not) for every single one of them. The ongoing research finds an association with the higher risk of COVID-19 infection not only dependent on age. The socioeconomic position, living conditions, job position within the institution, biological sex, and race and gender seen as socially constructed must be acknowledged (Gausman & Langer, 2020; Mutambudzi et al., 2021; Nabe-Nielsen et al., 2021).
As it is a matter of extreme importance (and it is also extremely time-sensitive), and as most of the countries have established Interdisciplinary Committees with epidemiologists, doctors, biologists, jurists, economists, and social workers, among others, to solve the issue, we need to ask why are we still not having a satisfactory solution to this global problem of the utmost importance?
We are convinced that the existence of those committees is necessary, but we also believe that their primary role should be ‘corrected’. It happens very often that works of popular opinionmakers or famous names finish at the point when the real investigation should begin, and, what is more, the ‘results’ are being taken as granted, without reflection or even stopping for thinking about the tools applied (Rapport, 2002). We wish to alternate those scenarios with the aid of the new theories of uncertainty (Zinn, 2009), supported with the fuzzy subsets theory (Zadeh, 1965, 1996; (Gil-Aluja, 2001)). We propose to turn to non-numerical mathematics, which – while breaking with the limitations of binary logic (Kosko & Isaka, 1993) – will allow us to take into consideration objectively quantifiable variables, as well as subjective ones. By doing that, we should create a tool that can be constantly (and efficiently) adjusted to the circumstances and any arising ‘new’ uncertainties (Gil-Aluja, 2001)).
To be more precise, we would like to present the elaboration of three humanist algorithms: of the clustering of homogenous groups based on shared characteristics and exposure to the risks (Gil-Aluja, 2001)), of the allotment of different kinds of vaccines for previously established clusters, and, finally, of the ranking of priority of the clusters. It is essential to highlight that the humanist algorithms, derived from the fuzzy sets and developed with the theories on non-numerical mathematics, has previously produced outstanding results in solving issues associated with, for example, migration and refugee crisis (Gil-Aluja, 2020), kidney transplants in non-matching donors and receivers (Roth, 2004, 2017) and for the effective management in sports (Gil-Lafuente, 2002).
The flexibility and adaptability of those algorithms make them particularly useful in the moments of rapid change, such as the conditions in which vaccine has to happen: the rise of different mutation of the virus, as well as the changing behaviors of the citizens who are supposed to receive a vaccine both play a key role.
Another advantage of the proposed approach is that it takes into consideration human nature, which usually cannot be explained with the rigid rules of binary logic or statistical analysis. It is of the utmost importance to realize that, while planning for the vaccination priority, we are 'dealing' not only with the management of the pandemic and the virus itself but also that of people, with their 'tendency' of emotional (and more often than not, irrational) decision-making process (Li et al., 2014; Wilson, 2012).
3MethodologyBefore we deploy the algorithm, we are required to solve the problem of the homogeneous clustering of citizens whom, in each group, possess the characteristics established at previously defined levels or degrees.
The selection of the characteristics taken into consideration is a first main task to be assigned to the Interdisciplinary Committees.
Once the characteristics have been assigned, for each of the groups formed to be considered homogeneous, it is necessary to have a transitive property among the citizens of the same group (if citizen A is homogeneous with citizen B and citizen B is homogeneous with citizen C, then A will be homogeneous with C). These relationships then become "similarity" relationships.
The first task for each algorithm consists of obtaining the homogeneous clustering relations; then the relations for assigning the type of vaccine to each group, and, finally, establishing an order of vaccination between the homogeneous groups is found. These relationships are represented using a neural graph (Kaufmann & Aluja, 1995), usually by means of matrices of different nature or using sagittal shapes.
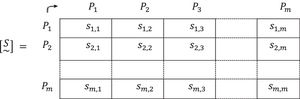
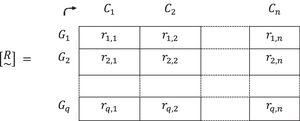
Our first step is to define a fuzzy matrix [R~] built from the definition of the people that make up a general group (city, autonomous community, state) by means of the degree or level of the criteria possessed by each one of them (age, vulnerability, economy, utility, exposure).
These criteria are met in a set E1={Ci,1≤i≤n}, and people residing in a general group would form another set E2={Pj,1≤j≤m}. We define μj,i as the degree or level that person j possesses of criterion i. It is possible to describe each element of the set E2 (people) by means of a fuzzy subset Pj~:
where 0≤μj,i≤1,1≤i≤n,1≤j≤m.The meaning of μj,i can be either names, concepts, criteria, values, or valuations defined by the Interdisciplinary Committees thanks to their experience, training and competences in the disciplines that concern them.
Throughout all the work, the concept of the discrete fuzzy sets based on the notations proposed by Kaufmann and Aluja (1995) has been used. We start from a family of functions belonging to μi:E2→[0,1],1≤i≤n, where μi(Pj)=α, if α is the degree or level that person Pj possesses of criterion Ci. Then, from μi,1≤i≤n, function μ:E2→[0,1]n is build, defined by:
To ease the notation, we simplify μi(Pj) as: Then, each person is characterized by an n-dimensional vector whose components represent the degree level at each criterion, that is:3.1Algorithm for clustering of the homogenous groupsIt is important to recall that clustering, to qualify as homogeneous, must fulfill, in the field of fuzziness, certain properties: symmetry and reflexivity, but also transitivity. The first two provide relationships of likeness, the third provides a relationship of similarity.
In binary algebra, some algorithms that allow obtaining maximum similarity sub-relations have been developed. For the development of this algorithm, we will rely on them to achieve the purpose of homogeneous clustering.
As already determined, the information supplied by the Interdisciplinary Committees is the descriptions of the elements of a set E2 of people, by means of fuzzy subsets of the referential of a set of E1criteria that each person possesses in a certain degree or level.
Among the most used algorithms, we have chosen the Pichat (1970) algorithm to perform the homogenous clustering.
The steps of the proposed algorithm are as follow:
- 1.
Establishing the criteria Ci,i=1,2.,…,n to be used for the description of all the people Pj,j=1,2,…,m by forming the sets E1 and E2 respectively. This task corresponds to the Interdisciplinary Committee.
- 2.
Measuring and/or assessing the degree or level of all the criteria possessed by each person constructing the fuzzy subsets, Pj~,j=1,2,…,m. This should be done between the Interdisciplinary Committee and the authors of this work or other researchers in the field of fuzzy sets.
- 3.
Obtaining the relative distances between all the fuzzy subsets that describe all the people taken two by two. If, for example, the relative Hamming distance is chosen, the operation to be used in each pair will be:
6. A minimum level of homogeneity is considered for the groups. For this, a threshold is introduced into the algorithm, that is, a degree or level u such that from it, the affected persons are considered indifferent in terms of the established criteria. This is done for all as:
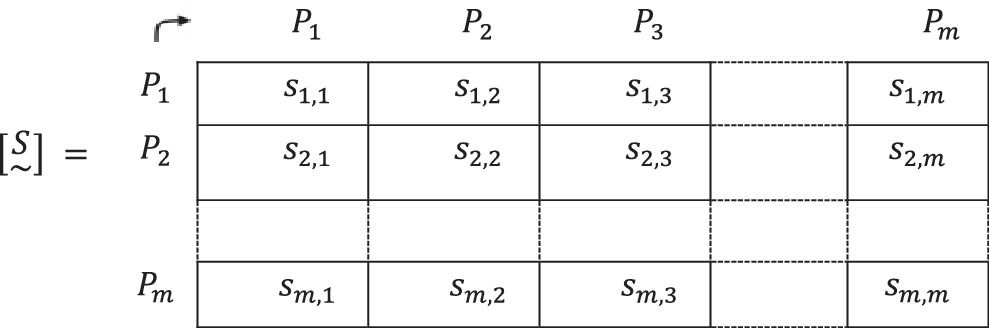
For this work the same threshold u is selected for all the criteria Ci,i=1,2,…,n. There is no problem in selecting the threshold ui, i=1,2,…,n for each criterion. In this case, the opinion of the Interdisciplinary Committee may be of special interest (Kaufmann, 1987; Kaufmann & Aluja, 1993).7. The values sj,k, j,k=1,2,…,n are substituted in the fuzzy matrix [S~] for the bj,k, j,k=1,2,…,m values with which a Boolean matrix [Bu] is obtained.
By reducing the fuzzy matrix [S~] to a Boolean matrix [Bu], “the entropy of the system falls", therefore we should perform this reduction as late as possible (Kaufmann et al., 1994).
This reduction grants a certain degree of flexibility to the algorithm, by which it is possible to change the threshold level, u‐, and to easily establish different thresholds, u1,u2,…,un for each one of the criteria C1,C2,…,Cn. In each case the Boolean matrix would be different.
8. To obtain subgraphs or transitive graphs, the part of the matrix [Bu] located above the main diagonal, inclusive, is considered, by only noting the (empty cells) zeros.
The elements Pj,j=1,2,…,m, (people) of those columns in which there are zeros (empty cells) are multiplied and then the Boolean sum of each element (person) of the corresponding row is carried out, with the product of elements (people) above, for its own row.
9. The Boolean product is made in minimum terms of the previous Boolean sums, considering that:
- (a)
Rows without zeros are excluded from the procedure;
- (b)
When in the result of the product of the sums the repetition of an addend is observed, only one of them is considered, so Pj+Pj=Pj.
- (c)
If in one of the resulting addends includes the same addends as in another, or the same addends are encountered, the one with the greatest number of elements is eliminated. Then:
10. To obtain homogeneous clustering of people as maximum subrelations of similarity, it is needed to proceed from the minimum to the maximum terms by calculating the complement of the reference of E1 (people). Each of these complementary terms is a homogeneous clustering at the u level.
Then, a new set E3 is formed by the homogeneous groups of people Gh,h=1,2,…,q, obtained following the phases of the previous algorithm, always in relation to the established criteria, which is found as sub-relations maxims of similarity.
We represent it as:
Thus, q homogeneous clustering has been formed as follows:It will occur often that a person belongs to more than one group - this will happen when the clusterings are not disjoint. It is important to note that when this circumstance occurs, the decision maker has greater decision-making capability by incorporating one or more criteria to place a person in both groups.
Once the desired homogeneous clustering has been found, it is imperative to establish the most appropriate groups of people for each type of vaccine or, if desired, assign each vaccine to the most appropriate groups. This is valid, both when we are considering the people individually Pj,j=1,2,…,m and when considering the homogeneous groups formed Gh,h=1,2,…,q.
3.2Algorithm for allotment of different kind of vaccinesAs the need to determine with greater precision and rigor which is the most suitable vaccine, there is talk of age ranges, general clinical situation, exposure to contagion and even genes. We consider that all those points should be pondered in a different degree or level and in a greater or lesser importance for each criterion. With the described clustering algorithm, the usage of “fuzzy sets” adequately solves this problem.
For greater generality, it is assumed that the homogeneous clusterings are known, expressed by the q fuzzy subsets Gh,h=1,2,…,q.
For the next phase of the algorithm, we propose the following method:
1. Through Interdisciplinary Committees (with the name they take in each country), we are aware of three groups. Those already used in the previous algorithm: E1 that meets the established criteria Ci,i=1,2,…,n; E3 that contains the homogeneous groups of people found in the previous clustering algorithm Gh,h=1,2,…,q. And to them we added a third set E4 formed by the types of vaccine Vt,t=1,2,…,r.
2. Each type of vaccine is described by means of a fuzzy subset Vt~ of the referential of the criteria Ci,i=1,2,…,n. Expressed as:
where the ϑt,i are the valuations that the Interdisciplinary Committee establishes as adequate for each of the criteria Ci,i=1,2,…,n.
3. Thus, three referential sets are gathered for use in this allocation algorithm: E1, E3 and E4, whose elements are, respectively, the established criteria, the homogeneous groups of people receiving a vaccine and the types of existing vaccines.
4. The level of distance between the needs of each homogeneous group of people and the level possessed by each type of vaccine is calculated, relative to each one of the criteria. A distance operator is usually used. The most frequent is Hamming's relative distance:
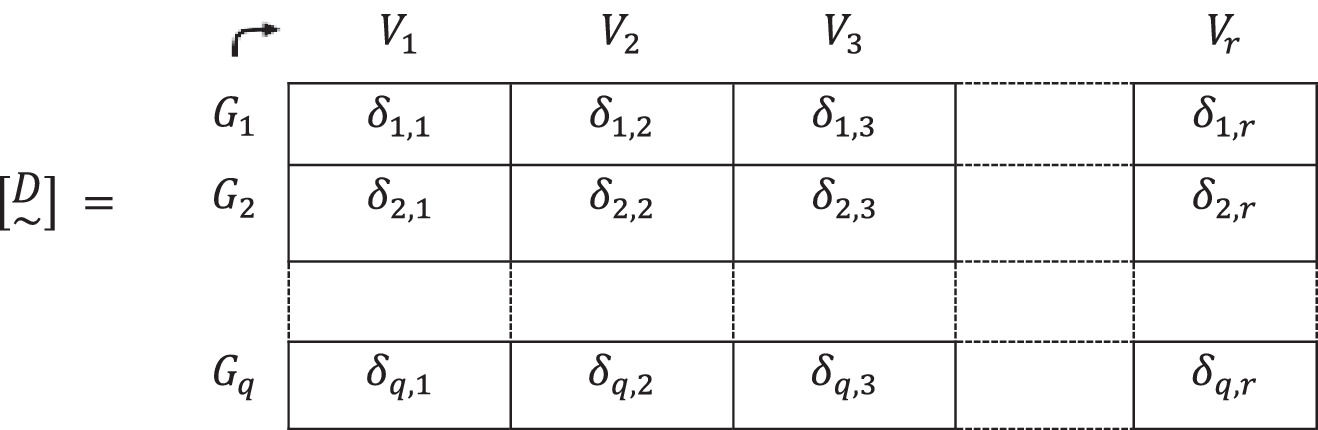
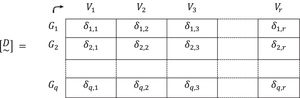
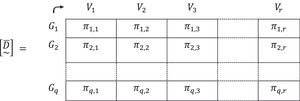
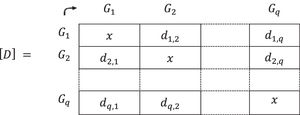
5. The valuations found for the distances that exist between the degree or level possessed by the criteria of each group of people and the one possessed by the different types of vaccines, taking into account the established criteria δ(Gh~,Vt~) will be designated, for convenience, δh,t,h=1,2,…,q; t=1,2,…,r are gathered in a fuzzy matrix of distances [D~]:6. The "neighborhoods" or "proximities", πh,t, are obtained by complementing the unit of the distances already found, that is:
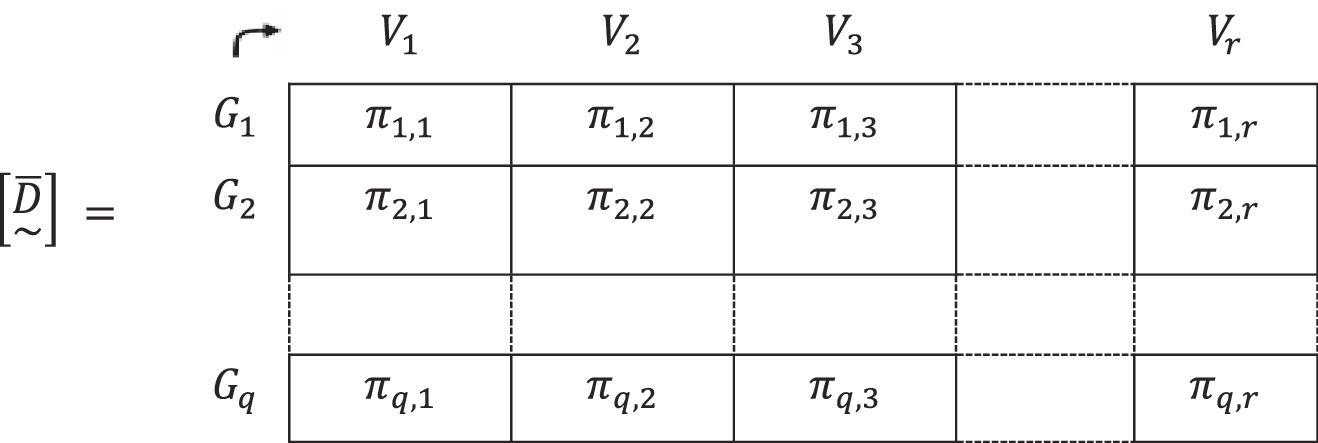
7.- These “proximities” or “neighborhoods” are gathered in a fuzzy rectangular matrix, [D~-]8. In the fuzzy proximity matrix [D~-], the element with the highest valuation, that is, the one that is closest between the “needs” of the group of people and the “answers” that provides the vaccine on the established criteria is chosen.
It is in this element of the fuzzy matrix [D~-] marked by the row and the column to which it belongs, where the group of people from set E3that should receive the vaccine from set E4 is being defined.
If, for example, the closest approach is π7,3 that is:
it transaltes to the group G7 should be vaccinated with the V3 vaccine.9. From the fuzzy matrix [D~-] of order qxr, the row and column to which the highest value of “approach” belongs is eliminated. In the example π7,3 it would be the row 7 corresponding to group G7 and column 3 corresponding to vaccine V3. It then remains, a lower order matrix:
10. The procedure described in phase number 8. would be performed again with the new fuzzy matrix of order (q−1)x(r−1) to find matrices [D~-] of order (q−2)x(r−2), …, and so on until finding all matrixes assigned to q and r.Is important to note that this algorithm is known by its high capacity to be used in the most diverse real situations, generally providing accurate results. However, is plausible that in some special contexts the strict optimum is not reached. In these cases, a partial solution is acceptable (Gil-Aluja, 2001).
When the number of groups of people does not coincide with the number of vaccines, it is possible that one type of vaccine will be applied to more than one group of people. The intrinsic flexibility of the algorithm allows, with slight variations, to vaccinate two or more groups with the same type of vaccine. At the same time, it can also happen that there is some type of vaccine that is not suitable for certain groups of people. In these cases, the committee can determine not to purchase it.
3.3Algorithm for the priority of vaccinationsIn those situations in which the set of people to be sorted does not contain many elements, we proceed to sort them without having to resort to the clustering algorithm. This is not the case of the current vaccination program being studied. We are facing a set made up of millions of elements Pj, j=1,2,…,m (people).
The algorithm can, in general, by means of fuzzy subsets of the referential of the criteria established by the Interdisciplinary Committees, describe both the people Pj, j=1,2,…,m and the homogeneous groups of people Gh,h=1,2,…,q.
An important aspect to be considered is that although in the ordering of people Pj, j=1,2,…,n the evaluations of the degree or level possessed of each criterion by each person can be made directly by the members of the Interdisciplinary Committees, in the ordering of homogeneous groups, it is convenient, when not necessary, to consider the minimum threshold(s) established for each criterion.
To define the algorithm for the priority of vaccination, we will assume that there should be no difficulty in adapting this algorithm to the case of sorting people individually.
We then start from the set E3 formed by the homogeneous groups of people Gh/h=1,2,…,q , whose description takes place through q fuzzy subsets of the referential of the criteria Ci/i=1,2,…,n, to whom the Interdisciplinary Committees have applied minimum thresholds in their grades or levels ui,i=1,2,…,n. Thus, the most general case is approached.
In many works, and adopting a principle of prudence, we assign a degree of possession of any criterion of a group, the level ui, as the minimum that the members of the Interdisciplinary Committee have established when considering it sufficient for the purposes of homogeneity of the group.
We present the algorithm as follows:
1. There are two sets designated by E1, one that meets the criteria Ci,i=1,2,…,n and E2, which is formed by the homogeneous groups Gh,h=1,2,…,q.
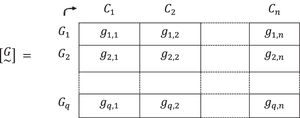
2. Each homogeneous group is represented by a fuzzy subset of the referential of the established criteria:
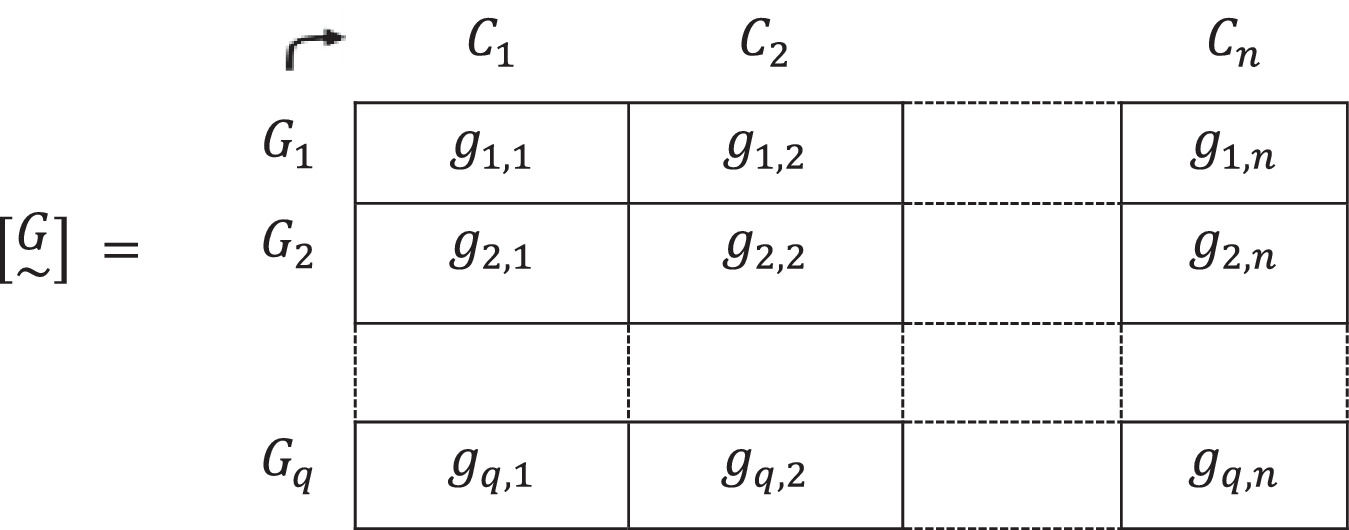
3. These fuzzy subsets are brought together to form a fuzzy matrix [G~] that relates each of the Gh groups with the degrees or levels of all the criteriaCi,i=1,2,…,n. It will be defined as:
At this point, considered two by two, only the relations between the homogeneous groups Gh,h=1,2,…,q, have been established.
Our objective goes further, obviously, since we intend to develop a sorting process considering all the criteria. It is therefore necessary to use an aggregation procedure.
It is at this point where the importance and weight of the criteria must be considered. The first part of the answer must be determined by the Interdisciplinary Committees. Then, their opinions must be transformed into operators.
A particular case occurs if all the criteria have the same importance - that assumption will be addressed later.
For the current approach, the “convex weighting”, well known in the field of determinism, will be used.
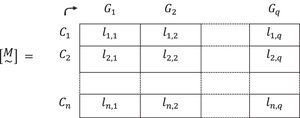
4. “Weight” vectors, [Li~], that represent the degree or level of relative importance of each criterion Ci,i = 1, 2,…, n for each group of people Gh,h=1,2,…,q, are constructed:
5. A normalization by finding a valuation li,h,i=1,2,…,n;h=1,2,…,q , is done, so:
Where the i=1,2,…,n vectors, will be:6. These vectors are gathered in a matrix [M~], such as the following:
Each row of this matrix [M~] expresses the relative importance of each criterion Ci,i = 1,2,…, n, for each homogeneous group of people Gh,h=1,2,...,q.
7. Two matrices are then available: the matrix [G~] that provides the preferred degree or level of all the criteria of all the homogeneous groups of people to be vaccinated, and the matrix [M~] that shows the relative importance that each criterion acquires for each group.
8. By means of the sum-product composition, *, the relative importance of each criterion Ci,i = 1,2,…, n expressed in the matrix [M~] is incorporated into the priorities of each group expressed in the fuzzy matrix [G~].
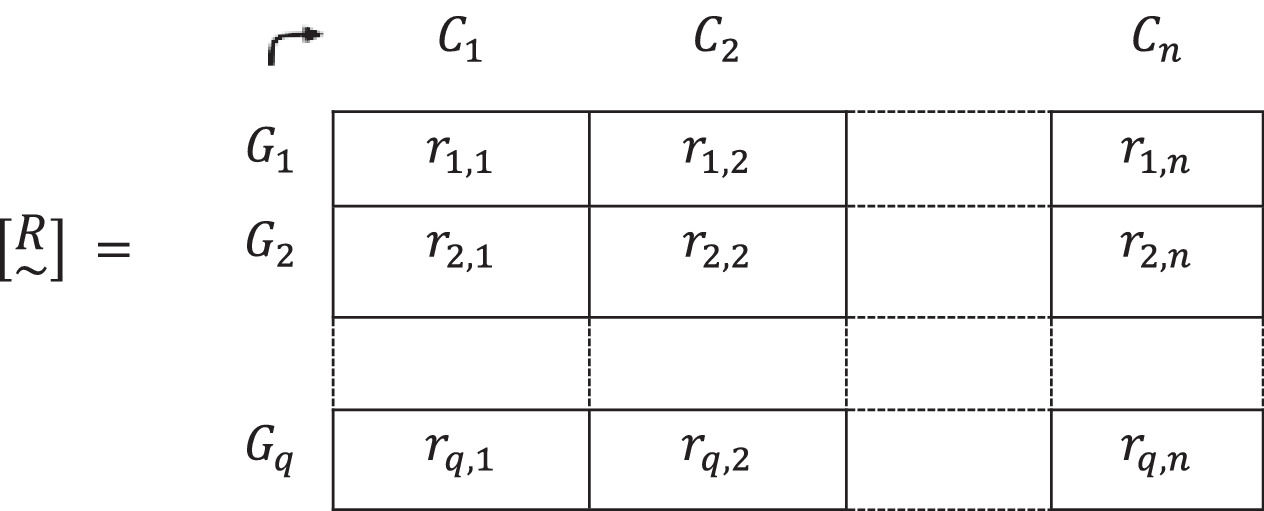
The resulting matrix from the sum-product composition is [G~]*[M~]=[R~], where [R~] is the result of:
It can be represented as:A matrix [R~] that presents by columns the order of preference in vaccination, among all groups Gi,i=1,2,…,q for each criterion Ci,i=1,2,…,n, is obtained. On this occasion, the relative importance of each criterion is already taken into consideration.
9. From the fuzzy matrix [R~], for each of the criteria Ci,i=1,2,…,n a square matrix of order q is found, considering the values of the columns, taken one by one, so that, given, for example, a column
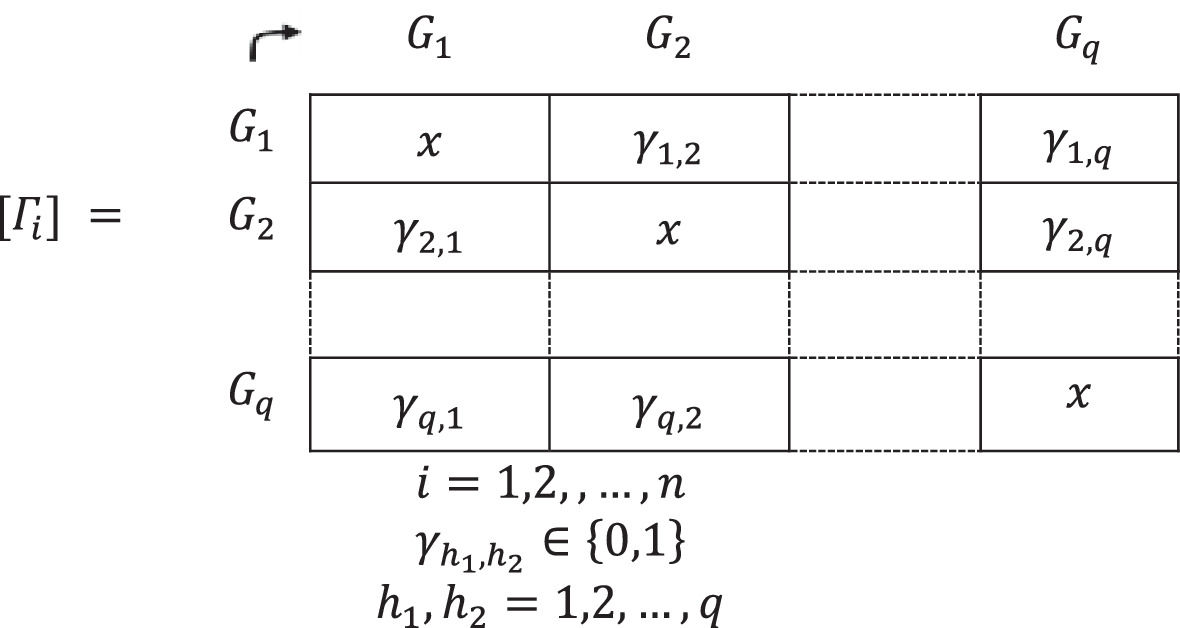
C1, if a 1 is assigned to the cell Gi,Gh when ri,1≥rh,1 and a zero when ri,1 Thus, n Boolean matrices Γi,i=1,2,…,n one for each criterion are found, in which, in both rows and columns, there are homogeneous clustering of people, of the reference E3={G1,G2,...,Gq}.
The valuations, this time binary, {0,1}, now include the relative importance of each criterion. It can thus be said that, in a certain way, a certain “normalization” has been established according to the criteria of the members of the Interdisciplinary Committees. We believe that it is an interesting step forward.
We place an X on each element of the main diagonal to exclude them from the procedure, since it does not make sense to establish a priority between the same group.
10. From the n Boolean matrices [Γi],i=1,2,…,n , which express the priority among the homogeneous groups of people for vaccination Gh,h=1,2,…,q, for each criterion Ci,i = 1,2,…, n, we find the number of criteria Ci,i=1,2,…,n which precedes all the others. This can be done by adding the value of 1 to the relations (G1,G2),(G1,G3),…,(Gq,Gq−1) that appeared in the n Boolean matrices.
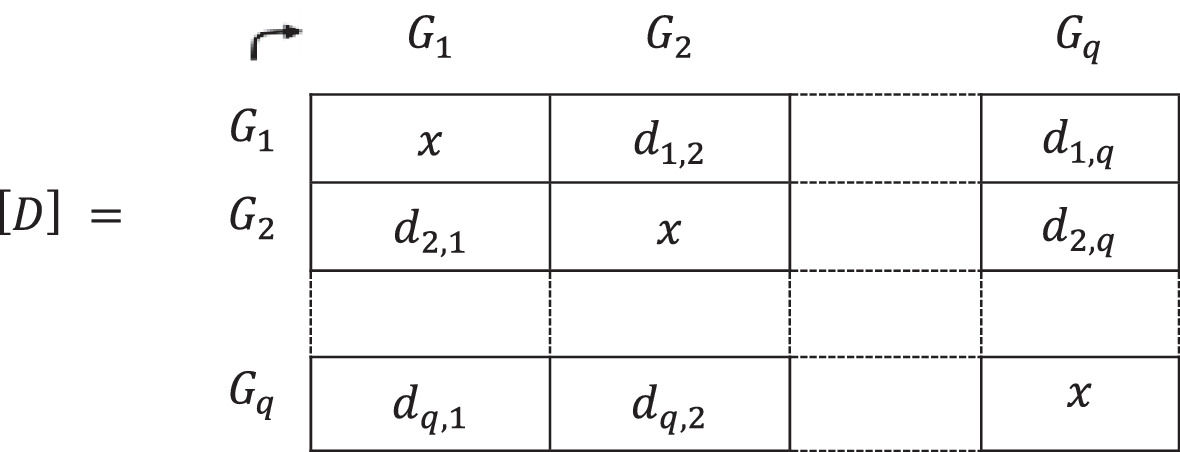
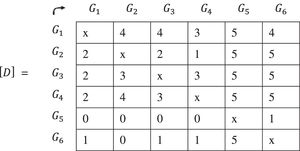
These values are named d1,2Ci,d1,3Ci,…,d1,qCi,…,dq,q−1Ci,i=1,2,…,n and then placed in a matrix [D] with its formative elements:
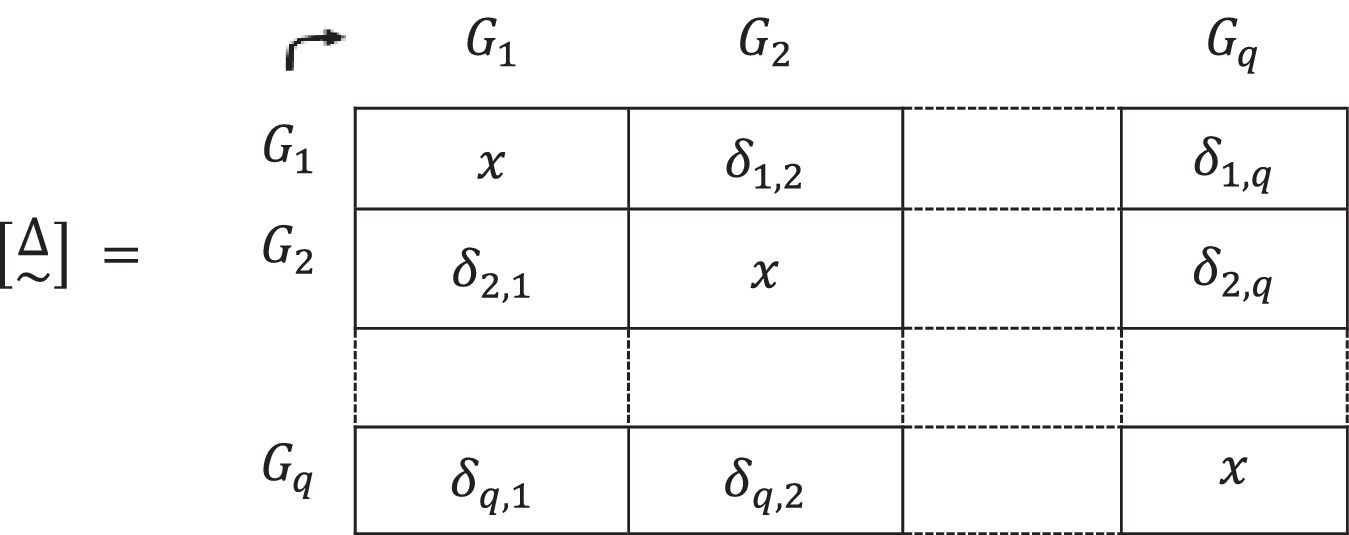
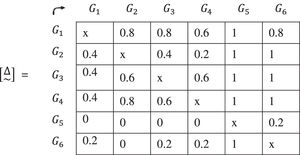
The matrix [D] is obtained, formed by natural numbers resulting from the arithmetic sum of the times that each group precedes another, considering all the criteria, “normalized” by their relative degree of importance. This concept is represented below:11. To continue the investigation operating in the hendecadary system, the matrix expressed in natural numbers [D] is converted into a matrix represented by values in [0,1]. To do this, each element of [D] is divided by the number of criteria, n:
The found matrix [Δ~] is:Once information on the priority of homogeneous groups of people for vaccination is available, in which the importance of each criterion for each group has been considered, the foundations for a solid analysis of these results is laid.
12. There are several paths that we can follow. The one presented in this paper, the decomposition of the matrix [Δ~] into α cuts, has been used on several occasions (Gil-Aluja, 2020; Gil-Lafuente, 2002; Roth, 2017).
Using the hendecadary system, the matrix is decomposed making the cuts at a higher level according to the requirement of a stronger priority. “Normally” the highest α levels are chosen: α1,α0.9,α0.8,α0.7,…
13. Once the cut-off level α has been chosen, the analysis of the arrangement resulting from the matrix found [Δi] is done. The comparative analysis between levels [Δ1],[Δ0.9],[Δ0.8]… is usually very suggestive.
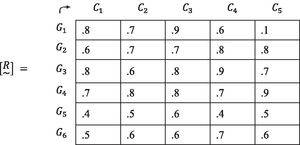
As an example, an assumption (Gil-Aluja, 1999) from phase 8 is reproduced.
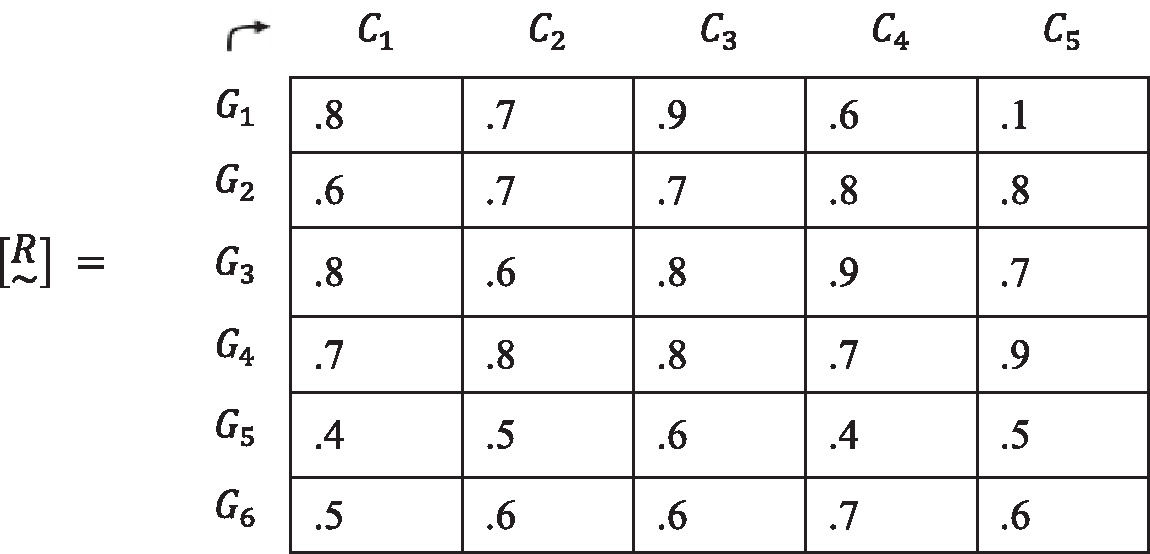
8. The fuzzy subsets come together to form a fuzzy relationship [R~]:
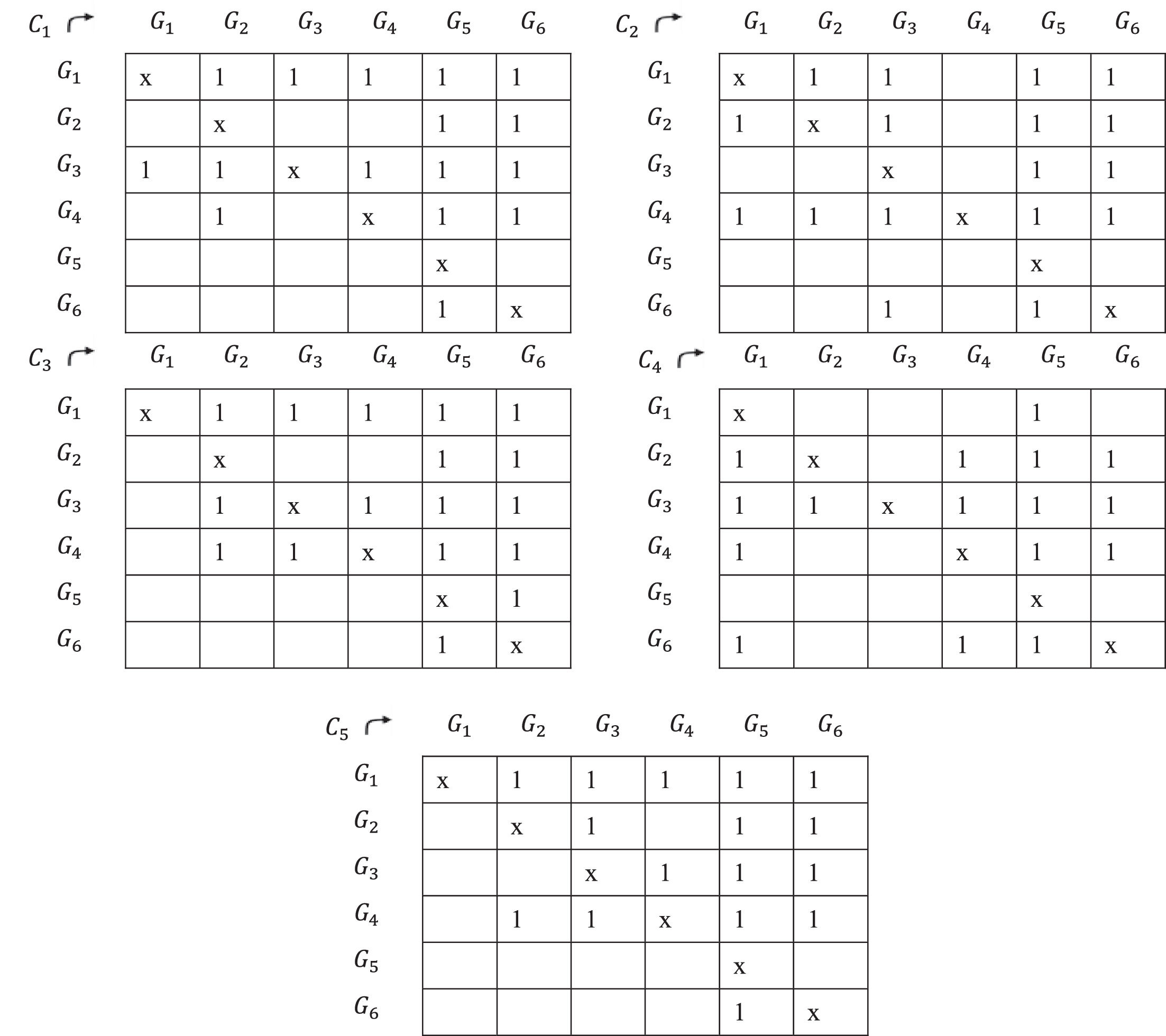
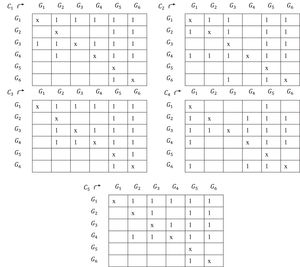
9. Each criterion of the preferences of each group over the others C1,C2,C3,C4,C5 is found. An X is placed in the cells on the main diagonal of the matrices to remove them from the process. When there are equal valuations for several elements in the same column, a 1 will be assigned to both the cell representing the preference of one and that of the other.
Assuming that in a column of the fuzzy relation [R~] the same valuation is not repeated, the Boolean matrix of a criterion will be antisymmetric. In the current example, this only happens in the matrix corresponding to G5 (the last one).
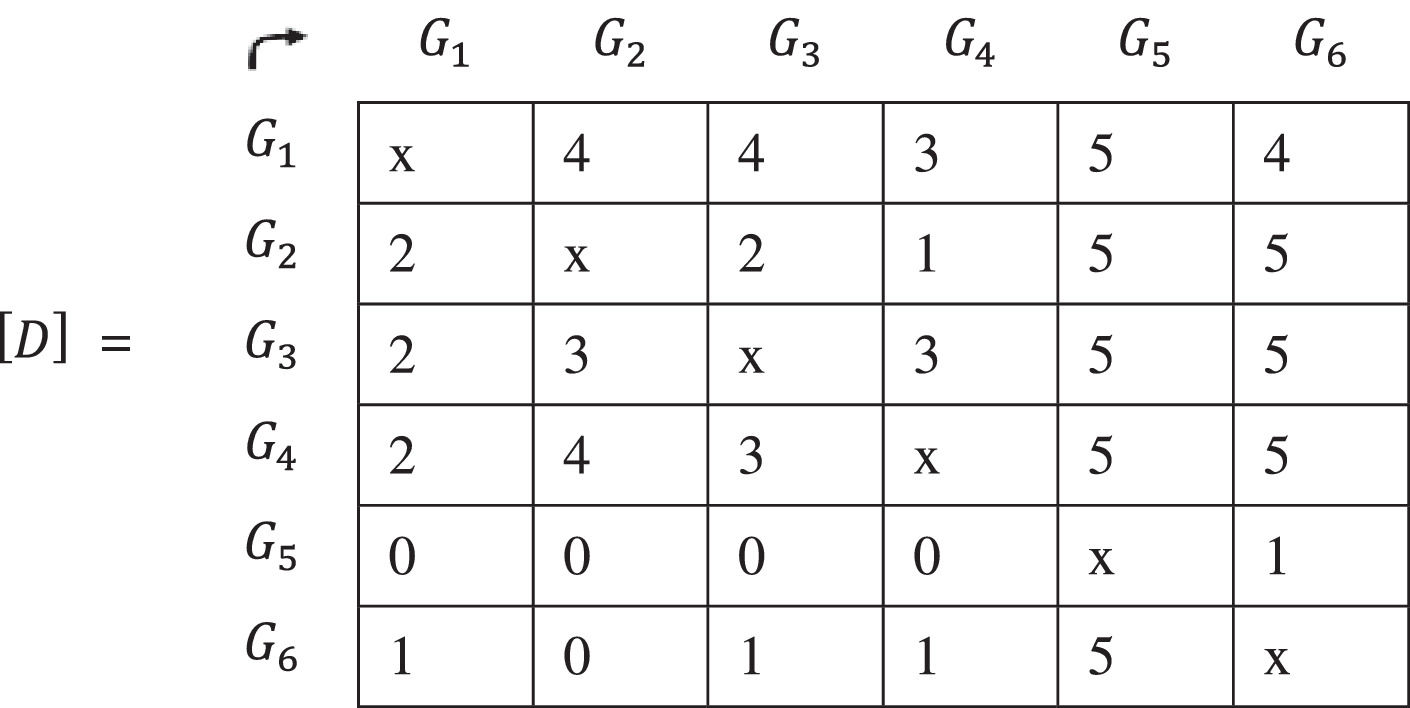
10. For each element of the matrix (G1,G2),(G1,G3)…. we add the times in which G1 has been preferred to G2, preferred to G3 and so on… that is, the value 1 of the five matrixes.
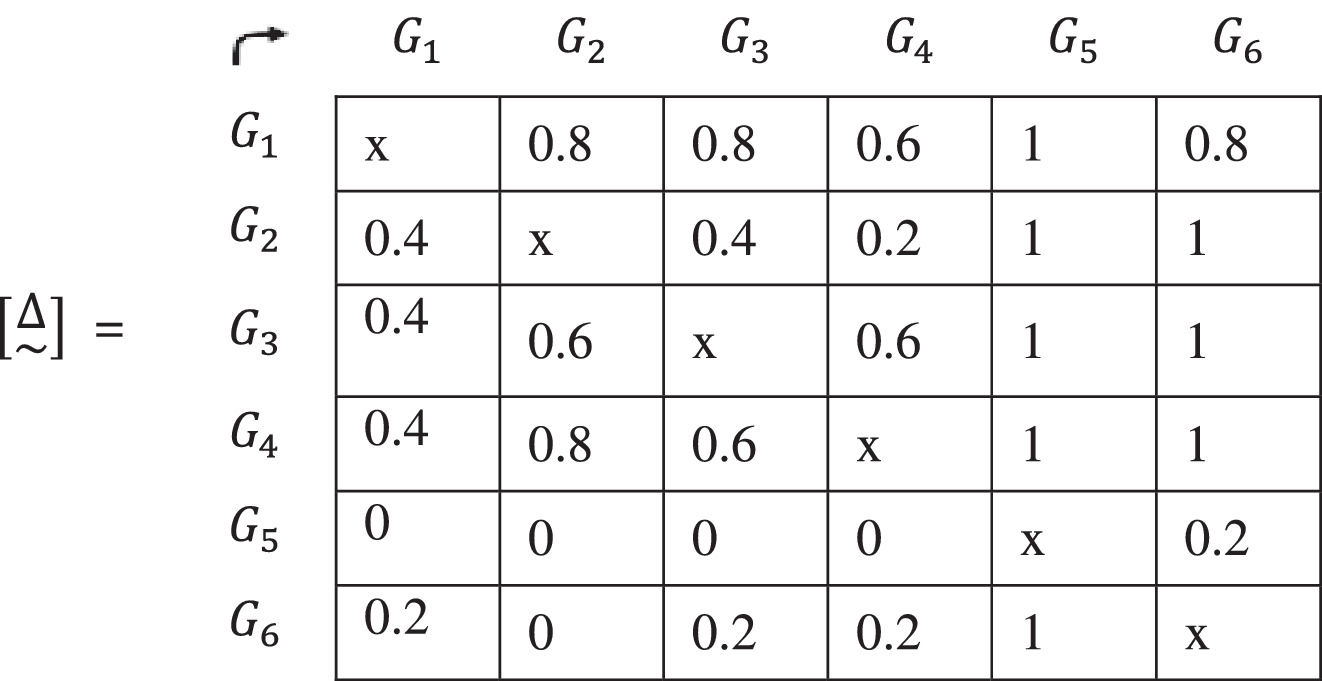
11. To continue in the hendecadary system, the value of each element of the matrix [D] is divided by the number of criteria, in this case 5. The matrix [Δ~] is found.
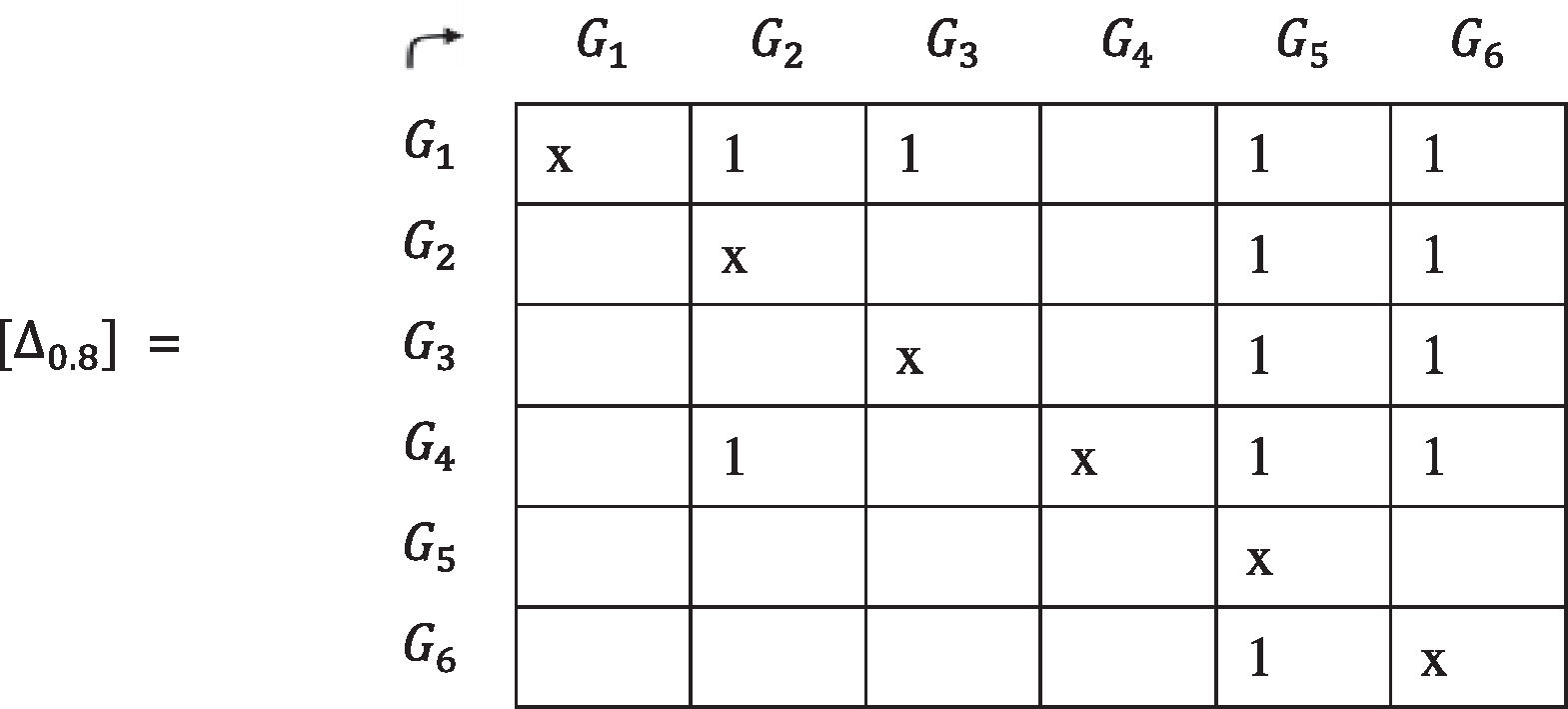
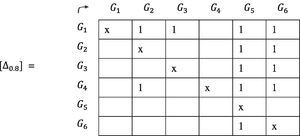
12. The matrix [Δ~] is decomposed in α-cuts. As an example, the cut α0.8 is chosen:
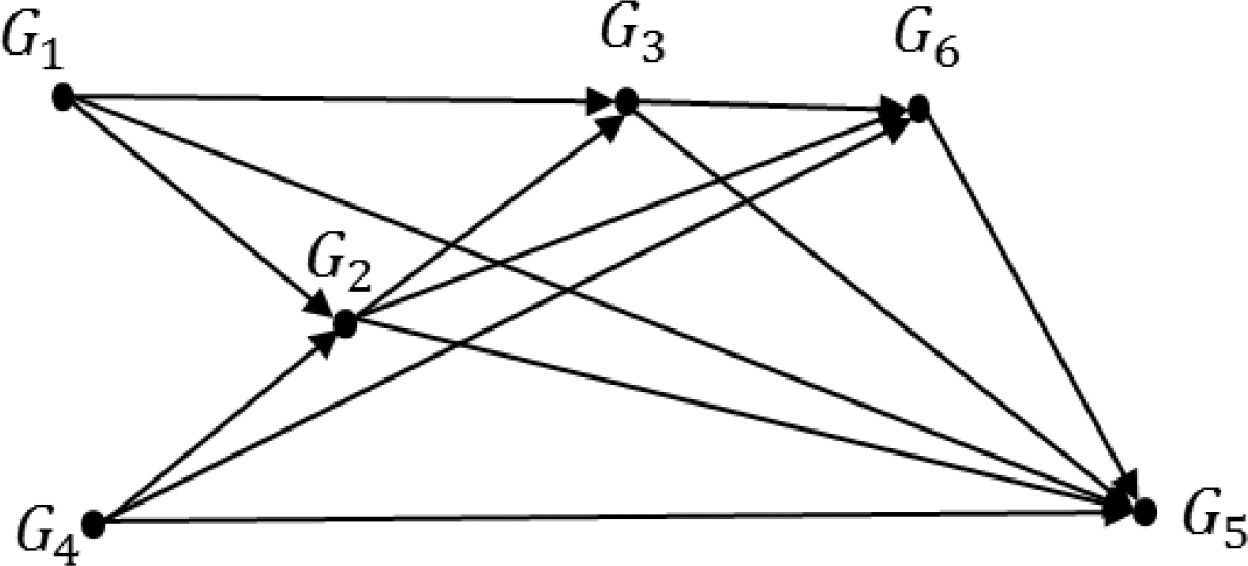
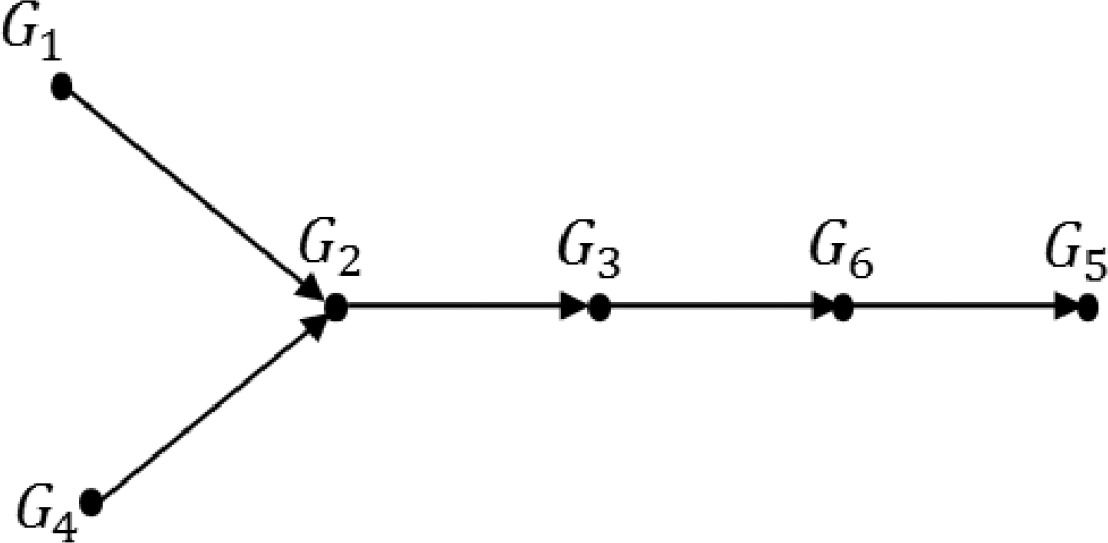
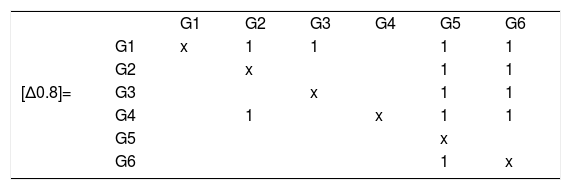
We can represent the matrix [Δ0.8] in a sagittate form as shown in Fig. 1, in this case a "partial order" that is customarily represented in a sagittate graph is drawn as in Fig. 2.
We can see that there is no order between the groups of people G1 and G4. The only thing that the graph indicates is that both precede the group G2 and all the others. This phenomenon, which can be solved by incorporating a complementary criterion, is very frequent in this type of problem management. Another important aspect to consider (which is also solvable with one or more complementary criteria) is the case of partial circuits, other times solved with the union of the affected groups. Both aspects can be approached without great practical problems.
4Discussion and conclusionsThe enormity of the alarmist stories in the mass media paint a picture of a black future due to our defenselessness in front of an unknown pandemic and its consequences to our individual lives, our economic systems, and societies. There is no denying that the ongoing waves of the SARS-Cov-2 virus with its regional mutations (Callaway, 2020) have caused unimaginable pain and death toll and confusion, closure of companies, business and institutions. The news we are receiving nowadays from, for example, India or Brazil, are indeed terrifying (Bhadra et al., 2021). What is probably more terrifying is that deaths, losses and disruption will keep on happening. However, we also want to highlight the 'silver linings', even if by doing so, we are 'risking' it to be interpreted as an act of non-conformism. The health care workers' heroism and sacrifice, supported with the technology, science, knowledge, and evolution of the societies achieved since the last deadly pandemic, has no comparison (Resnick, 2020; Spoorthy et al., 2020). On top of that, we have a 'weapon' – the vaccine, which, when distributed effectively (Mills & Salisbury, 2021), will help achieve herd immunity and will allow us to commence the 'new normal', leading to the most needed economic revival (Graham, 2020).
Sadly, the results of achieving herd immunity, at least until now, have been disappointing and, in certain cases, might even be giving an impression of guesswork. In Italy, for example, the voices have been raised in order to ‘prioritize’ vaccination for younger people, as they are those who ‘spread’ the virus the most; German physicists are proposing a solution for vaccinating the population aged 65+ in order to avoid another lockdown (Gros & Gros, 2021). In the Spanish region of Cataluña, the latest guideline is to focus on vaccinations for the Civil Guard and policeman, delaying the jabs for citizens who are over 70 years old (El Mundo, 2021).
Observing the current status of the world and how different countries manage vaccination in different ways, it is essential to note that there is not a single correct approach. And it is precisely the reason for our proposal for applying the fuzzy subset theory, as we believe it will bring order and will help governments to find the best possible solution for vaccine distribution. What is needed now more than ever is exactly what the humanist algorithms elaborated in this paper have to offer: flexibility, adaptability (and resilience), collaboration on every possible level (intergenerational, international and within interdisciplinary fields of the scientific community) and critical thinking.
The main advantage of the approach presented in this work is that it can move beyond the limitations of the existing schemes. It is taking into consideration as many criteria as needed, and not only, for example, age (Levin et al., 2020) and those of objective character, but the subjective ones, that cannot be measured by giving them a rigid value but must be accounted for (which are, in other words, not susceptible of measurement, but instead of valuation). The relative importance of different criteria is often not considered because of the heterogeneity of the components. However, thanks to the 'technic' of clustering, this common anomaly is avoided. Another advantage of the method presented is its flexibility and adaptability. Taking into consideration the complexity of the task we placed on ourselves – that of establishing a tool for effectible distribution of the vaccine order in different communities – we were faced with an 'obstacle' in the process of constructing the theoretical framework. Should we develop a single algorithm, or work on a completely new approach, in which every one of the three established problems/issues would be 'solved' with the support of the distinctive concept within the theory of the non-numerical mathematics of uncertainty? Although more challenging, we have opted for the second choice and applied the theory of clustering (because of the massive number of people to be vaccinated of different characteristics), the theory of allotment (because of the necessity to apply different kinds of vaccine adequate for different people within the clusters) and the theory of ranking, indispensable for obtaining the looked-for order of the vaccine priority for the established homogenous groups.
Again, it is crucial to note that the flexible and adaptive character of the algorithms permits, if need be, to 'group' them in one single algorithm, which will require the minimum number of adjustments. However, as any other study, ours is not free from certain limitations. We are very aware that the biggest shortcoming of the work presented is its theoretical nature and lack of empirical results. We have formulated a ‘ready-to-go’ solution for the problem of vaccine distribution in any given community, but, due to the lack of data, caused mainly by the ongoing immediacy of the vaccination programs, we were not able to apply this newly developed tool to, colloquially speaking, reality. At the same time, it is crucial to highlight that for future studies we have planned the collaboration with a multi-disciplinary team which will allow us to develop and deploy a program capable of handling and working with big data sets.
The following steps for developing this research is in the hands of the Interdisciplinary Committees around the globe. Hopefully, the ready-to-use tool we have presented will help bring a more effective, efficient and non-discriminatory fight against the spread of the COVIS-Sars-2 virus, reviving hope and more sustainability, so crucial for a much-needed global economic revival after this times of crisis. We are optimistic that the tools provided renders us much better 'prepared' for this fight than we were in times of the Spanish flu barely 100 years ago. We need to give knowledge and reason a chance, remembering that human beings are so complex and unpredictable that what we should aim for is not getting everything always right, but making sure that we are wrong as little as possible (Gil-Aluja, 2019). In the world of uncertainty, it seems that it is all we could ever ask for.






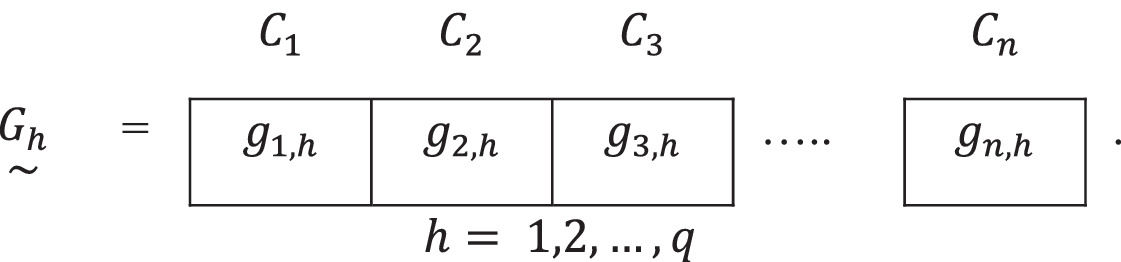
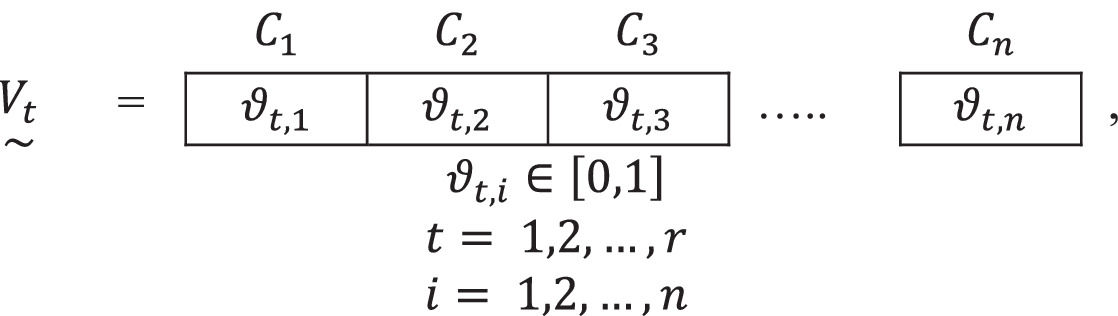


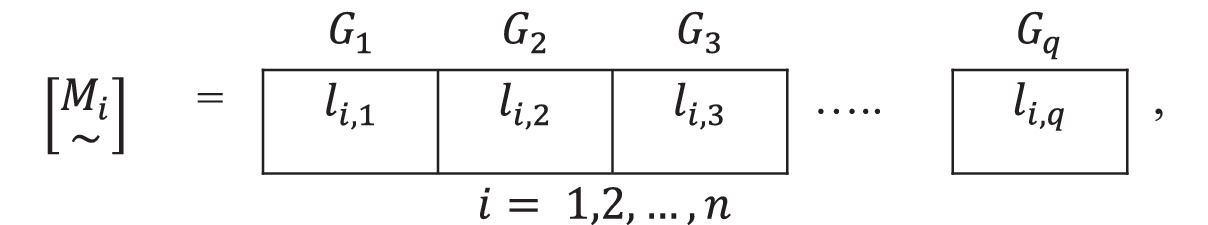


































![Representation of the matrix [Δ0.8] in a sagittate form. Representation of the matrix [Δ0.8] in a sagittate form.](https://static.elsevier.es/multimedia/24448834/0000002700000003/v1_202111140542/S2444883421000322/v1_202111140542/en/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Customary representation of the matrix [Δ0.8] in a sagittate form. Customary representation of the matrix [Δ0.8] in a sagittate form.](https://static.elsevier.es/multimedia/24448834/0000002700000003/v1_202111140542/S2444883421000322/v1_202111140542/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)

