La investigación sobre el desarrollo cognitivo indica que el ser humano posee un sentido numérico al que se viene denominando “Sistema de Aproximación Numérica” (SAN). Existen también características diferentes para el sistema de representación de números simbólicos, denominado “Sistema Numérico Preciso” (SNP). En este contexto, los objetivos del estudio han sido: (a) identificar y evaluar longitudinalmente el desarrollo de las habilidades de representación de las magnitudes simbólicas y no-simbólicas; y (b), analizar las relaciones entre dichas habilidades y la competencia matemática. El presente estudio longitudinal, se ha llevado a cabo con una muestra de 31 participantes de Educación Infantil, durante dos años, con cuatro momentos de evaluación. Los resultados sugieren que en 3° de Educación Infantil (5 años), las habilidades de procesamiento de magnitud simbólica se incrementan rápidamente hasta superar a las no-simbólicas. Por otro lado, la comparación de magnitudes simbólicas ha tenido un mayor valor de predicción sobre el rendimiento matemático en las edades evaluadas. Se discute si estas habilidades pueden ser de interés como instrumentos de detección y evaluación en el ámbito de las matemáticas, así como para intervenciones en alumnado con dificultades de aprendizaje de las matemáticas.
Research on cognitive development suggests that the human being has a number sense called “Approximate Number System” (ANS). There are also different characteristics for the representation system of symbolic numbers, called “Accuracy Number System”. In this context, the aims of the study were: (a) to identify and longitudinally evaluate the development of symbolic and non-symbolic magnitude representation skills; and (b) analyze the relationships between these skills and mathematical achievement. The present longitudinal study was carried out with a sample of 31 Early Childhood Education participants, for two years, with four evaluations timing. Results suggested that at the age of 4 years, symbolic magnitude processing abilities increased quickly until they surpass non-symbolic ones. On the other hand, the comparison of symbolic magnitudes had a higher predictive value on mathematical performance at the ages evaluated. It is discussed whether these skills may be of interest as detection and assessment tools in the field of mathematics, as well as for interventions in students with mathematics learning difficulties.
El desarrollo aritmético de los niños a menudo se ha relacionado con su “sentido numérico” (Dehaene, 2011; Devlin et al., 2022), lo que significa tener, entre otras, capacidad para manejar y representar magnitudes no-simbólicas (por ejemplo, puntos u otros objetos concretos). La investigación sobre el desarrollo cognitivo indica que poseemos un sentido numérico como es el Sistema de Aproximación Numérica (SAN) (Odic y Starr, 2018) que se considera innato. Son numerosos los estudios que sugieren que animales y humanos compartimos esta capacidad de representación de magnitudes no-simbólicas (Bryer et al., 2022), que sería congénita y universal, y cuya precisión aumenta con la edad (Dehaene, 2011). Las habilidades no-simbólicas emergen tempranamente y se desarrollan a lo largo del tiempo (Braeuning et al., 2021). Libertus et al. (2011) han evaluado habilidades no-simbólicas y han encontrado que a los 4 años son capaces de completar una tarea de comparación no-simbólica. También, Toll et al. (2015) han examinado las habilidades no-simbólicas con un rango mayor de 1 al 100 y han hallado resultados similares en escolares de 4 años. Otros estudios (Barroso et al., 2021) han explorado la comparación no-simbólica en niños/as de 5 años y mayores, encontrando que ésta mantiene un desarrollo continuo durante la infancia, llegando incluso hasta la edad adulta (Hyde et al., 2014). Durante el desarrollo infantil, las habilidades no-simbólicas se van reorganizando constantemente, hasta que al llegar a la edad adulta se puede discriminar exitosamente entre conjuntos con una ratio de 10:11 (Wang et al., 2021).
Sin embargo, el sistema de representación de números simbólicos, también denominado Sistema Numérico Preciso (SNP) posee características diferentes: (1) es un sistema adquirido que se ve afectado por el lenguaje (Xenidou-Dervou et al., 2015); (2) representa las cantidades de forma precisa (Mussolin et al., 2014); y (3) puede manipular cada vez un mayor rango de números con precisión al avanzar la edad (Praet y Desoete, 2014). La capacidad para aproximar números de manera no verbal es un factor relevante en el razonamiento cuantitativo a lo largo del desarrollo humano (Wang et al., 2021).
La investigación también ha mostrado que las habilidades simbólicas suelen aparecer a los 5 años, generalmente antes del inicio de la educación formal (Kolkman et al., 2013). Gilmore et al. (2007) argumentan que los niños pueden realizar esta tarea con la ayuda del SAN. Es plausible que conviertan los números arábigos en numerosidades no-simbólicas, mostrando una habilidad de correspondencia que permite el proceso de transformación de una representación no-simbólica a una representación simbólica (Barth et al., 2009). Se trata de una de las habilidades que deben desarrollar para lograr la comprensión de las interconexiones entre los símbolos y las cantidades que éstos representan.
La relación entre habilidades simbólicas y no-simbólicas está sujeta a debate entre los investigadores (Goffin y Ansari, 2019) y plantea diferentes preguntas de investigación todavía no resueltas (Wong et al., 2022). Se conoce que las habilidades simbólicas y no-simbólicas son diferentes (Kolkman et al., 2013) y se basarían en dos sistemas distintos que no compartirían la misma capacidad subyacente (Xenidou-Dervou et al., 2015). Matejko y Ansari (2016), han encontrado que las habilidades de procesamiento de la magnitud simbólica y no-simbólica tienen distintas trayectorias evolutivas y que el desarrollo de los dos formatos solo se relaciona entre sí en el primer año de escolaridad formal (1° de Educación Primaria-EP o Grado 1), donde las habilidades de procesamiento de magnitud simbólica afectan posteriormente a las no-simbólicas.
Otros investigadores consideran que tanto las habilidades de comparación no-simbólicas como simbólicas, en cierta medida, se basan en el SAN (Chen y Li, 2014; Van Marle et al., 2014). Además, una buena parte de los estudios se han centrado en el análisis de la relación entre habilidades de representaciones no-simbólicas y simbólicas (Gobel et al., 2014; Kolkman et al., 2013; Toll et al., 2015). Dicha correlación a veces no ha sido tan evidente (Fazio et al., 2014). Los resultados disponibles no son totalmente congruentes. Esto hace que el desarrollo de ambas trayectorias no esté explicado con claridad. Un elemento que dificulta esta clarificación es el uso de tareas de evaluación demasiado difíciles (Xenidou-Dervou et al., 2015), como las sumas aproximadas. A partir de esta discrepancia entendemos que es relevante conocer la influencia del procesamiento simbólico sobre el no-simbólico, en una franja evolutiva (4 a 7 años), sobre los que hay menos resultados concluyentes.
La asociación entre la representación no-simbólica y la capacidad matemática tiene todavía un margen amplio para la investigación, pues no está completamente resuelta. Diferentes estudios han encontrado correlaciones positivas entre las habilidades de representación no-simbólica y la capacidad matemática en niños y adultos (Chen y Li, 2014; Schneider et al., 2017). Sin embargo, otros no han encontrado correlación entre la precisión del SAN y las matemáticas (Nosworthy et at., 2013; Lyons et al., 2014; Sasanguie et al., 2014). No obstante, los investigadores han llegado a un cierto consenso al considerar que las habilidades simbólicas tienen un impacto significativo en la capacidad matemática. En esta línea, Bugden y Ansari (2011) han encontrado esta correlación significativa en alumnado de 1° y 2° de EP. Asimismo, Toll et al. (2015) han informado que las habilidades de comparación simbólica son el predictor más importante de la capacidad matemática. Del mismo modo, Van Marle et al. (2014) han investigado las habilidades simbólicas como un mediador potencial de la relación entre el procesamiento de magnitud no-simbólica en alumnado de 3 a 4 años y matemáticas al final del primer curso de EI. Refieren un modelo de mediación múltiple que predice la relación entre el SAN y la competencia matemática, mediado por el SNP. También se han encontrado similares resultados en escolares de 6 años (Gobel et al., 2014). Por último, Scalise y Ramani (2021) han llevado a cabo un estudio longitudinal con alumnado de 3 a 5 años, encontrando que las habilidades de comparación simbólica se relacionan con el desarrollo de la comprensión posterior de la cardinalidad, las habilidades de suma y de resolución de problemas. Hay que tener en cuenta que, además, el contexto de desarrollo tiene una significativa incidencia sobre las posibilidades de éxito, dado que la estimulación cognitiva y el apoyo emocional son también variables críticas en el ajuste del rendimiento académico (Heckman, 2011).
En este contexto, el presente estudio plantea dos objetivos: (1) identificar las trayectorias del desarrollo de las habilidades de representación de magnitudes no-simbólica y simbólica, evaluadas con tareas de comparación de magnitudes La evidencia disponible muestra discrepancias sobre las conexiones entre ambas habilidades de comparación; y (2) analizar la relación y la mediación entre habilidades de representación de magnitudes simbólicas-no-simbólicas, y la capacidad matemática en Educación Infantil (EI) de 4-5 años y el inicio del 2° curso de la EP (6 a 7 años). Como se ha sugerido, diversos estudios se han centrado en diferentes rangos de edad, distintas cantidades dentro y fuera del rango de subitización, generándose resultados diversos y no coincidentes (Hutchison et al., 2020). Esta investigación se centra en un rango de 4 a 7 años y la predicción es que las relaciones entre estos tres tipos de habilidades (comparación simbólica, no-simbólica y rendimiento en matemáticas), sean diferentes en función de la edad y la variación de la escolarización de los participantes a lo largo del tiempo.
MétodoParticipantesCuarenta y siete estudiantes con desarrollo evolutivo típico, de 3° de EI han sido seleccionados de manera incidental, para participar en un estudio longitudinal sobre el desarrollo de habilidades matemáticas, con cuatro momentos de evaluación. Por diferentes razones, esta muestra inicial ha quedado constituida finalmente por un total de 31 participantes. Los 16 casos perdidos lo han sido por cambio de centro escolar, renuncia al consentimiento informado, o por razones desconocidas para los investigadores. Este alumnado está compuesto por 20 niñas y 11 niños con un promedio de edad de 5.2 años [DT=3.32 años; rango de 4(9) a 5(9)] en la primera sesión de evaluación. Los participantes son alumnos de un centro escolar concertado de clase media, con acceso gratuito de una ciudad de 130.000 habitantes.
InstrumentosComparación de magnitudes simbólicas y no-simbólicas (Nosworthy et al., 2013). Examina las habilidades de procesamiento de magnitudes de carácter simbólico, con 56 pares de dígitos arábigos (entre 1 y 9) y comparación no-simbólica mediante 56 pares de puntos en un cuadernillo impreso. La relación (pequeño/grande) entre los pares de números y conjuntos de puntos han oscilado entre .11 y .89 (por ejemplo, la relación entre 3 y 5 sería .60). Se presentan antes los estímulos con proporciones relativamente más pequeñas que los de proporciones mayores. Los participantes, en un tiempo de dos minutos por cada tipo de comparación, deben marcar con un lápiz el elemento del par que es mayor o en el cual hay más. El valor del coeficiente Omega de McDonald para la subprueba de comparación simbólica ha sido .735, y para la no-simbólica .722.
Test de Competencia Matemática Básica (TEMA-3; Ginsburg y Baroody, 2003). Esta batería, evalúa conceptos y habilidades formales e informales en diferentes campos: conteo, comparación de números, lectura de los números y los signos, dominio de los hechos numéricos, habilidades de cálculo y comprensión de conceptos. Se compone de 72 ítems y ha obtenido un coeficiente Omega de McDonald de .853.
ProcedimientoLos participantes han sido individualmente evaluados en un contexto escolar apropiado para la realización de este tipo de pruebas, situados en una habitación tranquila del centro durante el horario escolar, respetando los tiempos de descanso. Las evaluaciones han sido realizadas por los autores y autoras, con experiencia en la evaluación con este tipo de pruebas. Cada evaluación individualizada se ha realizado en dos sesiones, de unos 45 minutos de duración máxima aproximadamente, siguiendo las instrucciones del manual de administración de las pruebas correspondientes. La secuencia temporal de evaluación del estudio longitudinal, así como las pruebas administradas en cada momento, se especifica en la Tabla 1.
Línea de tiempo de la evaluación del estudio longitudinal, con las pruebas administradas en cada momento (T)
| Tareas administradas | Educación Infantil(5 años)(1er trimestre)T1Inicio curso | Educación Infantil(5 años)(3er trimestre)T2Final curso | Educación Primaria (1°)(6 años)(1er trimestre)T3Inicio curso | Educación Primaria (2°)(7 años)(1er trimestre)T4Inicio curso |
|---|---|---|---|---|
| Comparación de magnitudes simbólicas y no-simbólicas | X | X | X | X |
| Test de Competencia Matemática Básica (TEMA-3) | X | X | X |
Antes del inicio del estudio, se ha obtenido el consentimiento informado por escrito de las familias de los participantes, así como del centro escolar. Se han seguido los protocolos legales de garantías éticas para el desarrollo del estudio, tanto en relación a las autorizaciones como a la protección de los datos. Este trabajo ha seguido el Código Ético Internacional en Humanidades y Ciencias Sociales del Centre for Research Ethics and Bioethics.
Análisis de datosEn primer lugar, se han llevado a cabo análisis descriptivos para examinar las tendencias de los datos y su distribución, con la finalidad de detallar los resultados de la muestra que ha formado parte del estudio. Del mismo modo, se ha realizado un análisis inferencial utilizando la ANOVA con medidas repetidas, atendiendo la administración de las mismas pruebas en distintos momentos del desarrollo, y pruebas post hoc de Bonferroni para evaluar las diferencias entre las medias específicas. Los datos cumplen la condición de esfericidad (W de Mauchly), ya que la probabilidad asociada es mayor a p>.05 (W=917, p=.33). Asimismo, se han calculado las correlaciones para estudiar la asociación entre dos variables numéricas y su tendencia creciente o decreciente. Para estudiar el peso predictivo de la comparación simbólica y no-simbólica en los distintos tiempos sobre la competencia matemática, se han realizado análisis de regresión lineal, arrojando luz acerca del porcentaje de variabilidad en la competencia matemática temprana tomando como variables predictoras las destrezas de comparación de magnitudes. Finalmente, se ha llevado a cabo un análisis mediacional simple con PROCESS (3.4.1), basándonos en la estrategia de pasos causales (Baron y Kenny, 1986) y que se ha sustentado sobre el análisis de regresión, con la finalidad de establecer un posible modelo explicativo causal de la relación entre el SAN y la competencia matemática, y sus variables mediadoras.
ResultadosDesarrollo de habilidades de procesamiento de magnitud simbólica y no-simbólicaEl alumnado ha sido altamente preciso tanto en la comparación simbólica como en la no-simbólica, lo que puede sugerir una buena comprensión de las instrucciones. Los análisis estadísticos adicionales se han realizado con las puntuaciones del número total de ítems acertados. La Tabla 2 recoge los valores estadísticos calculados para las variables de estudio en los cuatros tiempos de evaluación.
Media, desviación típica y rango calculados para las variables del estudio longitudinal. Tiempos de evaluación T1, T2, T3 y T4
| Comparación simbólica | Comparación no-simbólica | TEMA-3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | T1 | T2 | T4 | |
| Media | 31.29 | 39.51 | 44.45 | 51.74 | 35.35 | 39.38 | 43.80 | 47.64 | 18.45 | 25.87 | 48.03 |
| DT | 10.40 | 7.99 | 9.18 | 5.34 | 6.56 | 6.37 | 6.14 | 6.21 | 4.22 | 5.85 | 8.23 |
| Rango | 9-55 | 15-51 | 18-56 | 40-56 | 25-47 | 25-47 | 27-54 | 36-56 | 9-28 | 13-42 | 32-67 |
Para examinar cómo las habilidades de procesamiento de magnitud simbólica y no-simbólica cambian durante el período de tiempo entre tercero de EI (edades de 4 a 5 años) y el inicio de segundo de EP (edades de 6 a 7 años), se ha llevado a cabo un ANOVA de medidas repetidas con el tipo de tarea (simbólica versus no-simbólica) y el tiempo de evaluación (T1, T2, T3 y T4) como factores de comparación. Este análisis ha revelado que no se da un efecto principal del tipo de tarea: F(1, 30)=.053, p=.819, η2=.002. Pero sí un efecto principal de la variable tiempo de evaluación: F(3, 90)=56.19, p<.0001, η2=.65, aumentando los aciertos con el tiempo transcurrido. Asimismo, ha habido un efecto de interacción tarea x tiempo: F(3, 28)=11.48, p<.0001, η2=.27. Los participantes se desempeñan mejor en la tarea no-simbólica (M=35.35, DT=6.56) que en la simbólica (M=31.29, DT=10.4) en el T1; el desempeño en la comparación simbólica mejora a lo largo del estudio longitudinal más que la no-simbólica (MT1=31.29,MT2=39.51,MT3=44.45;MT4=51,74). Se han realizado pruebas Bonferroni post hoc corregidas para examinar las características cuantitativas de la interacción tarea x tiempo. Los participantes han mostrado mejores resultados en la tarea no-simbólica en el T1 (p<.0001). En los T2 y T3 las diferencias no han sido significativas (p=.33). Los datos sugieren que el rendimiento no simbólico es superior al rendimiento simbólico en la primera evaluación (T1) (alumnado de EI de 4 años). Posteriormente (evaluación T4), vuelve a haber diferencias estadísticamente significativas en el inicio del 2° curso de EP (7 años), cuando claramente los resultados en la tarea simbólica han sido superiores a la no-simbólica (p<.0001).
Por otro lado, los resultados de las correlaciones (Tabla 3), indican que el rendimiento simbólico y no simbólico correlaciona significativamente en el T1 (r(31)=.57, p<.001), T2 (r(31)=.68, p<.001), T3 (r(31)=.60; p<.0001) y T4 (r(31)=.65, p<.0001).
Correlaciones de Pearson calculadas entre las diferentes pruebas administradas en el estudio longitudinal
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. CS1 | 1 | .577** | .500** | .314 | .352 | .324 | .296 | .130 | .331 | .303 | .406* |
| 2. CNS1 | 1 | .183 | .183 | −.093 | .079 | .014 | .061 | .265 | .239 | .315 | |
| 3. CS2 | 1 | .685** | .608** | .420* | .680** | .366* | .422* | .392* | .482** | ||
| 4. CNS2 | 1 | .378* | .521** | .497** | .515** | .328 | .295 | .426* | |||
| 5. CS3 | 1 | .604** | .590** | .352 | .108 | .240 | .257 | ||||
| 6. CNS3 | 1 | .264 | .229 | .290 | .327 | .459** | |||||
| 7. CS4 | 1 | .654** | .340 | .387* | .505** | ||||||
| 8. CNS4 | 1 | .330 | .356* | .326 | |||||||
| 9. TEMA-3 T1 | 1 | .819** | .717** | ||||||||
| 10. TEMA-3 T2 | 1 | .708** | |||||||||
| 11. TEMA-3 T4 | 1 |
*p<.05. **p<.01
Para indagar la naturaleza de la relación entre rendimiento simbólico y no simbólico en los momentos de evaluación, se han llevado a cabo diversas regresiones para determinar si el rendimiento simbólico y no simbólico de los T1, T2 y T3 predice puntuaciones de los T2, T3 y T4 respectivamente (Tabla 4).
Resultados del análisis de regresión lineal (1.a y 1.b) que predice la destreza de comparación simbólica a partir de las puntuaciones en las pruebas de comparación simbólica y no-simbólica como variables predictoras en los Tiempos 1, 2, 3 y 4
| Tiempo 2 | Tiempo 3 | Tiempo 4 | ||||
|---|---|---|---|---|---|---|
| β | t | β | t | β | t | |
| Comparación Simbólica | .591** | 2.980 | .658** | 3.201 | .678** | 3.575 |
| Comparación No-simbólica | −.158 | −.797 | −.073 | −.356 | −.145 | −.766 |
**p<.001
La primera regresión lineal (1.a) que usa la puntuación simbólica del Tiempo 2 como variable dependiente (y como variable predictora la comparación simbólica y no-simbólica del T1), es estadísticamente significativa: F(2, 30)=5.09, p<.013. En este modelo, sólo las puntuaciones simbólicas del T1, predicen una varianza única en las puntuaciones simbólicas del T2 (la comparación no-simbólica no ha tenido valor predictivo).
La segunda regresión lineal (1.b.) en la que se ha utilizado la puntuación simbólica del T3 como variable dependiente y las puntuaciones simbólicas y no-simbólicas del T2 como variables predictoras, ha sido significativa: F(2, 30)=8.308, p<.001. Aquí sólo las puntuaciones simbólicas del T2 (pero no las no-simbólicas T2), predicen una varianza única en las puntuaciones simbólicas del T3.
Por último, la regresión lineal que utiliza la puntuación simbólica del Tiempo 4 como variable dependiente y las puntuaciones simbólicas y no-simbólicas del T3 como variables predictoras ha sido significativa: F(2, 30)=7.919, p<.002. Solo las puntuaciones simbólicas del T3 predicen una varianza única en las puntuaciones simbólicas del T4. Nuevamente, la puntuación no-simbólica no ha tenido valor predictivo sobre la simbólica. Se ha realizado otra serie de análisis de regresión lineal (2.a) con las puntuaciones no-simbólicas de T2, T3 y T4 como variable dependiente y las puntuaciones simbólicas y no-simbólicas de los T1, T2 y T3 como predictoras (Tabla 5).
Resultados del análisis de regresión lineal (2.a, 2.b y 2.c) que predice la destreza de comparación no-simbólica a partir de las puntuaciones en las pruebas de comparación simbólica y no-simbólica como variables predictoras en los Tiempos 1, 2, 3 y 4
| Tiempo 2 | Tiempo 3 | Tiempo 4 | ||||
|---|---|---|---|---|---|---|
| β | t | β | t | β | t | |
| Comparación Simbólica | .311 | 1.418 | .119 | .539 | .337 | 1.51 |
| Comparación No-simbólica | −.004 | .017 | .439** | .199 | .026 | .117 |
**p<.001
La predicción que se había hecho con la puntuación simbólica y no-simbólica del T1 sobre la puntuación no-simbólica del T2, no ha sido significativa: F(2, 30)=1.527, p=.235 y los puntajes simbólicos y no simbólicos en el T1 no han predicho una varianza única. En la segunda regresión lineal (2.b.) hemos usado la puntuación no-simbólica del T3 como variable dependiente y las puntuaciones simbólicas y no-simbólicas del T2 como variables predictoras, resultando que es significativa; F(2, 30)=5.403, p<.01. Sólo las puntuaciones no-simbólicas del T2, predicen una varianza única en las puntuaciones no-simbólicas del T3.
En la última regresión lineal calculada (2.c.) hemos usado la puntuación no-simbólica del T4 como variable dependiente y las puntuaciones simbólicas y no-simbólicas del T3 como variables predictoras; no han sido significativas: F(2, 30)=1.99, p=.056. Ni las puntuaciones simbólicas ni las no-simbólicas del T3 predicen una varianza única en las puntuaciones no-simbólicas del T4.
Procesamiento de magnitud simbólica y no-simbólica y resultados matemáticosEn la Tabla 2 se han mostrado las medias obtenidas por los participantes en el TEMA-3 en tres momentos del estudio (T1), (T2) y (T4). En la última evaluación, el alumnado (6 a 7 años de edad) ya ha completado el primer curso de EP y está iniciando segundo. Las medias señalan un avance importante en el desarrollo de las competencias matemáticas (MT1 = 18.45,MT2 = 25.87, y MT4 = 48.03), a la vez que una mayor desviación típica y un aumento de las diferencias en competencia matemática conforme se avanza en la escolaridad. Las diferencias son significativas entre el T1 y T2: t(31)=−12.13, p<.0001 y también entre T2 y T4: t(31)=−21.22, p<.0001. Estas diferencias sugieren una mejora en las competencias matemáticas entre el último curso de EI y el inicio del segundo curso de EP.
Posteriormente, se han realizado análisis de regresión en los momentos (T1, T2 y T4) para calcular la contribución única de los dos tipos de procesamiento de magnitudes a los resultados matemáticos del TEMA-3. La Tabla 6 muestra los coeficientes beta estandarizados y los niveles de significación de los modelos de regresión en cada tiempo o momento de la evaluación del rendimiento matemático. En el T1 (al iniciar tercero de EI) los dos componentes del procesamiento de magnitudes explican una variación del 15%. Sin embargo, ni la comparación simbólica ni la no-simbólica han tenido un efecto significativo sobre el rendimiento en TEMA-3. Igual ocurre en el T2 en el que el porcentaje de variación es del 16%, sin ningún efecto significativo del procesamiento de magnitudes. En el T4, el procesamiento de magnitudes explica el 25% de la variación en el TEMA-3, pero solo la comparación simbólica tiene un efecto significativo: F(2, 30)=4.79, p<.016. El efecto predictivo de la comparación no-simbólica no ha sido significativo en ninguno de los análisis de regresión realizados.
Resultados del análisis de regresión de la comparación simbólica y no-simbólica en los resultados del TEMA-3 en los distintos momentos de la evaluación
| Tiempo 1 | Tiempo 2 | Tiempo 4 | ||||
|---|---|---|---|---|---|---|
| β | t | β | t | β | t | |
| Comparación Simbólica | .268 | 1.23 | .358 | 1.49 | .510* | 2.366 |
| Comparación No-simbólica | .110 | .507 | .049 | .207 | −.008 | −.036 |
*p<.01
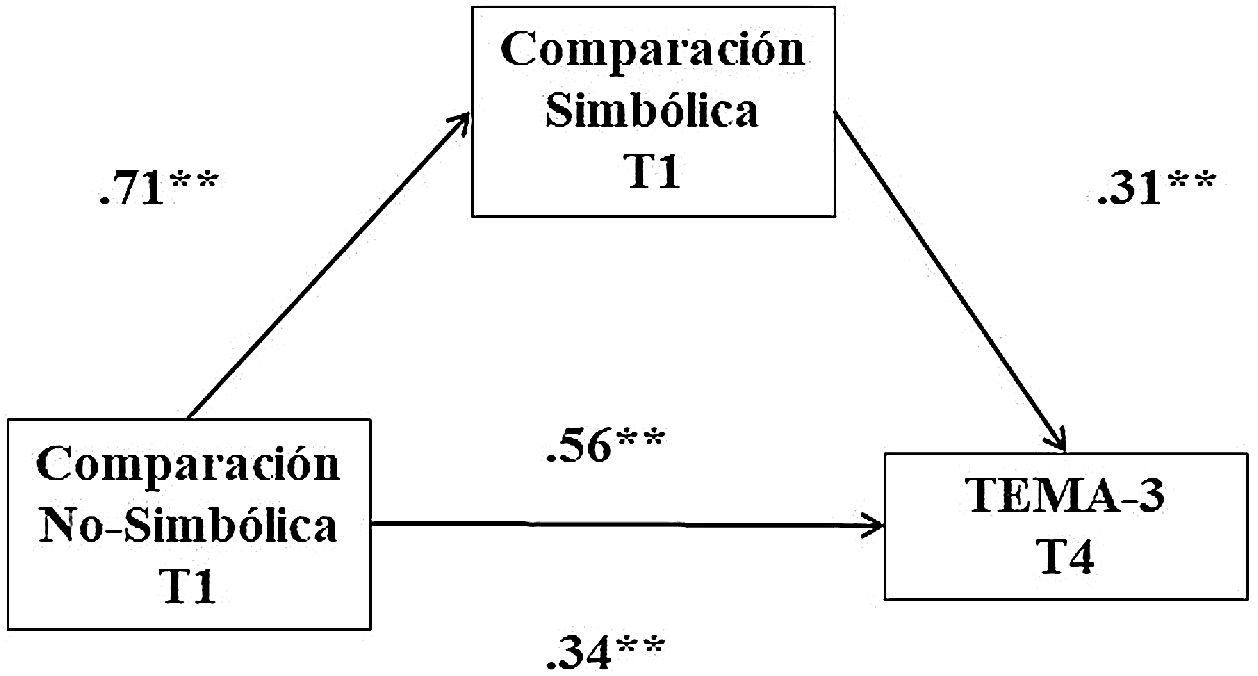
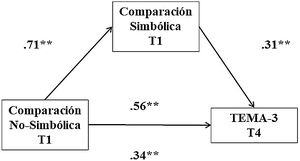
El análisis mediacional realizado para conocer la participación del componente simbólico sobre el rendimiento matemático, ha arrojado un modelo de mediación donde la comparación no-simbólica en T1 predice el rendimiento matemático en T4, mediada por la comparación simbólica (Figura 1).
En último lugar, con respecto al análisis de los efectos indirectos de la comparación no-simbólica (VI) sobre la competencia matemática (VD), considerando el papel mediador de la comparación simbólica, se han obtenido los siguientes resultados: β=.18, DT=.08, 95% IC=.04-.38. Considerando el intervalo de confianza, observamos que el efecto de la variable mediadora es estadísticamente significativo. En conclusión, la habilidad en comparación no-simbólica en el T1ha tenido un efecto en la competencia matemática temprana en el T4, que está mediado por las destrezas en comparación simbólica en el T1. Del mismo modo, se han incluído los resultados derivados del cálculo del modelo inverso, en el que la comparación no simbólica se determina como variable mediadora. El resultado ha sido el siguiente: β=.15, DT=.07; 95% IC=.001-.292. A la luz de los resultados, el efecto de la comparación no simbólica en T1 como variable mediadora en la predicción de la comparación simbólica en T4 es significativa, pero con valores muy cercanos a cero en el intervalo de confianza, deja de serlo en T2 (β=.14, DT=.08, 95% IC=−.009-.325). Este patrón también se ha repetido en T4 (β=.11, DT=.07, 95% IC=−.03-.27).
DiscusiónUn primer objetivo de este estudio ha sido identificar las trayectorias del desarrollo de las habilidades de representación de magnitudes no-simbólica y simbólica, evaluadas con tareas de comparación de magnitudes. No son abundantes los estudios longitudinales en el estudio de estas trayectorias. El trabajo de Matejko y Ansari (2016) se limita a un seguimiento de un curso escolar, al inicio de la educación formal: los participantes a los 5 años rinden mejor en la tarea no-simbólica que en la simbólica. Sin embargo, a medida que aprenden matemáticas más formalmente, la ventaja de las habilidades no-simbólicas desaparecen. Nuestros resultados van en esta dirección. En cada momento de la evaluación, la variable predictora (comparación simbólica) tiene más peso que la comparación no-simbólica. A medida que aprenden más sobre el sistema de representación simbólica, la ventaja del alumnado en la habilidad no-simbólica parece tener menos influencia.
El primer curso de escolarización formal es un período importante para el desarrollo de habilidades de procesamiento simbólico (Nosworthy et al., 2013). Crecen rápidamente para coincidir y superar a las habilidades de procesamiento no-simbólico. Los datos presentes replican estos hallazgos y, además, muestran que las habilidades de procesamiento simbólico tienen una trayectoria de desarrollo distinta de las no-simbólicas en la transición de EI a EP, donde las habilidades simbólicas mejoran a un ritmo más rápido (Malone et al., 2021).
En el contexto escolar del presente estudio, al iniciar el 2° curso de EP (7 años), tras un curso de enseñanza formal, los resultados sugieren que las trayectorias de desarrollo para las habilidades simbólicas y no-simbólicas son divergentes y puede continuar en el futuro. Esto indica que el desarrollo de las trayectorias puede mantenerse diferentes entre sí hasta la edad adulta (Lyons et al., 2012). Responder a la cuestión de cómo aprenden los niños el significado de los números simbólicos sigue siendo una pregunta sin respuesta. Nuestros resultados muestran que las habilidades simbólicas y no-simbólicas no están tan estrechamente vinculadas como podría esperarse durante un período en que el alumnado desarrolla rápidamente la fluidez con los números simbólicos. Si los formatos simbólicos y no simbólicos tuvieran la misma representación subyacente a lo largo del primer curso e inicios del segundo, los cambios en un sistema conducirían a cambios en el otro. Sin embargo, no se encuentra tal relación durante todo el rango de tiempo estudiado (dos años). Por otra parte, los cambios del rendimiento en el desempeño no-simbólico no siempre están relacionados con los cambios en el desempeño simbólico en los distintos tiempos de evaluación, llegando un momento en que son independientes uno de otro. Pero antes de que esto ocurra, nuestro análisis de mediación sugiere que el procesamiento simbólico contribuye al poder explicativo del procesamiento no-simbólico sobre el rendimiento matemático.
Sin embargo, no todas las evidencias disponibles apuntan a estas diferentes trayectorias de desarrollo del procesamiento de magnitud simbólica y no-simbólica. En el estudio sobre las habilidades de procesamiento de magnitud desde EI hasta el primer curso de EP, Toll et al. (2015) encuentran una moderada relación entre el crecimiento de habilidades simbólicas y no-simbólicas, lo que sugiere que los dos formatos se influyen mutuamente. Los resultados, además, revelan que la comparación simbólica es el predictor más significativo de la estimación en la línea numérica y logros matemáticos básicos. Sin embargo, en nuestro análisis de mediación inversa no se destaca la mediación del procesamiento no-simbólico sobre el simbólico. Coincidiendo con Matejko y Ansari (2016), una explicación para los resultados contrapuestos pudiera ser las diferencias entre tareas. En la tarea de comparación de magnitudes en nuestro estudio se han utilizado dígitos del 1 al 9, mientras que Toll et al. (2015) utilizaron dígitos que van desde 0 hasta 100. En el presente trabajo no se conoce una relación estadísticamente significativa, entre el desarrollo de trayectorias de los dos formatos simbólicos y no simbólicos, excepto en T4. Esto probablemente nos indica que la velocidad en el cambio de las habilidades de procesamiento simbólico y no-simbólico es diferente a lo largo del tiempo, sobre todo cuando ya se ha iniciado la educación formal.
El segundo objetivo de este estudio ha sido averiguar las asociaciones, por un lado, entre habilidades de representación de magnitudes simbólicas y no-simbólicas y, por otro, su influencia sobre el rendimiento matemático. Encontramos un efecto significativo de las habilidades simbólicas sobre el rendimiento matemático, pero no de las no-simbólicas. La literatura contrastada presenta también resultados discordantes, sobre todo en relación con la comparación no-simbólica. Fazio et al. (2014) exponen tres hipótesis sobre la relación entre capacidades no-simbólicas, simbólicas y habilidad matemática. Consideran que las habilidades no-simbólicas pueden tener efectos directos, indirectos o bien, afectar de forma independiente al rendimiento matemático. Nuestros resultados sugieren que puede existir una influencia de las habilidades no-simbólicas en habilidades matemáticas, a través de las habilidades simbólicas (ver análisis mediacional). Pero es escasa la aportación directa del procesamiento no-simbólico, por lo que parece más plausible la tercera hipótesis de Fazio et al. (2014). Estos resultados coinciden con los encontrados por Van Marle et al. (2014), que han hallado que la relación entre habilidades no-simbólicas y el rendimiento matemático está mediada por las habilidades simbólicas, de acuerdo con el modelo mediacional encontrado en nuestro estudio. En general, los resultados obtenidos muestran que el procesamiento simbólico tiene un impacto importante sobre el rendimiento matemático en el rango de edad estudiado. Esto coincide con los resultados encontrados por Li et al. (2018) para las edades de 5-7 años. No así para los de 8 años, edad en la que el impacto del procesamiento simbólico deja de ser significativo para el rendimiento matemático evaluado con el TEMA-3. En cambio, Schneider et al. (2017) indican que el procesamiento de magnitudes se asocia con la competencia matemática a lo largo de la vida en una amplia gama de tareas matemáticas. La asociación es más fuerte para el procesamiento de magnitudes numéricas simbólicas que para las no-simbólicas, como muestran también nuestros resultados. Además, el procesamiento de números simbólicos es un predictor consistente y significativo de los puntajes de rendimiento aritmético, mientras que su eficiencia de procesamiento de números no-simbólicos no lo es (Bartelet et al., 2014).
Por último, los resultados de Xenidou-Dervou et al. (2017) han mostrado que la comparación simbólica y no-simbólica tiene diferentes trayectorias de desarrollo: mejora más la simbólica que la no-simbólica. Ambas habilidades son predictores longitudinales del rendimiento matemático futuro del alumnado, más que variables como el cociente intelectual y la memoria de trabajo. La comparación no-simbólica parece ser moderadamente predictiva solo en el nivel educativo de EI. Sin embargo, la comparación simbólica predice bien el rendimiento matemático durante los tres años del estudio longitudinal.
Limitaciones y futuras líneas de investigaciónUna primera limitación de este estudio es el tamaño de la muestra, que exige que los resultados se tomen con cautela para evitar falsas extrapolaciones. Asimismo, las tareas de evaluación de la comparación de magnitudes simbólicas y no simbólicas realizadas con un test de lápiz y papel tienen ciertas limitaciones, por cuanto pueden verse afectadas por diferencias en la coordinación viso-manual de los participantes. Estos pueden presentar variaciones importantes en el rango de edad evaluado. No obstante, es importante tener en cuenta que el Numeracy Screener de Nosworthy et al. (2013) utilizado en el estudio actual, ha producido resultados comparables en múltiples estudios en diferentes contextos culturales y grupos de edad (Lau et al., 2021). Finalmente, hay que considerar que el contexto de desarrollo, las características cognitivas, emocionales y socio-demográficas son también relevantes en el análisis del rendimiento matemático (Heckman, 2011). En este continuo, una línea futura de investigación en el estudio de las trayectorias de desarrollo de magnitudes simbólicas y no simbólicas debería indagar sobre existencia o no una relación bidireccional entre los formatos de comparación dentro de diferentes rangos de subitización o mayores (Goffin y Ansari, 2019).
ConclusionesLos hallazgos del presente estudio dan cuenta de la importancia del procesamiento simbólico como variable predictora del rendimiento matemático a temprana edad y pueden tener implicaciones significativas para la evaluación y la práctica educativa. Nuestros resultados sugieren que las habilidades de comparación de magnitudes simbólicas podrían usarse potencialmente para identificar precozmente al alumnado con dificultades en matemáticas. Asimismo, en el futuro, la investigación podría analizar de manera más profunda y experimental si se consigue una mejora en el rendimiento matemático tras la aplicación de programas de entrenamiento en comparación de magnitud simbólica del alumnado de educación formal. El hecho potencial de que las habilidades de procesamiento simbólico quizás se vean afectadas por el desarrollo evolutivo y la educación, sugiere que la mejora de estas habilidades podría influir en el rendimiento matemático general en años posteriores de escolarización.
AgradecimientosEste trabajo ha recibido financiación del Ministerio de Ciencia, Innovación y Universidades (FEDER) de España. Referencia PID2019-105584GB-I00 y PID2020-119561RB-I00.