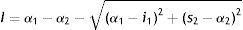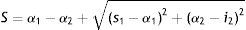El coeficiente α es uno de los métodos más utilizados para estimar la fiabilidad de las puntuaciones, pero es probable que al interior de un estudio 2 o más grupos difieran en cuanto a la magnitud de α, lo cual deviene en un problema para el investigador, ya que si en 2 grupos la estimación del error de medición es diferente, las comparaciones podrían estar sesgadas o al menos distorsionadas. Esta situación es frecuente en investigación educativa, ya que normalmente las muestras son integradas por personas de diferente sexo, carreras, ciclos de estudios, e inclusive de distintos lugares de procedencia.
Una aproximación reciente sugiere el uso de los intervalo de confianza (IC) de la diferencia entre 2 parámetros1, en este caso la diferencia de α entre grupos independientes (α1–α2). De este modo, Bonnet2 planteó una fórmula para calcular el IC de la diferencia entre 2 coeficientes α:
Donde I y S son los límites inferior y superior del IC de la diferencia entre coeficientes α (α1–α2; si se cumple α1>α2). Asimismo, α1 y α2 son los coeficientes del primer y segundo grupo; i1 y s1 son los límites inferior y superior del IC de α1; del mismo modo, i2 y s2 son los límites inferior y superior del IC de α2.
Para ejemplificar el método fue analizada la base de datos utilizada en la validación de la Escala breve de satisfacción con los estudios (EBSE)3, a fin de calcular el coeficiente α de varones y mujeres, por ser el sexo una potencial fuente de sesgo. Fue obtenida una magnitud de 0,792 (IC 95%: 0,723-0,844) en los varones y 0,785 (IC 95%: 0,748-0,817) en las mujeres.
La diferencia entre los coeficientes α aparentemente es pequeña, pero debe realizarse una comparación estadística de coeficientes α a fin de conocer si la estimación del error es estadísticamente similar entre los grupos. En este sentido, el IC95% de α1–α2 obtenido es [–0,069 a 0,088]. Ello indica que la diferencia entre ambos α no es estadísticamente significativa, pues el intervalo incluye el cero. Esto es evidencia de que el EBSE estima de forma similar el error de medida entre los 2 grupos comparados.
Este método es útil cuando se desee comparar coeficientes α de diferentes grupos y presentar la diferencia con un mayor respaldo empírico4. A su vez, evita las conclusiones derivadas del solapamiento aparente entre los IC de los α estudiados1, y brinda más información debido a que provee el rango de posibles valores del parámetro (α1–α2) bajo cierto nivel de confianza2. El lector interesado puede solicitar una sintaxis para SPSS para realizar los cálculos.
Conflicto de interesesNinguno.