Test results with and without blueprinting: Psychometric analysis using the Rasch model

Abstract

Introduction

The test blueprint bridges the teaching, learning, and assessment processes. It describes what to measure in which learning domain and at what competency level. We used Rasch analysis to compare the test results and item response patterns of two uro-reproductive tests. The Fall-2020 (Test one) exam was developed without a test blueprint, while the Fall-2021 (Test two) exam used a test blueprint.

Methods

The study analyzed data from 143 Sultan Qaboos University medical students who passed the course in fall 2020 and fall 2021. 25 MCQs were chosen at random. Psychometric analysis was performed using the Rasch model. Means, measurement errors, and reliability indices were calculated. Rasch's dichotomous model computed PCAR for unidimensionality, local item independence, person separation estimate, and fit statistics for item conformity.

Results

Both tests exhibited non-significant variations in test scores, person separation indices (PSI), and item reliability. On test two, item separation measures showed three difficulty levels. Unidimensionality assumptions were validated in both tests. Test one items 16 and 18 were 0.53 intercorrelated, indicating response dependence. Both tests produced acceptable infit statistics, with 8 items in test one and 6 in test two unfitting for the outfit range (0.7--1.3). Test two ICC had a wider range of item difficulty. The item-person map showed that students' abilities are greater than item difficulties in both tests, with a wider range of abilities in test two.

Conclusions

Psychometrically sound tests require test blueprints. The Rasch model analyzes test psychometrics effectively. Test score accuracy, item differentiation, and item independence improved with blueprinting. Creating a test with a high correlation between item difficulty and student ability reduced score measuring errors. General research should examine blueprinting methods and educational milestones.

Resumen

Introducción

El plan de pruebas une los procesos de enseñanza, aprendizaje y evaluación. Describe qué medir en qué dominio de aprendizaje y en qué nivel de competencia. Se utilizó el análisis de Rasch para comparar los resultados de las pruebas y los patrones de respuesta a ítems de dos pruebas uro-reproductivas. El examen Otoño-2020 (Prueba uno) se desarrolló sin un plan de pruebas, mientras que el examen Otoño-2021 (Prueba dos) utilizó un plan de pruebas.

Métodos

El estudio analizó datos de 143 estudiantes de medicina de la Universidad Sultan Qaboos que aprobaron el curso en el otoño de 2020 y el otoño de 2021. Se eligieron 25 MCQs al azar. El análisis psicométrico se realizó mediante el modelo de Rasch. Se calcularon medias, errores de medición e índices de confiabilidad. El modelo dicotómico de Rasch calculó la PCAR para unidimensionalidad, independencia local de ítem, estimación de separación de personas y estadísticas de ajuste para la conformidad de ítem.

Resultados

Ambas pruebas mostraron variaciones no significativas en las puntuaciones de las pruebas, índices de separación de personas (IPE) y confiabilidad de los ítems. En la prueba dos, las medidas de separación de ítems mostraron tres niveles de dificultad. Los supuestos de unidimensionalidad fueron validados en ambas pruebas. Los reactivos 16 y 18 estuvieron intercorrelacionados 0,53, indicando dependencia de la respuesta. Ambas pruebas produjeron estadísticas de infit aceptables, con 8 ítems en la prueba uno y 6 en la prueba dos no aptos para el rango de outfit (0,7--1,3). La prueba dos ICC tenía una gama más amplia de dificultad de elementos. El mapa ítem-persona mostró que las habilidades de los estudiantes son mayores que las dificultades ítem en ambas pruebas, con un rango más amplio de habilidades en la prueba dos.

Conclusiones

Las pruebas sicométricamente sólidas requieren planos de prueba. El modelo de Rasch analiza la psicometría de las pruebas de manera efectiva. La precisión de la puntuación de prueba, la diferenciación de los elementos y la independencia de los elementos mejoraron con el diseño. La creación de una prueba con una alta correlación entre la dificultad del elemento y la capacidad del estudiante redujo los errores de medición de puntuación. La investigación general debe examinar los métodos de diseño y los hitos educativos.

Introduction

The pedagogical strategies of medical education have advanced significantly in recent years, notably with the implementation of novel learning and teaching methodologies. As part of the curriculum development and improvement processes, the assessment strategy should be challenged, and medical educators should assure a well-balanced assessment that employs real, active, and authentic approaches. These comprehensive approaches emphasize the application of factual, procedural, and integrated knowledge in conjunction with the requisite skills necessary to establish competency in medical practice. Many medical schools have recently begun implementing the "assessment for learning" paradigm, in which both students and teachers are provided with information regarding how the learning process is progressing and where it needs to go, as well as the most effective way to get there. Accordingly, numerous competency-based and programmatic assessment methodologies have been implemented.¹ As proper assessment is an inherent component of medical education, a good educational process should be accompanied by an appropriate assessment strategy.

The development of a test with inadequate validity or reliability measures or with irrelevant variation among test scores is one of the major threats to an accurate assessment. Such invalid examinations devoid of objectivity could result in an inaccurate evaluation of students' knowledge or competence. Currently, the concept of validity has changed from merely criterion, content, etc. to a unified concept of construct validity, in which many sources of evidence are used to support a contention for validity, initially through Messick's framework of the five sources and, more recently, through Kane's argument-based approach to validation.² According to Cook et al., Kane's paradigm highlights four steps for valid interpretation from observation to decision making. The first step is scoring an observed performance to ensure it accurately reflects it. Second, generalize the exam outcome to test performance (Generalization). Third, real-world performance extrapolation (Extrapolation). Fourth, is decision-making based on data analysis (Implications).³

Along with these validity threats in test design, subjectivity in test papers, lack of test pre-validation by reviewers, lack of uniformity, and lengthy tests are frequently noticed problems of such poorly created tests that lack content or construct validity.⁴

Post-exam data and test scores should be evaluated using psychometric approaches to improve assessment quality. Test developers and medical educators should assess student performance reliably and consistently over time to reduce unexpected test results.⁵ Post-examination analysis improves assessment reliability and validity and reviews learning outcomes and instructional methods.^5,6 These studies help to standardize tests and to detect test items with irregular responses outside test control limits, which can lower test quality. The test psychometrics improve assessment quality in several ways: it helps to detect test items with abnormal response patterns, allowing for rewriting or rejecting of such items; it introduces new analytical methods, such as the item response theory, which interprets tests by associating student abilities with item difficulties; it improves construct, content, and concurrent test validity measures; and it improves question quality. Additionally, it allows for a more precise calculation of examiners' true scores, identification of measurement errors, reduction of inter-rater score variability, and increased test generalizability.⁷

Numerous methods have been utilized to examine and interpret post-test data in the field of test psychometrics. The classical test theory (CTT) and the more complex item response theory (IRT) have been implemented.⁷ The classical test theory is the most prevalent and widespread method. The majority of post-examination data returned to professors is derived from the CTT. It focuses primarily on assessment items and examiners' attempts to appropriately respond to these items and helps to identify the sources of measurement errors and the degrees of test score variance. In addition, a wide variety of descriptive statistics, such as the mean, standard deviations, confidence intervals of scores, skewness, kurtosis, difficulty and discrimination indices, distractor efficiency, and test overall reliability (Cronbach's alpha and Kuder Richardson measures) are provided.⁸

Despite the fact that these parameters are simple to interpret, evaluate, and provide a close look at all items and test score measures, a clearer understanding of how students interact with test items and how these items affect students' performance and behavior during the test is not described. In addition, the statistics supplied by the CTT depend on the total number of test responses, the number of test questions, and the inter-item correlation and reliability measurements. There is no evidence of the specific response pattern of each test taker to a test item or the correlations between the students' overall abilities and item difficulty. Thus, it is necessary to use a different psychometric method for test analysis that provides deeper and more intricate insights. The item response theory (IRT) helps to overcome this constraint since it gives a complete analysis of the relationship between item difficulty level and student abilities, as well as other valuable parameters such as item and person separation estimates, test unidimensionality, local item independence, differential item functioning, and item response patterns.

The logistic Rasch model for dichotomous data is one of the IRT's principal models. It establishes a logistic relationship between item difficulty and student ability (estimated based on the number of questions answered correctly); the greater the range, the greater the likelihood that a person will respond properly to a question.⁹

Common issues affecting the content and construct validity of a test include its development with underrepresented learning outcomes or an irrelevant variance (improper assessment tools). Using the test blueprint is thus a significant and typical method for ensuring a proper examination in terms of content. In addition, blueprinting ensures the test's validity. A reliable exam is consistent and capable of differentiating between good and poor students; its scores are consistent across varied testing settings.

The test blueprint provides constructive alignment between the three educational pillars (learning objectives, teaching and learning activities, and evaluation strategy). Thus, it assures assessment transparency and that students' knowledge, and skills are assessed properly using a well-defined approach.

The two-dimensional matrix (content to process matrix) design is one of the most often used methods for designing test blueprints.¹⁰ The course content areas and learning outcomes (displayed on the y-axis) are tabulated against the learning domains (cognitive, psychomotor, and affective) displayed on the x-axis using a broad sampling to ensure sufficient reliability. This approach enables an appropriate mapping of assessment to the curriculum outcomes and learning objectives. A sufficient and well-balanced sampling of course content is obtained, and design and sampling biases in examinations are minimized.

In order to develop and improve the test design and quality, the purpose of this study is to examine in detail the effect of adopting a blueprint for test design on assessment scores and item response patterns, as well as how the Rasch analysis model for psychometric evaluation of examination enables a better understanding and interpretation of exam data.

Methods

Study design

Comparative cross-sectional study was conducted to detect the differences in test results, item analysis reports and test psychometrics between two uro-reproductive course exams. Of these, the fall 2020 group, test was conducted without implementing a test blueprint (test one), while that of fall 2021 group (test two); the test was conducted with a well-constructed test blueprint. The study was conducted among phase II medical students, College of Medicine & Health Sciences Sultan Qaboos University (SQU). Phase II contains four semesters, the first of which covers advanced human anatomy and physiology. System-based courses with horizontal and vertical integration make up the last three semesters. The study involved phase II, pre-clerkship medical students, involved in one of the system-based courses (the uro-reproductive course).

Study participants

The examination committee of the College of Medicine and Health Sciences at SQU provided the study's test data. The data set was comprised of 143 uro-reproductive exam takers who passed the course's final exam. The cohort of 2020 (Group one) consisted of 72 students, of whom 32 were males (44%) and 40 were females (56%), whilst the cohort of 2021 (group two) consisted of 71 students, of which 30 were males (42%) and 41 were females (58%). Students enrolled in the course were subject to the enrollment and eligibility requirements issued by the university's Admission and Registration Deanship (A&R). Participants were exposed to comparable educational backgrounds. Except for test design with and without a test blueprint, all variables that could affect student performance were relatively constant. Both courses featured similar outcomes, instructors, educational resources, and teaching methods.

Test blueprint design

It is crucial to remember that there is no predefined test blueprint design and implementation template. However, blueprinting is a method that enables test development that adequately reflects course learning outcomes and ensures the use of an appropriate assessment tool. Therefore, the method used in this study to develop a test blueprint was the one most effective in achieving the course's learning objectives.

Steps involved in blueprint design

• 1.

  Creating a test blueprint begins with identifying the blueprint's purpose and scope.

• 2.

  Create a two-dimensional matrix listing the course's subject sections (split into themes) on the y-axis and the learning domains (levels of cognition, such as knowledge, understanding, application, etc.) on the x-axis. This ensures that all course content is covered on the final examination.

• 3.

  Determine the appropriate assessment method for each learning domain. All examination questions in this study were MCQs of type A. (for assessing the knowledge and understanding domains).

• 4.

  Determine the relative weight of each content area based on the amount of time devoted to instruction, the topic's relative value, the frequency with which it is applied in practice, and the topic's significance for subsequent learning.^11,12

• 5.

  Calculate the total number of test items by dividing the time given for the entire exam by the time allotted for each examinee to answer a single test item (time for answering a recall or a problem-solving question). In this study, the time allotted for each test was 40 minutes, the time allotted for each test item was 1.5 minutes, and students were permitted 2.5 more minutes.

• 6.

  Determine the proportional number of test items for each content area (category) based on its weight as mentioned previously. Determine the proportionate weight of each learning domain to be evaluated (knowledge, understanding, application, etc.) within each content area (topic or theme). Table 1 provides an example of the test blueprint used for test two.

  Table 1.

  Blueprint design for test two.

  Table of Specification (TOS)										Number of test Items According to Learning Domains
  No	LO/Topics	Contact Hours / Topic	Knowledge	Understanding	Application	Total number of ILOs	Knowledge	Understanding	Application	Number of Questions for each topic	Knowledge	Understanding	Application	Final Exam
  1	Anatomy	18	32	5	2	39	82%	13%	5%	6	5	1	0	5
  2	Physiology	13	52	5	0	57	91%	9%	0%	4	4	0	0	3
  3	Pathology	14	29	5	7	41	71%	12%	17%	5	3	1	1	4
  4	Biochemistry	9	23	16	4	43	53%	37%	10%	3	2	1	0	2
  5	Pharmacology	6	11	7	1	19	58%	37%	5%	2	1	1	0	2
  6	Microbiology ℑmunology	12	29	8	4	41	71%	20%	9%	4	3	1	0	3
  7	Nephrology	2	0	3	1	4	0%	75%	25%	1	0	1	0	1
  	Total	74	176	49	19	244	61%	29%	10%	25	18	5	2	25

  ILOs = Intended learning outcomes.

Importantly, the test blueprint is not used merely as a measure of test validity; rather, its combination with other measures in the context, such as post-examination reports, psychometric parameters, application utility, and expert comments, is used to generate a comprehensive understanding of assessments and apply methods for test improvement.

Study tools

Each group's uro-reproductive examination consisted of 25 multiple-choice questions picked at random from the item bank. Questions from the item bank pertinent to their item analysis reports were selected. The adequacy of test items in terms of difficulty, discrimination, and overall test reliability (Alpha value) and the reliability value if an item is omitted (Alpha without, Alpha w/o) from a test was considered.

Items with a difficulty index (P-value) within the recommended range of 30 to 70 were selected. On the basis of their discriminative efficiency (represented by r-PB, point-biserial correlation product of an individual's response to an item and the overall test response to all other items), the cut off values for selection were established as follows: >0.40 (very good); 0.20--0.29 (fairly good and needs improvement); and values ≤0.19 (poor) (removed from the item bank or revised for improvement).¹³

The test was scored only on the basis of correct responses; there were no penalties for incorrect answers. The correct response received a score of one, while the incorrect response received a score of zero. Students' overall test scores were computed, and data were expressed as mean ± standard error in measurement.

Prior to test administration, test items were reassessed based on their degree of cognitive process complexity (correspondence with the learning domains; Knowledge, comprehension, and/or application). Two raters independently rated each item. Each item was assigned a score of 1, 2, or 3 based on how well it matched the learning domains (Knowledge, understanding and application respectively) Cohen's Kappa was utilized to determine the inter-rater reliability and degree of agreement between the two raters (For nominal data that can be distinguished). The Kappa value was 0.71, and the p-value was less than 0.001, which was deemed acceptable by Cohen's cutoff.¹⁴

Item evaluation and fit statistics

The performance of test items was evaluated based on measures of difficulty and discrimination, reliability indices, Rasch model fit, test dimensionality, and degree of independence. In this study, the Rasch model analysis was conducted using the WINSTEPS analysis tool, version 5.2.3.¹⁵

The Rasch model for dichotomous data establishes a logistic relationship between individual ability and item difficulty. The greater the difference, the greater the likelihood of a correct response.⁹ We implemented only one parameter (1PL) for the IRT analysis: the item difficulty level in addition to the respondent ability trait level. Other measures, such as item discrimination and pseudo guessing, were not utilized since our test measures only one domain level of competency, namely knowledge and its application, and because all our test items consist of multiple-choice questions with simple binary responses (students are graded 0 or 1 based on their correctness).

In the Rasch model, item difficulty (P-value) is defined as the skill level required to have a 50% chance of providing the correct response. The recommended range is 30 to 70. The discrimination efficiency of a test item is its capacity to distinguish between high and low performers. The correct response must be positively discriminating.

In addition to this, as part of the Rasch analysis, the mean square indices (MNSQ) of the infit and outfit statistics for test items were calibrated. The infit MNSQ is an index sensitive to deviations in test items from the expected pattern near the difficulty mean. The outfit MNSQ is an indicator sensitive to deviations in test items among high or low difficulty outliers.¹⁶ The MNSQ is determined by dividing the test item's Chi-square statistics by their degrees of freedom.

The infit index is the more accurate of the two indices for measuring the fit of data to the Rasch model because it finds data outliers near the item characteristic curve (ICC). For the evaluation of the MNSQ overfitting and underfitting indices, respectively, (0.7 and 1.3) were utilized as respective cutoff values.¹⁷ Point-biserial correlation was used to measure the degree of correlation between the latent trait and the observed score. The link between item difficulty and individual (test-takers') performance was depicted using a Wright map, which is frequently used in the Rasch model and was calibrated in logits (Log-odd ratio).¹⁸

Test and person reliability

The Rasch analysis model examined the reliability of both tests and individuals. The reliability index (RI) quantifies the consistency of a test. It ranges between zero and one. A threshold of 0.7 is acceptable. It quantifies the proportion of test score variance attributable to error variance.¹⁹ It measures the precision of individual performance and item difficulty. Low levels of reliability are associated with high levels of Standard error of measurement (SEM).

The Rasch analysis also detects the person separation index as a reliability metric. It is an estimate of the test's ability to differentiate between individuals with different degrees of ability. According to Linacre, it runs from zero to infinity and is a ratio between the standard deviation of test-takers and their root mean square standard error.²⁰

Test unidimensionality

The Rasch analysis model was used to determine whether the test measures a single dimension. To test for unidimensionality, the principal component analysis of linearized Rasch residuals (PCAR) is performed. Residuals are defined as the difference between the observed student scores and what the Rasch model predicted.²¹

The common variance is used by PCAR to identify components in residuals. In the analysis, the raw variance unexplained by the Rasch model was employed. A contrast (component) with three or more items with unexplained variance clusters together, resulting in the creation of a subdimension in data that is distinct from the Rasch dimension. The size of the common variance of these cluster items is compared to that of the Rasch model. The bigger the difference, the greater the likelihood of component substantiality, and the assumption of test unidimensionality no longer holds. The Eigenvalue was determined for the contrasts with unexplained variance; values less than three were considered non-significant. In the Rasch analysis, this was depicted as a graph with the item difficulty measures in logits on the horizontal axis and the extracted component of linearized Rasch residuals on the vertical (Appendix A). The spread of objects throughout the whole graph and the absence of ones that stand out from the rest are considered evidence of unidimensionality.

Local item independence is another assumption of the Rasch measuring method. It is determined using the Pearson correlation analysis of linearized Rasch residuals. A value of 0.5 is considered significant and an indicator of threatening local independence.²² It can be interpreted to indicate that the probability of response to one item depends on the likelihood of response to another.

Ethical approval

After approval, test results and details of test psychometrics, including item analysis reports, were received from administrative reports. Data confidentiality was maintained throughout the study. The Medical Research Ethics Committee (MREC) of SQU approved the study's design and protocol in February 2022. (REF.NO. SQU-EC/038/2022; MREC 2686).

Results

The primary goal of this research was to identify potential differences in response patterns across two uro reproductive courses tests using the Rasch measurement model. The first exam was administered without a test blueprint, whereas the second exam was designed with a test blueprint. For each measure, the following headings will be used to present the Rasch analysis results:

Test unidimensionality

PCAR was conducted to determine the unidimensionality of the test. For both tests, the Rasch factor explained 9.10 and 11.92 (Eigenvalues) of the raw variance. The first contrast's unexplained variance was 2.66 and 2.1 for the two tests, respectively. None of the first contrast's item residuals clustered together (Values less than 3 in both tests) (Appendix A). This is verified by the observation that the variance explained by the Rasch factor is between nine and twelve times larger than the dimension recovered from the residuals. With a wider disparity in the second test (with a blueprint). Thus, the unidimensionality assumption is supported in both tests.

Local item independence

Analyses were conducted on the Pearson correlations between item standardized residuals. With an intercorrelation of 0.5, the local independence assumption is violated. In the first test, observed correlations ranged between 0.24 and 0.53, whereas in the second, all values were less than 0.35. In test one, Items 16 and 18 had an intercorrelation of 0.53; hence, the probability of responding to one of these questions is dependent on the response to the other (the local item independence assumption is violated); the sequence of these two items may influence the degree of difficulty associated with their interpretation.

Reliability and separation estimate

Item reliability coefficients were 0.87 and 0.90 for the first and second test, respectively. Item separation measures were 2.63 and 3.01 for test one and two respectively (Table 2). Person separation indices were 1.17 and 0.98 for the first and second tests, respectively.

Table 2.

Person and item reliability and separation estimate in Test one (A, without blueprint) and test two (B, with blueprint).

A: Test one (without blueprint)
Person	72 Input		72 Measured		Infit		Outfit
	Total	Count	Measure	Real SE	IMNSQ	ZSTD	OMNSQ	ZSTD
Mean	20.1	25	2.04	0.69	0.98	0.1	0.99	0.11
P. SD	3.3	−2	1.15	0.26	0.27	1.1	0.77	1
RealRMSE	0.74 True SD		0.88	Separation: 1.18*			Person Reliability:0.58*
Item	25 1nput		25 Measured		Infit		Outfit
	Total	Count	Measure	Real SE	IMNSQ	ZSTD	MNSQ	ZSTD
Mean	57.8	71.9	0	0.4	0.99	0.1	0.99	0.1
P. SD	10.7	0.3	1.18	0.13	0.11	0.7	0.42	1
Real RMSE	0.42 True SD		1.1	Separation : 2.63*			Item Reliability: 0.87*
B: Test two (with blueprint)
Person	72 Input		72 Measured		Infit		Outfit
	Total	Count	Measure	Real SE	IMNSQ	ZSTD	OMNSQ	ZSTD
Mean	19.4	25	1.88	0.64	0.99	0.1	0.98	0.2
P.SD	2.7	0	0.92	0.14	0.25	0.7	0.72	0.7
Real RMSE	0.65 True SD		0.64	Separation: 0.99*			Person reliability: 0.49*
Item	25 1nput		25 Measured		Infit		OUTFIT
	Total	Count	Measure	Real SE	IMNSQ	ZSTD	OHNSQ	ZSTD
Mean	55.8	72	0	0.44	1	0.1	0.98	1
P. SD	14.5	0	1.59	0.24	0.11	0.8	0.33	1
Real RMSE	0.5 True SD		1.51	Separation: 3.01*			Item reliability: 0.9*

Person separation index [(PSI = √ r/ (1-r)] was 1.17 and 0.98, and Person separation estimate was 1.18 and 0.99 for test one and two respectively, indicating that the test was not sensitive enough to distinguish between two groups of students with varying levels of ability. Measures of item reliability and item separation indices for tests one and two were 0.87 and 0.90, and 2.63 and 3.01, respectively, showing the presence of three distinct levels of difficulty in test two items. Values are expressed with *.

IMNSQ = Infit mean square values; OMNSQ = Outfit mean square values; ZSTD = Value of t-test; RMSE = Root mean square error (average measurement error of reported measures).

Fit of items to the Rasch model

Tables 3 and 4 depict the MNSQ indices for infit and outfit (test one and two, respectively). The infit statistics for the first test varied from 0.78 to 1.29, with a mean of (0.99 ± 0.11). All of the infit MNSQs fall within the range of 0.7 to 1.3 as indicated by Bond and Fox,³⁴ indicating that the data does not contain any unexpected responses. The average MNSQ for outfit measurements was 0.99 ± 0.42, with items 21, 19, 2, 23, 25, 5, 1, and 17 falling outside the Rasch model's acceptable fitting range. All point measure correlations (PT-measures) for test items varied from 0.17 to 0.54, with all positive values showing a correlation between test items.

Table 3.

Fit of items to the Rasch model (Fit statistics) for Test one (without blueprint).

Entry	Total	ItemDifficulty	Model	Infit		OUTFIT		PT-MEASURE		Exact match
Item	Score		S.E.	MNSQ	ZSTD	MNSQ	ZSTD	Corr.	EXOP.	OBS. %	Exp.%
Q21	67	−1.05	0.48	0.92	−0.10	2.19*	1. 57	A .23	0.23	92.9	92.9
Q19	63	−0.34	0.38	1.05	.26	1.88*	1. 70	8 .20	0.3	87.1	87.2
Q2	27	2.68	0.28	1.29	2.36	1.66*	3.13	C .20	0.47	64.3	71.5
Q23	64	−0.49	0.4	1.1	0.44	1.38*	0.86	D .17	0.28	88.6	88.6
Q7	33	2.23	0.27	1.16	1.48	1.21	1.44	E .34	0.47	65.7	69.5
Q20	61	−0.07	0.35	1.08	0.46	1.19	0.58	F .24	0.32	82.9	84.3
Q13	42	1.59	0.27	1.08	0.72	1.04	0.33	G .40	0.45	65.7	69.9
Q14	62	−0.2	0.36	1.08	0.40	1.05	0.27	H .26	0.31	85.7	85. 7
Q4	63	−. 34	0.38	1.06	0.32	1.02	.20	I .25	0.3	87.1	87.2
O18	66	−0.84	0.44	1.04	0.22	0.84	−0.08	J .24	0.25	91.4	91.4
Q8	51	0.91	0.29	1.01	0.14	0.96	−0.1	K .41	0.41	74.3	74.2
Q12	51	0.91	0.29	1.01	0.12	.9S	−0.15	L .41	0.41	77.1	74.2
Q16	69	−1.62	0.6	1.01	0.19	0.86	0.14	M .18	0.18	95. 7	95. 7
Q11	67	−1.05	0.48	1	0.12	0.92	0.11	1 .24	0.23	92.9	92.9
Q25	67	−1.27	0.53	0.99	0.12	0.63*	−0.3	k .25	0.21	94.2	94.2
Q22	60	0.05	0.34	0.97	−0.09	0.85	−0.3	j .38	0.34	81.4	83
Q5	70	−2.06	0.73	0.95	0.14	0.49*	−0.22	1 .22	0.15	97.1	97.1
Q6	53	0.74	0.29	0.93	−0.50	0.74	−1.13	h .48	0.4	75.7	75.7
O3	59	0.08	0.34	0.91	−0.43	0.7	−0.8	g .43	0.34	84.1	82.8
Q10	55	0.56	0.3	0.91	−0.55	0.88	−0.39	f .45	0.38	80	77.6
Q9	50	0.99	0.28	0.9	−0.78	−0.78	−1.09	e .51	0.42	77.1	73.5
Q24	61	−0.07	0.35	0.89	−0.50	0.82	− .35	d .41	0.32	85.7	84.3
Q1	70	−2.06	0.73	0.88	0.02	0.25*	−0.67	C .30	0.15	97.1	97.1
O15	55	0.56	0.3	0.88	−0.78	0.81	−0.67	b .48	0.38	77.1	77.6
Q17	59	0.16	0.33	0.78	−1.25	0.53*	−1.56	a .54	0.35	84.3	81.8
Mean	57.8	0	0.39	0.99	0.10	0.99	0.1			83.4	83.6
P.SD	10.7	1.18	0.13	0.11	0.71	0.42	1.01			9.4	8.6

The infit and outfit mean square statistics (MNSQ) are displayed. According to the Rasch model, values between 0.7 and 1.3 fall within the acceptable range for fitting. The infit MNSQ values show that all items fall within the acceptable range, with a mean value of 0.99 ± 0.11 SD. The average outfit MNSQ was 0.99 ± 0.42. * indicate items outside the fitting range to the Rasch model. SE = Standard error; ZSTD = Value of t-test (values between −2.00 and + 2.00 are within acceptable range to the Rasch model); PT-measure = Point-measure correlations; Obs. = observed score; Exp. = Expected score.

Table 4.

Fit of items to the Rasch model (Fit statistics) for Test two (with blueprint).

Entry	Total	Difficulty	Model	Infit		OUTFIT		PT-MEASURE		Exact match
Item	Score		S.E.	MNSQ	ZSTD	MNSQ	ZSTD	Corr.	EXP.	OBS. %	Exp.%
Q16	61	−0.1	0.34	1	0.06	1.83*	1.99	A .23	0.29	84.7	84.81
Q1	63	−0.36	0.37	1.19	0.81	1.66*	1.47	B .01	0.26	87.5	87.51
Q19	60	0.01	0.33	1.21	1.07	1.52*	1.45	C .04	0.3	83.3	83.41
Q15	35	1.94	0.26	1.31	3.01	1.39*	3.02	D .08	0.4	55.6	67.31
Q21	65	−0.66	0.41	1.09	0.4	1.22	0.58	E .13	0.24	90.3	90.31
Q22	11	3.87	0.34	1.08	0.45	1.13	0.47	F .2	0.38	86.1	85.01
Q4	71	−2.76	1.01	1.03	0.35	1.12	0.53	G .03	0.09	98.6	98.61
Q6	49	0.98	0.27	1.02	0.24	0.99	0.03	H .36	0.37	72.2	71.71
Q12	70	−2.04	0.73	1.02	0.25	0.81	0.12	I.12	0.13	97.2	97.21
Q13	71	−2.76	1.01	1.02	0.34	0.85	0.31	J .07	0.09	98.6	98.61
Q18	33	2.08	0.26	1.01	0.12	0.98	−0.09	K .40	0.4	61.1	67.61
Q3	32	2.14	0.26	0.95	−0.53	1	0.02	L .44	0.4	76.4	67.81
Q5	63	−0.36	0.37	1	0.9	0.78	−0.45	M .30	0.26	87.5	87.51
Q10	71	−2.76	1.01	1	0.32	0.51	−0.03	I.14	0.09	98.6	98.61
Q7	66	−0.84	0.44	0.97	0.81	0.99	0.17	k .25	0.22	91.7	91.71
Q9	57	0.32	0.31	0.98	−0.05	0.82	−0.58	j .37	0.32	80.6	79.31
Q23	49	0.98	0.27	0.97	−0.25	0.92	−0.4	i .41	0.37	77.8	71.71
Q2	59	0.12	0.32	0.96	−0.15	0.8	−0.58	h .37	0.31	81.9	82.01
Q8	59	0.12	0.32	0.95	−0.19	0.76	−0.71	g .39	0.31	81.9	82.01
Q11	67	−1.05	0.48	0.94	−0.05	0.79	0.18	f .28	0.2	93.1	93.11
Q26	68	−1.3	0.53	0.93	−0.02	0.49	−0.69	e .31	0.18	94.4	94.51
Q25	58	0.22	0.32	0.88	−0.65	0.81	−0.6	d .44	0.32	81.9	80.71
Q14	54	0.59	0.29	0.86	−0.98	0.76	−1.02	c.5	0.35	81.9	75.91
Q24	47	1.13	0.27	0.86	−1.29	0.84	−0.97	b .52	0.38	79.2	70.61
Q17	55	0.5	0.3	0.83	−1.2	0.68*	−1.4	a.53	0.34	81.9	77
Mean	55.8	72	0.43	1	0.09	0.98	0.1			84.2	83.41
P. SD.	14.5	0	0.24	0.11	0.81	0.33	0.991			10.5	10.1

The infit and outfit mean square statistics (MNSQ) are displayed. According to the Rasch model, values between 0.7 and 1.3 fall within the acceptable range for fitting. The infit MNSQ values show that all items fall within the acceptable range, with a mean value of 1.00 ± 0.11 SD. The average outfit MNSQ was 0.98 ± 0.33. * indicate items outside the fitting range to the Rasch model. SE = Standard error; ZSTD = Value of t-test (values between −2 and + 2 are within acceptable range to the Rasch model); PT-measure = Point-measure correlations; Obs. = observed score; Exp. = Expected score.

Table 4 displays the test two item fit characteristics to the Rasch model. The infit MNSQ values demonstrate that all items fall within the acceptable range, with a mean value of 1 ± 0.11 SD. Numerous test items (16,21,22,4,6,12,13,18,5, and 10) exhibit MNSQ values around or equal to 1.0, indicating an excellent fit of test items to the Rasch model with few unexpected response patterns.

The average outfit MNSQ was 0.98 ± 0.33, with items 16, 1, 19, 15, and 17 falling outside of the Rasch model's acceptable ranges. These items had unexpected response patterns and did not support the test's underlying construct.

Participants with unexpected responses

The item's observed score and the score predicted by the Rasch model were analyzed. The findings of test one indicate the occurrence of 21 items with unexpected responses, with item two being the most frequent (6 unexpected responses). Whether, on test two, 19 questions have unexpected responses, with item one occurring most frequently (6 unexpected responses).

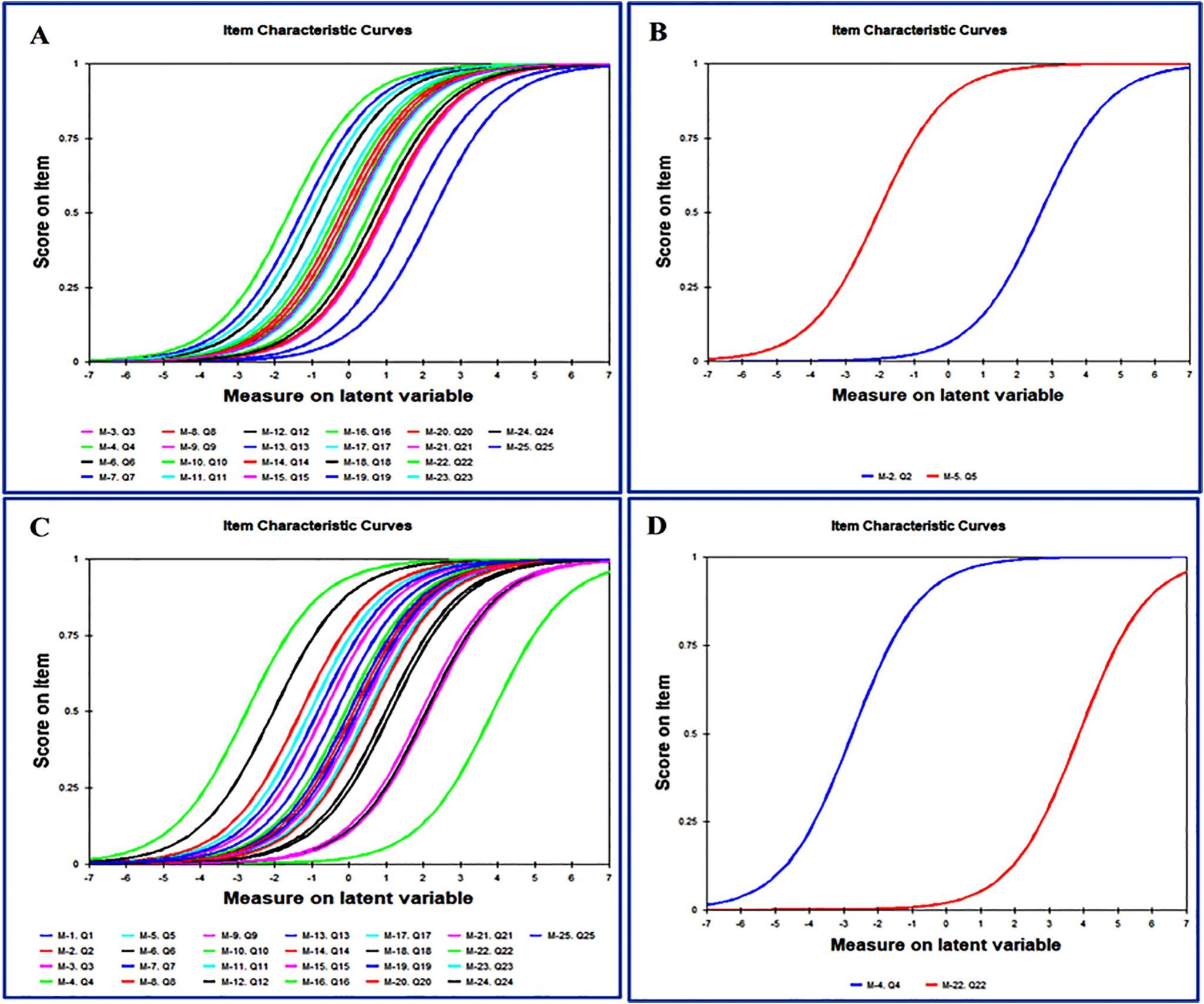
Item characteristic curve

Fig. 1 illustrates the item characteristic curve for the entire examination, as well as the curves for the easiest and most difficult questions separately.

Fig. 1.

Item characteristic curve. A and C: entire test. B and D: for test one and two's easiest and difficult items. Test one's most difficult and easiest questions are 2 and 5, with 2.68 and −2.06 logits, respectively (B component of the fig.). Question 22 and 4 are the difficult and easiest items in test two (D component of the fig.) with 3.87 and −2.76 logits, respectively. As seen by the curves, test two has a wider range of item difficulty measures.

The range of item difficulty measures in test two is broader than in test one. Questions 2 and 5 on test one have the lowest and highest logit degrees of difficulty, respectively. Questions 22 and 4 in the test two are the most difficult and easiest, respectively (Fig. 1, B and D).

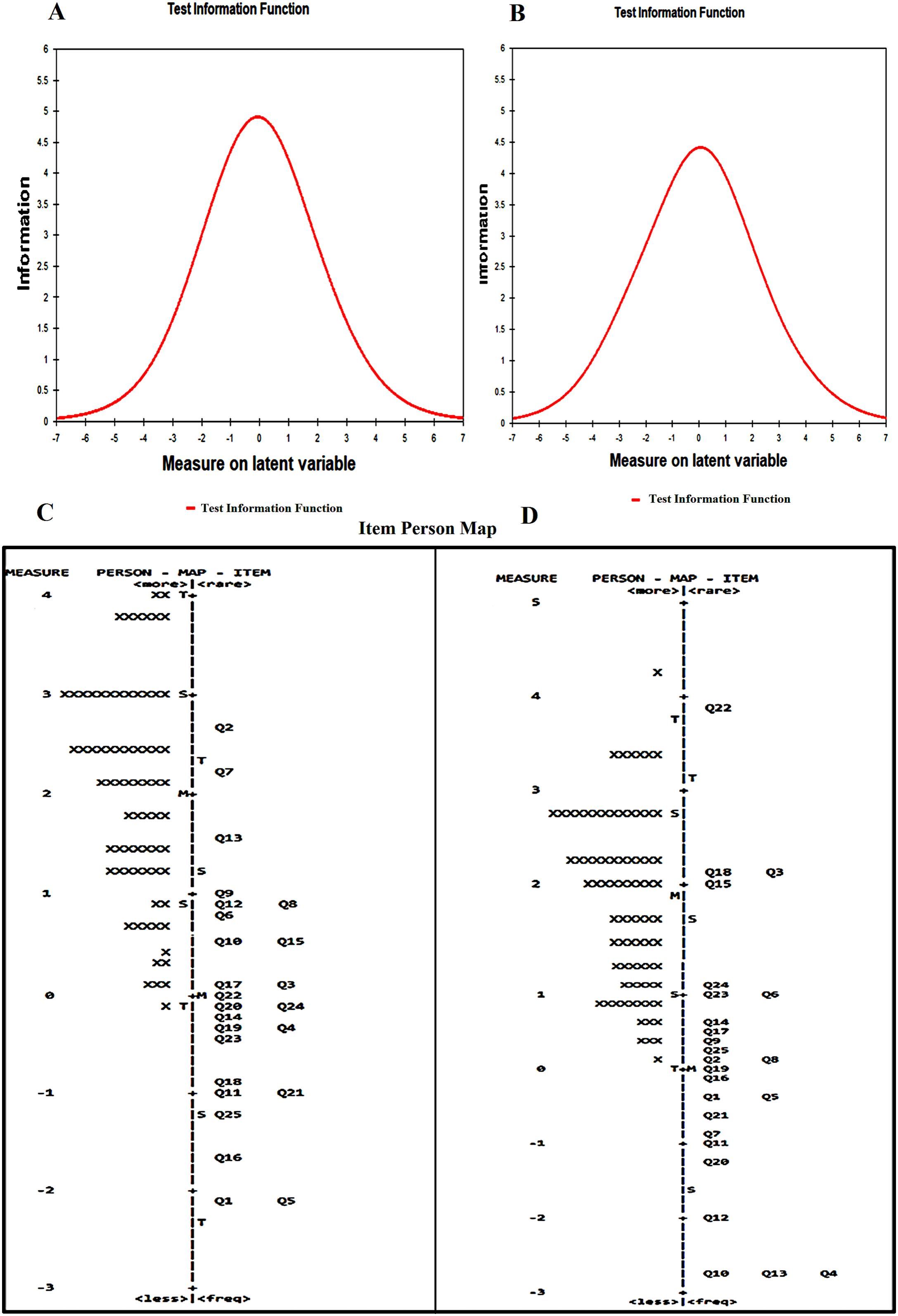
Test information function

Fig. 2 depicts the relevant test information values for the first and second tests. The test information curve is the sum of item information measures (reliability indices) at different student ability levels (measured in logits). According to both curves, students with low and high abilities have low levels of effective test measurement values, whilst students with average abilities (zero logits) demonstrate the highest levels of effective test measurement values.

Fig. 2.

Test information function (TIF), (A and B for test one and two), and Item-person map (C and D for test one and two). In A and B, as inferred from both curves, students with low and high abilities have low levels of effective test measurement values, whilst students with average abilities (zero logits) demonstrate the highest levels of effective test measurement values. Test two has a slightly broader curve as well as a broader range of effective measurements across test takers. Whereas, In C and D, the abilities of the students are presented in relation to the item difficulty for tests one and two. In both tests, students' abilities (measured in logits) are greater than item difficulties, with a wider range of abilities among group 2 test-takers (1.88 ± 0.92 on average, with a maximum of 4.27). Each X stands for two students. The values on the left show students' abilities and item difficulty in logits (from −3 to 5). M represents the mean; S and T are one and two standard deviations (SD) distant from the mean, respectively.

Item-person map

Fig. 2 (C and D) exhibits concurrent item-person map. In log-odd units, the values on the graph's left side represent students' abilities and item difficulties (logits from −3 to 5). M represents the mean, whereas S and T are separated from the mean by one and two standard deviations (SD), respectively. Exam questions range from basic (at the bottom) to difficult (at the top), and test-takers range from poor performers (at the bottom) to high performers (at the top).

The map demonstrates that test two questions cover a wider range of difficulty, from −2.76 to 3.87 logits (with a mean of 0.00 ± 1.59). While the item difficulty measurements for test one vary from −2.06 to 2.68 logits (with a mean of 0.00 ± 1.18).

A person's ability is measured on a scale ranging from −0.12 to 5.11 logits (with a mean of 2.04 ± 1.15) on the first test. On the second test (with blueprint), students' abilities range from 0.12 to 4.27 logits on average, with a standard deviation of 0.88 logits.

Besides, as shown in Fig. 2, student ability exceeds item difficulty on both examinations; hence, students are more likely to correctly respond to questions.

Some test items with difficulty measures are below the student with the lowest ability on both exams, but none is above the student with the highest ability. In both examinations, the majority of questions and test-takers cluster around their respective means.

In addition, there are more gaps in the item hierarchy of test one and items vary in their level of difficulty when compared to test two items; the majority of test items are placed on the easier portion of the map, away from where students' abilities are located.

Discussion

Assessment plays a crucial part in the medical school curriculum because it provides a way of assessing student progress toward the desired learning outcomes. To ensure that assessments are aligned with course goals and address important learning outcomes in a balanced manner, it is imperative that they are designed according to a well-considered approach.²³

Validity, reliability, and efficiency (within the limitations of time, cost, and number of students) are the attributes of an effective assessment.²⁴ Multiple variables can influence a test's validity and reliability; nevertheless, construct underrepresentation and construct-irrelevant variance are two of the biggest concerns in terms of validity. Therefore, these significant test-related threats may be mitigated with a well-constructed test blueprint. It addresses the expected level of competency in each learning domain and the precise measures to be used to evaluate the progress.²⁵

In order to enhance and improve the test design and quality, the purpose of this study was to examine in detail the effect of using a blueprint for test design on assessment scores and item response measures, as well as how the Rasch analysis model for psychometric evaluation of examination enables a better understanding and interpretation of exam data.

The dimensionality of a test was evaluated using the Rasch model's principal component analysis of residuals (PCAR).²¹ This was the initial phase of analyzing exam data. This indicates whether the test assesses a single construct (cognitive or a psychomotor ability). The Rasch factor analysis (raw variance explained by the Rasch model) for the first test (without blueprint) and the second test (with blueprint) yielded the values 9.2 and 11.92, respectively (Eigenvalue units). After removing the data contributing to this factor and examining the residuals, the initial comparison between the two groups revealed values of 2.66 and 2.21, in the first contrast respectively. Therefore, since the observed values in the first contrast are less than 3, it may be concluded that items in this dimension did not support a single underlying construct, and test unidimensionality was supported in both groups. Linacre described this.²⁰ By revising these items in the first contrast for both tests, non-meaningful differences were discovered in terms of item content. This suggests that discrepancies in responses to these test items may have been the result of chance. Unidimensionality was supported in both knowledge-based assessments.

Local item independence was also determined by measuring the Pearson correlation of linearized Rasch residuals. Fan and Bond stated that test unidimensionality is closely connected with item dependency and could be determined by analyzing the Rasch model residuals.²⁶

In this study, it was determined that the inter-item correlations in the second test (with blueprint) were all less than 0.35, however in the first test (without blueprint), items 16 and 18 have a 0.53 intercorrelation, indicating that responses to one item depend on responses to the other. Accordingly, it may be inferred that all questions on the second test were locally independent and that discrepancies in item responses were due to differences in the trait being measured. This is consistent with Cohen and Sweedik's findings.²⁷ However, in the first test, two items exhibited significant intercorrelation scores, indicating that the chance of responding to one item depends on the other. Therefore, both questions were necessary for the exam. As stated by Aryadost and his colleagues, local independence among test items might contribute to bias in assessing person and item parameters.²⁸ Consequently, blueprinting improved the degree of item independence in the test.

Using Rasch analysis, both item and student reliability measures were determined. As there is a relationship between the student's ability and the item's difficulty, numerous values could be reported.

The item reliability coefficients for the first and second tests were 0.87 and 0.90, indicating that 87% and 90% of the variation among test measures is a reliable variance and that only 13% and 10% of the variance in test one and test two is attributed to measurement errors, respectively. The item separation values for tests one and two were 2.63 and 3.01, respectively, showing three distinct degrees of difficulty among the second test's items (with a blueprint). Consequently, it may be inferred that a well-designed test blueprint produced test items with a greater degree of difficulty level variation. These findings align with those of Gill and Sen, who found that a test blueprint facilitates the alignment of assessment and learning objectives. It assists in overcoming the primary threats of a test, which include test designs with insufficiently sampled content or structures with irrelevant and biased content, which may be dependent on the bias of the paper's setter and the affinity for specific themes and topics.²⁹

Person separation indices for the first and second tests were 1.17 and 0.98, respectively, showing that neither test was sensitive enough to distinguish between two groups of students with different levels of performance (abilities relative to test items). This was noted by Bond and Fox, who said that the greater the PSI score (> 2), the more distinct the student cohort may be.¹⁸ Our findings may have been attributable to the small number of test items (25 items) and the fact that each question assessed the same construct (knowledge-based assessments). Similarly, it was observed that in certain instances, low-ability test takers prefer to randomly guess the correct response, and this data suggests that items with a high ability to differentiate may not function well for the subgroup that prefers to reply to questions by guessing. This is consistent with the findings of Aryadoust et al., who discovered that students who answer questions by guessing might skew test results because they tend to take greater risks when confronted with a challenge or difficulty.²⁸

For each test item, the infit and outfit mean square indices (MNSQ) were calculated. They evaluate the fit of the data to the Rasch model, i.e., how student ability and item difficulty tend to assess the same construct.¹⁷ According to Linacre, the infit MNSQ is an inlier sensitive index that measures unexpected responses to test items that are close to the student's average ability level, while the outfit statistics is an outlier sensitive index that measures the unusual observed data of students' responses that are far from the student's average ability level (too easy and too difficult items).¹⁷

It was found that in test one (without blueprint), the infit MNSQ results indicate that all items fall within the acceptable range, with a mean value of 0.99 logits ± 0.11 standard deviations (SD). The outfit MNSQ was 0.99 ± 0.42 logits, with items 21, 19, 2, 23, 25, 5, 1, and 17 above the Rasch model's fitting limit (Table 3). However, in test two, the infit MNSQ values indicate that all items fall within the acceptable range (0.7-1.3), with a mean value of 1 ± 0.11 SD. The average outfit MNSQ was 0.98 ± 0.33, with items 16, 1, 19, 15 and 17 not fitting the Rasch model.

Based on these results, it can be concluded that a well-designed test blueprint improved the Rasch model fit of items in the second test. Only five items go outside the outfit range, with values between 0.68 and 1.83 (corresponding to a 47% and 45% larger and smaller divergence in the observed score, respectively, than predicted by the model) (degree of noise). In addition, as indicated by Wright and Linacre, this noise raises the measurement standard error.²²

In the first test (without a blueprint), eight items were found outside the expected outfit range, with values ranging from 2.19 to 0.53 (representing a 54% and 88% deviation in the observed score, respectively, from the model's prediction). Consequently, these items have a higher level of noise. Hence, the test reveals a greater number of measurement errors. These items beyond the fitting range must be explored since they did not support the test's underlying construct. These items show an unexpected variation in test scores that may be attributable to guessing. This is consistent with Wright and Linacre's assertion that test items tend to overfit the Rasch model when many high-ability test-takers and few low-ability test-takers likely to answer the question correctly, and underfit the Rasch model when the opposite happens.²²

A blueprint provided improved alignment and development of a test and helped exam content validation by ensuring that test scores were relevant to the topic of interest. This was confirmed by the improved fit of test two items to the Rasch model with limited noise and measurement errors compared to test one (without blueprinting). Examining the item characteristic curve allowed for a comparison of the test's easy and difficult questions (Fig. 1). The ICC displays the probability that a student will answer a question correctly as a function of item difficulty and student ability.⁴¹

The range of item difficulty was broader on test two (from −2.76 to 3.87) than on test one (from −2.06 to 2.68), with averages of 0.00 ± 1.59 and 0.00 ± 1.18 logits for tests two and one, respectively. Broader range of item difficulty measures in test two (with blueprinting) shows a better construction of test items with a more reliable degree of variance among test scores.

Based on the curves. It may be concluded that students with average ability (0.00 logits) on test two are more likely to answer questions with the same degree of difficulty on test one. Therefore, blueprinting improves the overall performance of students on tests. The probabilities deduced from the ICC can be employed in future standard-setting studies to enhance the accuracy and reliability of pass marks and cut-off grades. This is consistent with what Tavakol and Dennick stated in their work titled "Psychometric evaluation of a knowledge-based examination using Rasch analysis: an illustrative guide".⁷

Fig. 2 (A and B) displays the test information function (sum of effective test measurement values) for both tests one and two. These graphs demonstrate the relationship between the abilities of students (measured in logits) and the sum of the test information measures (index of test reliability and effective variance among test scores). These fig.s indicate that both exams have lower levels of reliability among students with high and low levels of ability. In addition, it may be inferred that curve two (representing test two with blueprint) shows a broader range of effective measurements among test takers. Thus, test two demonstrates better reliability and effective test measures when evaluating students with varying levels of ability than test one (without blueprint).

Finally, the item person map was displayed in Fig. 2 (C and D). It gives a visual and quantitative representation of the relationship between item difficulty and student ability.⁷ It presents a comparison between the student's ability and the item's difficulty, indicating whether the item is easier or more difficult than the student's ability. According to Tavakol and Dennick, a perfect test that conforms to the Rasch model is one in which both item difficulty and student ability are centered around an average of 0.00 logits.⁷

In this study, it was found that the range of item difficulty on test two is from −2.76 to 3.87 logits, with a mean of 0.00 ± 1.59, whereas on test one, the range was from −2.06 to 2.68 logits, with a mean of 0.00 ± 1.18. Thus, it may be concluded that the second test's standard deviation and item difficulty spread were greater than the first. This distribution allows the assessment of students with differing levels of ability.

For the first test, student ability was measured on a scale ranging from −0.12 to 5.11 logits (with a mean of 2.04 ± 1.15). In the second test (with blueprint), students’ abilities range from 0.12 to 4.27 logits with a mean of 1.88 ± 0.91. It may be deduced that test one is less difficult than test two.

According to the map, the majority of test one items are placed between −1.18 and 1.18 logits (SD), whereas test two items are located between −1.59 and 1.59 logits. The majority of test one and test two ability scores fell between the ranges of −1.15 to 1.15 and −0.91 to 0.91 logits, respectively. Consequently, the standard deviation and distribution of item difficulty are larger than the standard deviation and distribution of student ability for both tests, with the difference being more evident on test two. As a result, it can be concluded that the distribution of test items is not as optimal as it should be, given that a large proportion of test items are on the easier end of the scale (1 and 2 ± SD from the mean), with the number of easy items being more frequent in test one (without blueprint).

Further, compared to test two, a greater number of gaps were seen in the item difficulty hierarchy in test one (fig. 2). As a result, there are inadequate items to evaluate the various abilities of test-takers, especially at one standard deviation from the mean, where the majority of test-takers are placed. In context of this, creating a test with a carefully thought-out test blueprint allowed for a more constructive alignment of the test with the course learning outcomes, increased the test's construct and content validity,³⁰ and therefore allowed for a better fit of the test items to the Rasch model when considering the item difficulty and student ability levels.

A number of limitations should be addressed while reporting this work. First, every assessment has an intrinsic measurement error, which may influence its outcomes. Due to the rigorous entry criteria, medical students are inherently strong achievers; consequently, they may compensate for any intervention through their own motivations, character traits, and academic abilities. Third, the inherent or latent variables such as academic abilities, gender, and IQ (Intelligence quotient) level that might influence test performance were not measured, which could be a disadvantage. Fourth, the number of test items is relatively low; this was determined by the number of topics and learning outcomes; a test blueprint was created based on this; learning outcomes and the percentage of each learning domain (Knowledge, understanding, and application) were measured; and the test was created accordingly. In addition, in the analysis based on the IRT and Rasch model, test items are evaluated individually and student answers to each item are assessed. This varies from the traditional analysis based on the CTT, in which the overall response to the entire test is measured, with the number of test items dictating the measurement. Numerous approaches for blueprinting are utilized (either content-oriented or process-oriented), and in this study, the content-by-process matrix was employed to incorporate these two ways into a single framework. A different way of blueprinting may affect the results. Lastly, notwithstanding the relevance of our findings, the application of blueprinting and the adoption of the Rasch model for analysis need to be applied to a larger number of courses and other medical institutions in order to generalize the results.

With the development of the new competency-based curriculum, assessment has become an integral aspect of medical education. Thus, it goes much beyond only testing the students' knowledge to the extent that it also enhances their professionalism and competence. When developing a test, it is crucial to ensure that the method and type of assessment are appropriate for the entire curriculum. Alignment between the test's content and the learning curriculum is a crucial part of test validity. Currently, a test blueprint is an integral part of assessment, significantly enhancing the content and construct validity of a test. It specifies what to assess, the learning domain, and the appropriate test modality. In addition to its role in test content validation, it serves as a tool for enhancing teaching effectiveness and promotes curriculum mapping.

The Rasch model is an effective analysis tool that goes beyond classical test theory to determine the correlation between item difficulty and student ability. A psychometrically sound test that fits the Rasch model should be reliable, unidimensional, differentiating, have a high degree of item independence, and have item measures that fit the Rasch model well. In the current study, the adoption of a test blueprint enhanced the accuracy of test scores, the test's ability to differentiate, and the degree of local item independence. Creating a test with a high degree of correlation between the students' abilities and the level of difficulty of the test items using a test blueprint assists in minimizing the extent of measurement errors. Different blueprint design matrices and their usage in various tests, as well as the employment of the Rasch model for psychometric analysis in tests that do not merely assess the knowledge domain, require additional investigation.

Funding

The research was not specifically funded.

Ethical approval

After approval, test results and details of test psychometrics, including item analysis reports, were received from administrative reports. Data confidentiality was maintained throughout the study. The Medical Research Ethics Committee (MREC) of Sultan Qaboos University approved the study's design and protocol in February 2022. (REF.NO. SQU-EC/038/2022; MREC 2686).

ORCID: Hussein Abdellatif: https://orcid.org/my-orcid?orcid=0000-0001-5590-5112

Disclosure statement

Author declared no potential conflicts of interest.